Angenommene Kenntnisse
Die Studierenden werden in früheren Jahren umfangreiche informelle Erfahrungen mit Geometrie gesammelt haben, und dies wird eine gute intuitive Grundlage für den systematischeren Ansatz zur Geometrie bieten, der in den Jahren 7-10 angemessen ist. Die besonderen Themen aus den Jahren F−6, die für dieses Modul relevant sind, sind:
- Die Verwendung von Kompassen und Linealen und das sorgfältige Zeichnen geometrischer Figuren.
- Arten von Winkeln, einschließlich mindestens rechter Winkel, spitzer Winkel, stumpfer Winkel und
Reflexwinkel. - Dreiecke, einschließlich einer informellen Einführung in gleichschenklige und gleichseitige Dreiecke.
- Quadrilaterals, einschließlich einer informellen Einführung in Quadrate, Rechtecke, Parallelogramme, Trapeze und Rauten.
- Informelle Erfahrung mit Translationen, Reflexionen, Rotationen und Vergrößerungen,
und mit Symmetrie im Rahmen von Aktivitäten wie dem Falten eines gleichschenkligen Dreiecks, Rechtecks oder einer Raute.
Motivation
 Geometrie wird verwendet, um die Welt um uns herum zu modellieren. Ein Blick auf die Dächer von Häusern zeigt Dreiecke, Trapeze und Rechtecke, während Fliesenmuster in Bürgersteigen und Bädern Sechsecke, Fünfecke, Dreiecke und Quadrate verwenden.
Geometrie wird verwendet, um die Welt um uns herum zu modellieren. Ein Blick auf die Dächer von Häusern zeigt Dreiecke, Trapeze und Rechtecke, während Fliesenmuster in Bürgersteigen und Bädern Sechsecke, Fünfecke, Dreiecke und Quadrate verwenden.
Bauherren, Fliesenleger, Architekten, Grafikdesigner und Webdesigner verwenden routinemäßig geometrische Ideen in ihrer Arbeit. Die Klassifizierung solcher geometrischen Objekte und die Untersuchung ihrer Eigenschaften sind sehr wichtig. Geometrie hat auch viele Anwendungen in der Kunst.
So wie die Arithmetik Zahlen als grundlegende Lernobjekte hat, sind Punkte, Linien und Kreise die Grundbausteine der ebenen Geometrie.
In der Geometrie der Sekundarstufe beginnen wir mit einer Reihe intuitiver Ideen (Punkte, Linien und Winkel), die überhaupt nicht leicht genau zu definieren sind, gefolgt von einigen Definitionen (vertikal entgegengesetzte Winkel, parallele Linien usw.) und daraus leiten wir wichtige Fakten ab, die oft als Theoreme bezeichnet werden. In der Sekundarstufe sollte sich das Niveau der Strenge von Jahr zu Jahr langsam entwickeln, aber in jeder Phase ist eine klare Festlegung sehr wichtig und sollte betont werden.
So bietet die Geometrie den Schülern die Möglichkeit, ihre geometrische Intuition zu entwickeln, die in vielen Lebensbereichen Anwendung findet, und auch zu lernen, logische Argumente zu konstruieren und Schlussfolgerungen in einer Umgebung zu ziehen, die größtenteils unabhängig ist
der Zahl.
Inhalt
Punkte und Linien
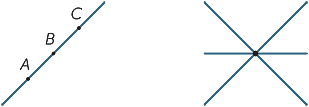
Die einfachsten Objekte in der ebenen Geometrie sind Punkte und Linien. Da sie so einfach sind, ist es schwierig, sie genau zu definieren, stattdessen möchten wir den Schülern eine grobe Beschreibung ihrer Eigenschaften geben, die unserer Intuition entspricht. Ein Punkt markiert eine Position, hat aber keine Größe. In der Praxis hat ein Punkt, wenn wir ihn zeichnen, eindeutig eine bestimmte Breite, aber er repräsentiert einen Punkt in unserer Vorstellung. Eine Linie hat keine Breite und erstreckt sich unendlich in beide Richtungen. Wenn wir eine Linie zeichnen, hat sie Breite und Enden, also ist sie nicht wirklich eine Linie, sondern stellt eine Linie in unserer Vorstellung dar. Bei zwei verschiedenen Punkten A und B gibt es eine (und nur eine) Linie, die durch beide Punkte verläuft. Wir verwenden Großbuchstaben, um auf Punkte zu verweisen und Linien zu benennen, indem wir entweder zwei Punkte auf der Linie angeben oder Kleinbuchstaben wie  und m . Daher wird die unten angegebene Zeile als Linie AB oder als Linie
und m . Daher wird die unten angegebene Zeile als Linie AB oder als Linie  .
.

Bei zwei verschiedenen Linien gibt es zwei Möglichkeiten: Sie können sich entweder an einem einzigen Punkt treffen oder sie können sich nie treffen, egal wie weit sie verlängert (oder produziert) sind. Linien, die sich nie treffen, werden als parallel bezeichnet. Im zweiten Diagramm schreiben wir AB //CD.
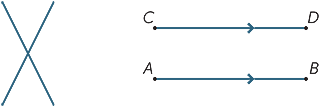
Drei (oder mehr) Punkte, die auf einer geraden Linie liegen, werden als kollinear bezeichnet.
Drei (oder mehr) Linien, die sich an einem einzigen Punkt treffen, werden als gleichzeitig bezeichnet.
|
|
|
| Kollinear |
Gleichzeitig |
Übung 1
Zeichnen Sie drei Linien, die nicht gleichzeitig sind, sodass keine zwei parallel sind.
Übung 2
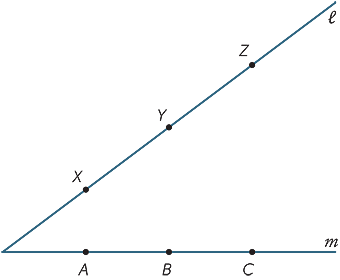
Machen Sie eine große Kopie des Diagramms unten. Die Punkte X, Y, Z sind beliebige Punkte auf der Linie  und A, B, C sind beliebige Punkte auf der Linie m. Join AY und XB nennen ihren Schnittpunkt R. Join BZ und YC und nennen ihren Schnittpunkt P. Join CX und ZA und nennen ihren Schnittpunkt Q. Was fällt Ihnen an den Punkten P, Q, R auf? (Dieses Ergebnis nennt man Pappus ‚Theorem, c. 340 AD.)
und A, B, C sind beliebige Punkte auf der Linie m. Join AY und XB nennen ihren Schnittpunkt R. Join BZ und YC und nennen ihren Schnittpunkt P. Join CX und ZA und nennen ihren Schnittpunkt Q. Was fällt Ihnen an den Punkten P, Q, R auf? (Dieses Ergebnis nennt man Pappus ‚Theorem, c. 340 AD.)
Intervalle, Strahlen und Winkel
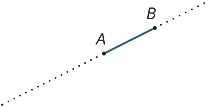 Angenommen, A und B sind zwei Punkte auf einer Linie. Das Intervall
Angenommen, A und B sind zwei Punkte auf einer Linie. Das Intervall
AB ist der Teil der Linie zwischen A und B, einschließlich der beiden Endpunkte.
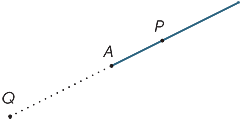 Der Punkt A im Diagramm teilt die Linie in zwei Teile, die Strahlen genannt werden. Der Strahl AP ist der Strahl, der den Punkt P (und den Punkt A) enthält.
Der Punkt A im Diagramm teilt die Linie in zwei Teile, die Strahlen genannt werden. Der Strahl AP ist der Strahl, der den Punkt P (und den Punkt A) enthält.
Winkel
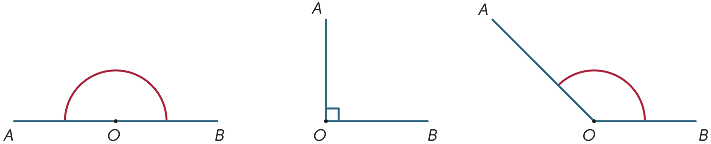
 Im Diagramm wird der schattierte Bereich zwischen den Strahlen OA und OB als Winkel AOB oder Winkel BOA bezeichnet. Das Winkelzeichen
Im Diagramm wird der schattierte Bereich zwischen den Strahlen OA und OB als Winkel AOB oder Winkel BOA bezeichnet. Das Winkelzeichen ![]() wird geschrieben, also schreiben wir
wird geschrieben, also schreiben wir ![]() AOB.
AOB.
 Der schattierte Bereich außerhalb wird als Reflexwinkel bezeichnet, der durch OA und OB gebildet wird. Meistens beziehen sich alle unsere Winkel auf den Bereich zwischen den Strahlen und nicht außerhalb, es sei denn, wir geben das Wort Reflex an.
Der schattierte Bereich außerhalb wird als Reflexwinkel bezeichnet, der durch OA und OB gebildet wird. Meistens beziehen sich alle unsere Winkel auf den Bereich zwischen den Strahlen und nicht außerhalb, es sei denn, wir geben das Wort Reflex an.
Die Größe eines Winkels
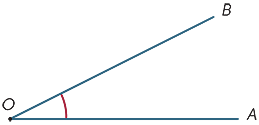 Stellen Sie sich vor, dass der Strahl OB um den Punkt O gedreht wird, bis er entlang OA liegt. Das Ausmaß der Drehung wird als Größe des Winkels AOB bezeichnet. In ähnlicher Weise können wir die Größe des Reflexwinkels definieren.
Stellen Sie sich vor, dass der Strahl OB um den Punkt O gedreht wird, bis er entlang OA liegt. Das Ausmaß der Drehung wird als Größe des Winkels AOB bezeichnet. In ähnlicher Weise können wir die Größe des Reflexwinkels definieren.
Wir werden oft kleine griechische Buchstaben verwenden, α, β, γ, … um die Größe eines Winkels darzustellen.
Die Größe des Winkels, der einer vollen Umdrehung entspricht, wurde (von den Babyloniern) in 360 gleiche Teile geteilt, die wir Grad nennen. (Sie wählten wahrscheinlich 360, da es in der Nähe der Anzahl der Tage in einem Jahr war.) Daher beträgt die Größe eines geraden Winkels 180 ° und die Größe eines rechten Winkels 90 °. Andere Winkel können (ungefähr) mit einem Winkelmesser gemessen werden.
|
|
||
| Gerader Winkel | Rechter Winkel |
Stumpfer Winkel |
Winkel werden nach ihrer Größe klassifiziert. Wir sagen, dass ein Winkel mit der Größe α akut
(ein Wort, das ’scharf‘ bedeutet) ist, wenn 0° < α < 90°, α stumpf (ein Wort, das ’stumpf‘ bedeutet) ist, wenn
90° < α < 180° und α Reflex ist, wenn 180 ° < α < 360 °.
Da der Winkelmesser zwei Skalen hat, müssen die Schüler beim Zeichnen vorsichtig sein und
Winkel messen. Es ist eine lohnende Übung, einen Winkelmesser zu verwenden, um einige Winkel zu zeichnen, wie zum Beispiel 30°, 78°, 130°, 163°.
Übung 3
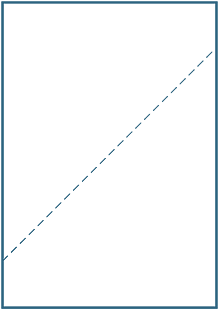 Falten Sie ein A4-Blatt Papier passend zu den (diagonal) gegenüberliegenden Ecken. Zeichnen Sie eine Linie entlang der gebildeten Falte und messen Sie die Winkel zwischen der Falte und der Seite.
Falten Sie ein A4-Blatt Papier passend zu den (diagonal) gegenüberliegenden Ecken. Zeichnen Sie eine Linie entlang der gebildeten Falte und messen Sie die Winkel zwischen der Falte und der Seite.
In der obigen Übung bilden die beiden Winkel zusammen eine gerade Linie und addieren sich so zu 180°. Zwei Winkel, die sich zu 180 ° addieren, werden als Ergänzungswinkel bezeichnet; Somit sind 45 ° und 135 ° Ergänzungswinkel.
Zwei Winkel, die sich zu 90 ° addieren, werden als komplementär bezeichnet; Somit sind 23 ° und 67 °
komplementäre Winkel.
Winkel an einem Punkt
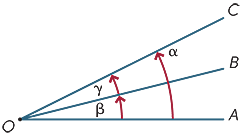 Zwei Winkel an einem Punkt sollen benachbart sein, wenn sie einen gemeinsamen Strahl teilen. Daher sind im Diagramm
Zwei Winkel an einem Punkt sollen benachbart sein, wenn sie einen gemeinsamen Strahl teilen. Daher sind im Diagramm ![]() AOB und
AOB und ![]() BOC benachbart.
BOC benachbart.
Benachbarte Winkel können hinzugefügt werden, also im Diagramm
α = β + γ.
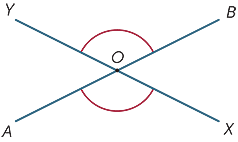
Wenn sich zwei Linien schneiden, werden am Schnittpunkt vier Winkel gebildet.
Im Diagramm werden die mit ![]() AOX und
AOX und ![]() BOY gekennzeichneten Winkel als vertikal gegenüberliegend bezeichnet.
BOY gekennzeichneten Winkel als vertikal gegenüberliegend bezeichnet.
 Seit
Seit
-
 AOX ist die Ergänzung von
AOX ist die Ergänzung von  BOX (gerader Winkel).
BOX (gerader Winkel). -
 JUNGE ist auch die ergänzung von
JUNGE ist auch die ergänzung von  BOX (gerade winkel),
BOX (gerade winkel),
wir können daraus schließen, dass diese vertikal entgegengesetzten Winkel ![]() AOX und
AOX und ![]() BOY gleich sind. Wir haben also unsere erste
BOY gleich sind. Wir haben also unsere erste
wichtige geometrische Aussage:
Vertikal entgegengesetzte Winkel sind gleich.
Ein Ergebnis in der Geometrie (und in der Mathematik im Allgemeinen) wird oft als Satz bezeichnet. Ein Satz ist eine wichtige Aussage, die durch logische Deduktion bewiesen werden kann. Das obige Argument ist ein Beweis für den Satz; Manchmal werden Beweise formell nach der Aussage des Satzes präsentiert.
 Wenn sich zwei Linien so schneiden, dass alle vier Winkel rechtwinklig sind, werden die Linien als senkrecht bezeichnet.
Wenn sich zwei Linien so schneiden, dass alle vier Winkel rechtwinklig sind, werden die Linien als senkrecht bezeichnet.
Winkel an einem Punkt – Geometrische Argumente
Die folgenden Gründe können in geometrischen Argumenten verwendet werden:
- Benachbarte Winkel können addiert oder subtrahiert werden.
- Winkel in einer Umdrehung addieren sich zu 360 °.
- Winkel in einer geraden Linie addieren sich zu 180 °.
- Vertikal entgegengesetzte Winkel sind gleich.
Transversen und parallele Linien
 Eine Querlinie ist eine Linie, die auf zwei andere Linien trifft.
Eine Querlinie ist eine Linie, die auf zwei andere Linien trifft.
Entsprechende Winkel
Verschiedene Winkel werden durch die Transversale gebildet. In den folgenden Diagrammen werden die beiden markierten Winkel als entsprechende Winkel bezeichnet.
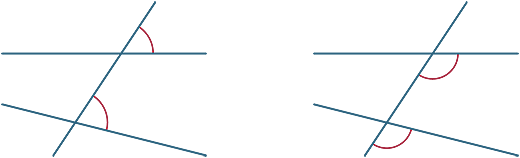
 Wir sehen uns nun an, was passiert, wenn die beiden durch die Transversale geschnittenen Linien parallel sind.
Wir sehen uns nun an, was passiert, wenn die beiden durch die Transversale geschnittenen Linien parallel sind.
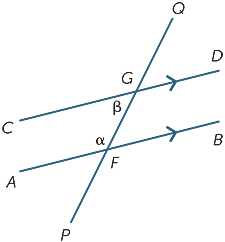
Wenn der Winkel α größer als β wäre, würde CD zunächst AB links von F kreuzen, und wenn er kleiner als β wäre, würde er sich rechts von F kreuzen.
Stellen Sie sich alternativ vor, Sie übersetzen den Winkel QGD entlang GF, bis G mit F übereinstimmt. Da die Linien parallel sind, würden wir erwarten, dass der Winkel α mit dem Winkel β übereinstimmt. Diese Beobachtung führt uns zu der Vermutung, dass:
Entsprechende Winkel, die aus parallelen Linien gebildet werden, sind gleich.
Wir können dieses Ergebnis nicht beweisen, obwohl wir gezeigt haben, dass es geometrisch plausibel ist. Wir werden es als Axiom der Geometrie akzeptieren. Ein Axiom ist eine Aussage, die wir nicht beweisen können, die aber intuitiv vernünftig ist. Beachten Sie, dass viele der bereits genannten Fakten wie: Benachbarte Winkel können hinzugefügt werden, und zwei Punkte bestimmen eine Linie usw., sind auch Axiome, obwohl wir sie nicht explizit auf diese Weise angegeben haben.
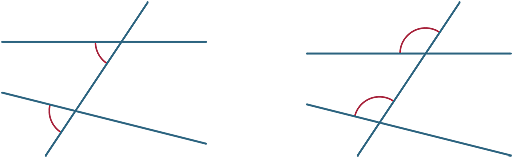
Alternative Winkel
In jedem Diagramm werden die beiden markierten Winkel als alternative Winkel bezeichnet (da sie sich auf alternativen Seiten der Transversalen befinden).

 Wenn die Linien AB und CD parallel sind, sind die alternativen Winkel gleich. Dieses Ergebnis kann nun nachgewiesen werden.
Wenn die Linien AB und CD parallel sind, sind die alternativen Winkel gleich. Dieses Ergebnis kann nun nachgewiesen werden.
![]() DGQ = α (entsprechende Winkel, AB //CD)
DGQ = α (entsprechende Winkel, AB //CD)
![]() DGQ = β (vertikal entgegengesetzte Winkel bei G)
DGQ = β (vertikal entgegengesetzte Winkel bei G)
Also α = β.
Zusammenfassend:
Alternative Winkel, die aus parallelen Linien gebildet werden, sind gleich.
Co-Innenwinkel
Schließlich werden in jedem Diagramm unten die beiden markierten Winkel als Co-Innenwinkel bezeichnet und liegen auf derselben Seite der Transversale.

Wenn die Linien AB und CD parallel sind, ist es offensichtlich, dass die Co-Innenwinkel nicht gleich sind, aber es stellt sich heraus, dass sie komplementär sind, dh ihre Summe beträgt 180 ° .
 Dies ist ein Ergebnis, das auch leicht nachzuweisen ist:
Dies ist ein Ergebnis, das auch leicht nachzuweisen ist:
![]() BFG = β (alternative Winkel, AB ||CD)
BFG = β (alternative Winkel, AB ||CD)
α + β = 180° (gerader Winkel bei F)
Zusammenfassend:
Aus parallelen Linien gebildete Gleichwinkel sind ergänzend.
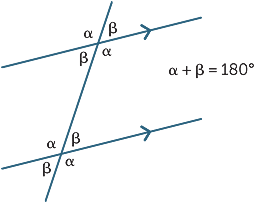 Die drei Ergebnisse lassen sich
Die drei Ergebnisse lassen sich
durch das folgende Diagramm zusammenfassen:
Numerische Beispiele
Angesichts der Informationen über die Winkel in einem Diagramm können wir die obigen Ergebnisse verwenden, um die Größe anderer Winkel im Diagramm zu ermitteln. Dies ist eine einfache, aber sehr wichtige Fähigkeit, die oft informell als Winkeljagd bezeichnet wird. Bei der Lösung von Problemen ist die Abfolge der Schritte nicht immer eindeutig. Es kann verschiedene, aber gleichermaßen gültige Ansätze geben.
Im folgenden Diagramm suchen wir beispielsweise die Größe des Winkels BAC.

![]() DCA = 102° (alternative Winkel, AC/BD)
DCA = 102° (alternative Winkel, AC/BD)
![]() BAC = 78° (Co-Innenwinkel, AB//CD)
BAC = 78° (Co-Innenwinkel, AB//CD)
Übung 4
Verwenden Sie eine alternative Abfolge von Schritten, um ![]() BAC zu finden.
BAC zu finden.
Übung 5
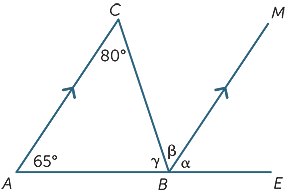 Wenn Sie nur Eigenschaften paralleler Linien verwenden, finden Sie (mit Gründen) die fehlenden Winkel im folgenden Diagramm.
Wenn Sie nur Eigenschaften paralleler Linien verwenden, finden Sie (mit Gründen) die fehlenden Winkel im folgenden Diagramm.
Übung 6
Finden Sie den Wert von α im folgenden Diagramm.
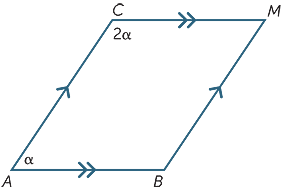
Converse statements
Viele Aussagen in der Mathematik haben eine Umkehrung, in der die Implikation in die entgegengesetzte Richtung geht. Zum Beispiel die Anweisung
‚Jede gerade Zahl endet mit 0, 2, 4, 6 oder 8.‘
has converse
‚Jede Zahl, die mit 0, 2, 4, 6 oder 8 endet, ist gerade.‘
Diese besondere Aussage und ihre Umkehrung sind beide wahr, aber dies ist keineswegs immer
der Fall.
Zum Beispiel sind die folgenden zwei Anweisungen Konversationen voneinander:
‚Jedes Vielfache von 4 ist eine gerade Zahl.‘
‚Jede gerade Zahl ist ein Vielfaches von 4.‘
und hier ist die erste Aussage wahr, aber die zweite ist falsch.
Übung 7
Aufschreiben:
a![]() eine wahre geometrische Aussage, deren Umkehrung ebenfalls wahr ist,
eine wahre geometrische Aussage, deren Umkehrung ebenfalls wahr ist,
b![]() falsche geometrische Aussage, deren Umkehrung wahr ist,
falsche geometrische Aussage, deren Umkehrung wahr ist,
c![]() eine falsche geometrische Aussage, deren Umkehrung ebenfalls falsch ist.
eine falsche geometrische Aussage, deren Umkehrung ebenfalls falsch ist.
Die umgekehrten Sätze für parallele Linien
Wir haben gesehen, dass entsprechende Winkel, die aus parallelen Linien gebildet werden, gleich sind. Wir können die umgekehrte Aussage wie folgt aufschreiben.
Anweisung: Wenn die Linien parallel sind, sind die entsprechenden Winkel gleich.
Converse: Wenn die entsprechenden Winkel gleich sind, sind die Linien parallel.
Die umgekehrte Aussage ist ebenfalls wahr und wird oft verwendet, um zu beweisen, dass zwei Linien parallel sind. Das gleiche gilt in Bezug auf alternative und Co-Innenwinkel.
Anweisung: Wenn die Linien parallel sind, sind die alternativen Winkel gleich.
Umgekehrt: Wenn die alternativen Winkel gleich sind, sind die Linien parallel.
Aussage: Wenn die Linien parallel sind, dann sind die Co-Innenwinkel komplementär.
Converse: Wenn die Co-Innenwinkel komplementär sind, dann sind die Linien parallel.
Somit sind in jedem Diagramm die Linien AB und CD parallel.

Übung 8
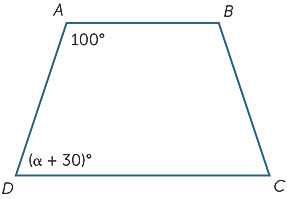 Welcher Wert von α macht AB parallel zu CD?
Welcher Wert von α macht AB parallel zu CD?
Beweise der drei Konversationen
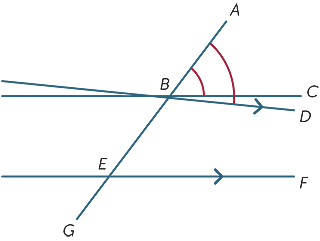 Wir nehmen an, dass die entsprechenden Winkel, die durch die Transversale gebildet werden, gleich sind, und wir zeigen, dass die Linien parallel sind.
Wir nehmen an, dass die entsprechenden Winkel, die durch die Transversale gebildet werden, gleich sind, und wir zeigen, dass die Linien parallel sind.
Im Diagramm nehmen wir an, dass ![]() ABC =
ABC = ![]() BEF.
BEF.
Wenn BC und EF nicht parallel sind, zeichnen Sie
BD parallel zu EF.
Nun, da BD und EF parallel sind ![]() ABD =
ABD = ![]() BEF und so
BEF und so ![]() ABC =
ABC = ![]() ABD, was eindeutig unmöglich ist, es sei denn, die Linien BC und BD sind gleich. Daher sind die Linien BC und EF parallel.
ABD, was eindeutig unmöglich ist, es sei denn, die Linien BC und BD sind gleich. Daher sind die Linien BC und EF parallel.
Die anderen Beweise folgen in gleicher Weise.
Übung 9
Geben Sie einen Beweis für den zweiten umgekehrten Satz (alternative Winkel).
Winkelsumme eines Dreiecks
 Die Ergebnisse aus dem vorherigen Abschnitt können verwendet werden, um eine der wichtigsten Fakten in der Geometrie abzuleiten − die Winkelsumme eines Dreiecks beträgt 180 ° .
Die Ergebnisse aus dem vorherigen Abschnitt können verwendet werden, um eine der wichtigsten Fakten in der Geometrie abzuleiten − die Winkelsumme eines Dreiecks beträgt 180 ° .
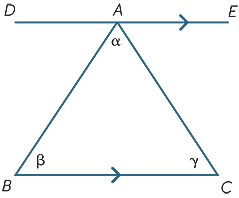
Wir beginnen mit dem Dreieck ABC mit den Winkeln α, β, γ wie gezeigt. Zeichnen Sie die Linie DAE parallel zu BC. Dann,
![]() DAB = β (alternative Winkel, BC//DE)
DAB = β (alternative Winkel, BC//DE)
![]() EAC = γ (alternative Winkel, BC||DE)
EAC = γ (alternative Winkel, BC||DE)
α+ β + γ = 180° (gerader Winkel).
So haben wir den Satz bewiesen
Die Summe der Winkel in einem Dreieck beträgt 180 °.
Ein Viereck ist eine ebene Figur, die von vier Seiten begrenzt wird.
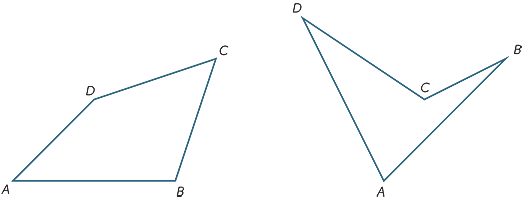
Übung 10
Ermitteln Sie die Summe der Winkel, indem Sie das Viereck ABCD in zwei Dreiecke teilen.
Links forward
Das Material in diesem Modul hat begonnen, die Geometrie auf eine einigermaßen systematische Grundlage sorgfältig definierter Objekte, Axiome, die anzunehmen sind, und Theoreme, die wir bewiesen haben, zu stellen. Auf dieser Grundlage können wir eine systematische Darstellung der Ebenengeometrie entwickeln.:
- Satz des Pythagoras
- Kongruenz und kongruente Dreiecke
- Ähnlichkeit und ähnliche Dreiecke
- gleichschenklige und gleichseitige Dreiecke
- spezielle Vierecke, einschließlich Quadrate, Rechtecke, Parallelogramme, Rauten und Trapeze
- die Geometrie der Kreise.
Die ebene Geometrie wird auch in vielen anderen Bereichen der Mathematik der Jahre 7-10 von grundlegender Bedeutung sein:
- Transformationen
- dreidimensionale Geometrie
- Flächen und Volumen
- Trigonometrie
- Koordinatengeometrie
- die Graphen von Kreisen und Parabeln.
Die Ideen von Tangenten und Flächen führen wiederum in den Jahren 11-12 zur Infinitesimalrechnung.
Geschichte und Anwendung
Geschichte
Die unglaublichen Konstruktionen der Pyramiden und der riesigen Tempel Ägyptens zeigen, dass die Ägypter zumindest auf praktischer Ebene über sehr gute Kenntnisse und ein sehr gutes Verständnis der Grundgeometrie verfügten. Andererseits gibt es keine Hinweise darauf, dass sie dieses Wissen in irgendeiner Form systematisiert haben. Dies wurde den alten Griechen überlassen. Wir haben keine detaillierten Kenntnisse über diese Systematisierung, mit Ausnahme der Behauptung, dass Thales (ca. 624 v. Chr.-ca. 546 v. Chr.) gab die ersten ‚Beweise‘ der geometrischen Tatsachen, die die Anfänge der deduktiven Geometrie markiert. Die pythagoreische Schule setzte diese Arbeit fort und Platon (428 v. Chr. -348 v. Chr.) stützt sich eindeutig auf die Arbeit früherer Mathematiker, wenn er in seinen Schriften geometrische Fakten erwähnt. Der geometrische Dialog in seiner Arbeit the Meno, in dem Sokrates einen Sklavenjungen dazu bringt, durch eine Reihe logischer Schlussfolgerungen zu einem geometrischen Satz zu gelangen, ist lesenswert. Wenn die Ursprünge der Geometrie unklar sind, ist das ‚Endprodukt‘ nicht. Euklid (323-283 v. Chr.), der in Alexandria schrieb, schuf ein bemerkenswertes Werk namens die Elemente, das mehr als 2000 Jahre lang das Standardlehrbuch für Geometrie blieb. In dieser Arbeit legt Euklid eine Reihe von Definitionen (z. B. für Punkte und Linien), Postulaten und allgemeinen Vorstellungen fest. (In diesen Tagen nennen wir sie Axiome.) Aus diesen entwickelte er logisch, in einer sehr sorgfältig gewählten Reihenfolge, sehr viele Theoreme, die wir im Allgemeinen als Euklidische Geometrie. Es gibt eine Reihe anderer geometrischer Ergebnisse, wie den Satz von Pappus, die nach Euklid entdeckt wurden, aber diese werden in der Sekundarschule im Allgemeinen nicht behandelt.
Eines von Euklids fünf Postulaten war nicht so offensichtlich wahr, wie die anderen zu sein schienen. Eine Version davon, bekannt als Playfairs Axiom, besagt, dass: Bei einer Linie  und einem Punkt P, nicht auf
und einem Punkt P, nicht auf  , gibt es eine und nur eine Linie parallel zu
, gibt es eine und nur eine Linie parallel zu  durch P. Im 19.Jahrhundert stellten einige Mathematiker die Frage: Was passiert, wenn wir dieses Postulat ablehnen? Dies geschieht, indem man annimmt, dass es entweder keine solche parallele Linie gibt, oder indem man sagt, dass es mehr als eine solche Linie gibt. Dies führte zur Entwicklung nicht-euklidischer Geometrien, von denen sich eine als eines der guten Modelle für das Universum herausgestellt hat.
durch P. Im 19.Jahrhundert stellten einige Mathematiker die Frage: Was passiert, wenn wir dieses Postulat ablehnen? Dies geschieht, indem man annimmt, dass es entweder keine solche parallele Linie gibt, oder indem man sagt, dass es mehr als eine solche Linie gibt. Dies führte zur Entwicklung nicht-euklidischer Geometrien, von denen sich eine als eines der guten Modelle für das Universum herausgestellt hat.
Anwendungen
In einem sehr realen Sinne bilden Geometrie und geometrische Intuition die Grundlage aller
Mathematik − Geometrie führt zu Koordinatengeometrie, die zu Kalkül und
all ihren vielen Anwendungen führt − und ist daher im Lehrplan von entscheidender Bedeutung.
Auf einer praktischeren Ebene sind Bauherren, Vermesser, Ingenieure und Architekten seit Jahrhunderten starke Anwender von Geometrie und geometrischen Ideen. In jüngerer Zeit, mit der Entwicklung von Computern, haben sich Grafiker und Webdesigner dieser Gruppe von Menschen angeschlossen, die Geometrie in ihrer Arbeit benötigen und verwenden. Auf die Frage, wie nützlich Geometrie ist, Jim Kelly, ein angewandter Wissenschaftler sagte: … geometrie ist ein wichtiger Bestandteil von Design, Zeichnung und Computermodellierung. Es wird auch häufig in verwendet … physik und andere naturwissenschaftliche Kurse als Teil des Verständnisses der Auswirkungen von Lasten auf Strukturen und Ausgleichspunkte (Schwerpunkte) für Verbundkörper. In der Chemie hängt das Verständnis der Geometrie eines Moleküls mit dem Verständnis der Eigenschaften von Substanzen zusammen. Es gibt viele weitere Beispiele. (weitergeleitet von Ask a Scientist).)
Geschichte der Mathematik: Eine Einführung, 3. Auflage, Victor J. Katz, Addison-Wesley, (2008)
Geschichte der Mathematik, D. E. Smith, Dover Publications New York, (1958)
ANTWORTEN AUF ÜBUNGEN
ÜBUNG 1
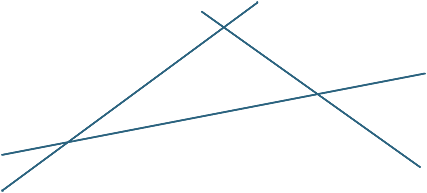
ÜBUNG 2
Die Punkte sind kollinear
ÜBUNG 3
60°
ÜBUNG 4
![]() DBA = 102° (entsprechende Winkel, AB//CD)
DBA = 102° (entsprechende Winkel, AB//CD)
![]() BAC = 78° (Co-Innenwinkel, AC||BD)
BAC = 78° (Co-Innenwinkel, AC||BD)
ÜBUNG 5
α = 65°![]() (entsprechende Winkel, AC||BM)
(entsprechende Winkel, AC||BM)
β = 80°![]() (alternative Winkel, AC||BM)
(alternative Winkel, AC||BM)
γ + β = 115°![]() innenwinkel, AC||BM)
innenwinkel, AC||BM)
Daher γ = 35°
( Dies ist die Struktur für einen Beweis des Ergebnisses, dass die Winkelsumme eines Dreiecks 180 ° beträgt)
ÜBUNG 6
α = 60 °
ÜBUNG 7
a![]() Ein Viereck mit jedem seiner Innenwinkel ein rechter Winkel ist ein Rechteck.
Ein Viereck mit jedem seiner Innenwinkel ein rechter Winkel ist ein Rechteck.
Umgekehrt: Jeder Innenwinkel eines Rechtecks ist ein rechter Winkel.
b![]() Ein Rechteck ist ein Quadrat
Ein Rechteck ist ein Quadrat
Umgekehrt: Ein Quadrat ist ein Rechteck
c![]() Die Winkelsumme der Innenwinkel eines Dreiecks beträgt 200 °
Die Winkelsumme der Innenwinkel eines Dreiecks beträgt 200 °
Umgekehrt: Ein Polygon, für das die Summe des Innenwinkels 200 ° beträgt, ist ein Dreieck.
ÜBUNG 8
α = 50°
ÜBUNG 9
Wir beziehen uns auf dasselbe Diagramm.
Platzieren Sie einen Punkt H auf der Linie EF links von E.
![]() CBE =
CBE = ![]() BEH
BEH
Wenn BC und EF nicht parallel sind, zeichnen Sie BD parallel zu EF.
Da BD und EF parallel sind, ![]() EBD=
EBD= ![]() BEH , was eindeutig unmöglich ist, es sei denn, die Linien BC und BD sind gleich.
BEH , was eindeutig unmöglich ist, es sei denn, die Linien BC und BD sind gleich.
Daher sind die Linien BC und EF parallel.
ÜBUNG 10
360°
Das Projekt Improving Mathematics Education in Schools (TIMES) 2009-2011 wurde vom australischen Ministerium für Bildung, Beschäftigung und Arbeitsbeziehungen finanziert.
Die hier geäußerten Ansichten sind die des Autors und geben nicht unbedingt die Ansichten des australischen Ministeriums für Bildung, Beschäftigung und Arbeitsbeziehungen wieder.
© The University of Melbourne im Auftrag des International Centre of Excellence for Education in Mathematics (ICE-EM), der Bildungsabteilung des Australian Mathematical Sciences Institute (AMSI), 2010 (sofern nicht anders angegeben). Dieses Werk ist lizenziert unter der Creative Commons Namensnennung-Nicht-kommerziell-keine Bearbeitung 3.0 Unported Lizenz.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()