Der Katamorphismus für Entweder ist eine Verallgemeinerung seiner Falte. Der Katamorphismus ermöglicht Operationen, die nicht über Fold verfügbar sind.
Dieser Artikel ist Teil einer Artikelserie über Katamorphismen. Ein Katamorphismus ist eine universelle Abstraktion, die beschreibt, wie eine Datenstruktur in einen potenziell kompakteren Wert umgewandelt wird.
In diesem Artikel wird der Katamorphismus für beide (auch als Ergebnis bezeichnet) sowie seine Identifizierung vorgestellt. Am Anfang dieses Artikels wird der Katamorphismus in C # anhand von Beispielen vorgestellt. Der Rest des Artikels beschreibt, wie der Katamorphismus abgeleitet werden kann. Dieser Teil des Artikels stellt meine Arbeit in Haskell vor. Leser, die mit Haskell nicht vertraut sind, können einfach den ersten Teil lesen und den Rest des Artikels als optionalen Anhang betrachten.
Entweder ist ein Datencontainer, der zwei sich gegenseitig ausschließende Ergebnisse modelliert. Es wird häufig verwendet, um Werte zurückzugeben, die entweder korrekt (rechts) oder falsch (links) sein können. In der statisch typisierten funktionalen Programmierung mit einer Vorliebe für Gesamtfunktionen bietet entweder eine vernünftigere, vernünftigere Möglichkeit, Erfolgs- und Fehlerergebnisse zu modellieren, als Ausnahmen auszulösen.
C# catamorphism #
Dieser Artikel verwendet die Church-Codierung von Beiden. Der Katamorphismus für beide ist die Match -Methode:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
Bis zu diesem Artikel waren alle vorherigen Katamorphismen ein Paar, das aus einem Anfangswert und einer Funktion bestand. Der obige Katamorphismus ist eine Verallgemeinerung, da es sich um ein Funktionspaar handelt. Eine Funktion behandelt den Fall, in dem ein linker Wert vorhanden ist, und die andere Funktion behandelt den Fall, in dem ein rechter Wert vorhanden ist. Beide Funktionen müssen denselben vereinheitlichenden Typ zurückgeben, bei dem es sich häufig um eine Zeichenfolge oder ähnliches handelt, die in einer Benutzeroberfläche angezeigt werden kann:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
Sie werden oft Beispiele wie das obige sehen, die sowohl den linken als auch den rechten Fall in Zeichenfolgen umwandeln oder etwas, das als vereinheitlichender Antworttyp dargestellt werden kann, aber dies ist in keiner Weise erforderlich. Wenn Sie einen vereinheitlichenden Typ finden können, können Sie beide Fälle in diesen Typ konvertieren:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
In den beiden obigen Beispielen verwenden Sie zwei verschiedene Funktionen, die beide die Werte Guid und string auf eine Zahl reduzieren. Die Funktion, die Guid -Werte in eine Zahl umwandelt, zählt, wie viele der Hexadezimalziffern größer oder gleich A (10) sind. Die andere Funktion gibt einfach die Länge von string zurück, falls vorhanden. Dieses Beispiel macht wenig Sinn, aber die Match -Methode kümmert sich nicht darum.
In der Praxis wird Entweder häufig zur Fehlerbehandlung verwendet. Der Artikel über die Kirchenkodierung von Beiden enthält ein Beispiel.
Entweder F-Algebra #
Wie im vorherigen Artikel verwende ich Fix und cata, wie in Bartosz Milewskis ausgezeichnetem Artikel über F-Algebren erläutert.
Während F-Algebren und Fixpunkte hauptsächlich für rekursive Datenstrukturen verwendet werden, können Sie auch eine F-Algebra für eine nicht-rekursive Datenstruktur definieren. Sie haben bereits ein Beispiel dafür in den Artikeln über Booleschen Katamorphismus und vielleicht Katamorphismus gesehen. Der Unterschied zwischen zB Maybe Werten und Entweder ist, dass beide Fälle von Entweder einen Wert tragen. Sie können dies als Functor mit einem Trägertyp und zwei Typargumenten für die Daten modellieren, die entweder enthalten können:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
Ich habe mich entschieden, die ‚Datentypen‘ l (für links) und r (für rechts) und den Trägertyp c (für Träger) aufzurufen. Wie auch bei BoolF und MaybeF ignoriert die Functor -Instanz die Map-Funktion, da der Carrier-Typ sowohl im Fall LeftF als auch im Fall RightF fehlt. Wie bei den Functor -Instanzen für BoolF und MaybeF scheint nichts zu passieren, aber auf Typebene ist dies immer noch eine Übersetzung von EitherF l r c nach EitherF l r c1 . Nicht viel von einer Funktion, vielleicht, aber definitiv ein endofunctor.
Wie es auch bei der Ableitung der Katamorphismen Maybe und List der Fall war, ist Haskell nicht sehr glücklich darüber, Instanzen für einen Typ wie Fix (EitherF l r) zu definieren. Um dieses Problem zu beheben, können Sie einen newtype -Wrapper einführen:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
Sie können definieren Functor, Applicative, Monad, etc. instanzen für diesen Typ, ohne auf funky GHC-Erweiterungen zurückgreifen zu müssen. Denken Sie daran, dass der Zweck all dieses Codes letztendlich nur darin besteht, herauszufinden, wie der Katamorphismus aussieht. Dieser Code ist nicht für den tatsächlichen Gebrauch gedacht.
Ein Paar Hilfsfunktionen erleichtern die Definition von EitherFix -Werten:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
Mit diesen Funktionen können Sie EitherFix Werte erstellen:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
Das ist alles, was Sie brauchen, um den Katamorphismus zu identifizieren.
Haskell catamorphism #
An dieser Stelle haben Sie zwei von drei Elementen einer F-Algebra. Sie haben einen Endofunktor (EitherF l r) und ein Objekt c, aber Sie müssen immer noch einen Morphismus EitherF l r c -> c finden. Beachten Sie, dass die Algebra, die Sie finden müssen, die Funktion ist, die den Funktor auf seinen Trägertyp c reduziert, nicht die ‚Datentypen‘ l und r. Das braucht etwas Zeit, um sich daran zu gewöhnen, aber so funktionieren Katamorphismen. Dies bedeutet jedoch nicht, dass Sie l und r ignorieren können, wie Sie sehen werden.
Beginnen Sie wie in den vorherigen Artikeln mit dem Schreiben einer Funktion, die zum Katamorphismus wird, basierend auf cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
Während dies mit seinen undefined Implementierungen kompiliert wird, macht es offensichtlich nichts Nützliches. Ich finde jedoch, dass es mir hilft zu denken. Wie können Sie einen Wert vom Typ c aus dem Fall LeftF zurückgeben? Sie können ein Argument an die Funktion eitherF übergeben:
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
Während Sie technisch gesehen ein Argument vom Typ c an eitherF übergeben und dann diesen Wert aus dem Fall LeftF zurückgeben könnten, würde dies bedeuten, dass Sie den Wert l ignorieren würden. Dies wäre falsch, also machen Sie das Argument stattdessen zu einer Funktion und rufen Sie es mit l auf. Ebenso können Sie den Fall RightF auf die gleiche Weise behandeln:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
Das funktioniert. Da cata den Typ Functor f => (f a -> a) -> Fix f -> a hat, bedeutet dies, dass alg den Typ f a -> a hat. Im Fall von EitherF schließt der Compiler, dass die Funktion alg den Typ EitherF l r c -> c hat, was genau das ist, was Sie brauchen!
Sie können nun sehen, wofür der Trägertyp c ist. Es ist der Typ, den die Algebra extrahiert, und somit der Typ, den der Katamorphismus zurückgibt.
Dies ist also der Katamorphismus für Beide. Wie bisher konsistent, ist es ein Paar, aber jetzt aus zwei Funktionen. Wie Sie wiederholt gesehen haben, ist dies nicht der einzig mögliche Katamorphismus, da Sie beispielsweise die Argumente trivial auf eitherF umdrehen können.
Ich habe die hier gezeigte Darstellung ausgewählt, weil sie isomorph zur Funktion either aus dem integrierten Modul Data.Either von Haskell ist, das die Funktion „Fallanalyse für den Typ Either“ aufruft. Beide Funktionen (eitherF und either ) entsprechen der obigen C # Match -Methode.
Basis #
Die meisten anderen nützlichen Funktionen können Sie mit eitherF implementieren. Hier ist die Bifunctor -Instanz:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
Aus dieser Instanz folgt die Functor -Instanz trivial:
instance Functor (EitherFix l) where fmap = second
Zusätzlich zu Functor können Sie Applicative hinzufügen:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Beachten Sie, dass die <*> -Implementierung der <*> -Implementierung für MaybeFix ähnelt. Gleiches gilt für die Instanz Monad:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
Nicht nur EitherFix Foldable, es ist Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
Beachten Sie interessanterweise, dass bifoldMap identisch mit eitherF ist.
Mit der Bifoldable -Instanz können Sie die Foldable -Instanz trivial implementieren:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
Sie können das Vorhandensein von mempty rätselhaft finden, da bifoldMap (oder eitherF; sie sind identisch) als Argumente zwei Funktionen verwendet. Ist mempty eine Funktion?
Ja, mempty kann eine Funktion sein. Hier ist es. Es gibt eine Monoid -Instanz für jede Funktion a -> m, wobei m eine Monoid -Instanz ist und mempty die Identität für dieses Monoid ist. Das ist die hier verwendete Instanz.
So wie EitherFix Bifoldable ist, ist es auch Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
Sie können die Traversable -Instanz basierend auf der Bitraversable -Instanz bequem implementieren:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
Schließlich können Sie Konvertierungen in und aus dem Standardtyp Either implementieren, wobei ana als cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
Dies zeigt, dass EitherFix isomorph zu Either ist, was wiederum feststellt, dass eitherF und either äquivalent sind.
Beziehungen #
In dieser Serie haben Sie verschiedene Beispiele für Katamorphismen von Strukturen gesehen, die keine Falten haben, Katamorphismen, die mit Falten übereinstimmen, und jetzt einen Katamorphismus, der allgemeiner ist als die Falte. Die Einführung in die Serie enthielt dieses Diagramm:
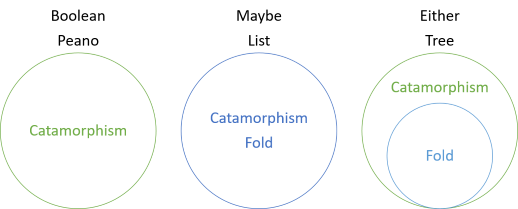
Dies zeigt, dass Boolesche Werte und Peano-Zahlen Katamorphismen haben, aber keine Falten, während für Maybe und List die Falte und der Katamorphismus gleich sind. Für beide ist die Falte jedoch ein Sonderfall des Katamorphismus. Die Falte für Beide ‚gibt vor‘, dass die linke Seite nicht existiert. Stattdessen wird der linke Wert als fehlender rechter Wert interpretiert. Um beide Werte zu falten, müssen Sie daher einen Fallback-Wert angeben, der verwendet wird, falls ein beider Werte kein richtiger Wert ist:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
In einer GHCi-Sitzung wie der obigen können Sie zwei separate Werte desselben Typs erstellen. Der rechte Fall ist ein Ordering -Wert, während der linke Fall ein Integer -Wert ist.
Mit foldr gibt es keine Möglichkeit, auf den linken Fall zuzugreifen. Während Sie auf den rechten Ordering -Wert zugreifen und ihn transformieren können, wird die Zahl 42 während des Faltens einfach ignoriert. Stattdessen wird der Standardwert "" zurückgegeben.
Vergleichen Sie dies mit dem Katamorphismus, der auf beide Fälle zugreifen kann:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
In einer Sitzung wie dieser erstellen Sie dieselben Werte neu, aber mit dem Katamorphismus eitherF können Sie jetzt auf den linken und den rechten Fall zugreifen und ihn transformieren. Mit anderen Worten, der Katamorphismus ermöglicht es Ihnen, Operationen auszuführen, die mit der Falte nicht möglich sind.
Es ist jedoch interessant festzustellen, dass die Falte zwar eine Spezialisierung des Katamorphismus ist, die Bifold jedoch mit dem Katamorphismus identisch ist.
Zusammenfassung #
Der Katamorphismus für Beide ist ein Paar von Funktionen. Eine Funktion transformiert den linken Fall, während die andere Funktion den rechten Fall transformiert. Für jeden beliebigen Wert wird nur eine dieser Funktionen verwendet.
Als ich ursprünglich auf das Konzept eines Katamorphismus stieß, fiel es mir schwer, zwischen Katamorphismus und Falte zu unterscheiden. Mein Problem war, glaube ich, dass die Tutorials, auf die ich gestoßen bin, hauptsächlich verknüpfte Listen verwendeten, um zu demonstrieren, wie in diesem Fall die Falte der Katamorphismus ist. Es stellt sich jedoch heraus, dass dies nicht immer der Fall ist. Ein Katamorphismus ist eine allgemeine Abstraktion. Eine Falte hingegen scheint mir hauptsächlich mit Sammlungen zu tun zu haben.
In diesem Artikel haben Sie das erste Beispiel eines Katamorphismus gesehen, der mehr kann als die Falte. Für beide ist die Falte nur ein Sonderfall des Katamorphismus. Sie haben jedoch auch gesehen, wie der Katamorphismus mit dem Bifold identisch war. Daher ist immer noch nicht ganz klar, wie diese Konzepte zusammenhängen. Daher erhalten Sie im nächsten Artikel ein Beispiel für einen Container, in dem es keine Bifold gibt und in dem der Katamorphismus tatsächlich eine Verallgemeinerung der Falte ist.
Weiter: Baumkatamorphismus.