Heute wird eine kurze Einführung in die zirkuläre Statistik (manchmal auch als Richtungsstatistik bezeichnet) gegeben. Die zirkuläre Statistik ist eine interessante Unterteilung von Statistiken, die Beobachtungen als Vektoren um einen Einheitskreis umfassen. Stellen Sie sich als Beispiel vor, Sie messen die Geburtszeiten in einem Krankenhaus über einen 24-Stunden-Zyklus oder die gerichtete Streuung einer Gruppe wandernder Tiere. Diese Art von Daten ist in einer Vielzahl von Bereichen wie Ökologie, Klimatologie und Biochemie beteiligt. Die Art der Messung von Beobachtungen um einen Einheitskreis erfordert einen anderen Ansatz für Hypothesentests. Verteilungen müssen um den Kreis „gewickelt“ werden, um von Nutzen zu sein, und herkömmliche Schätzer wie der Stichprobenmittelwert oder die Stichprobenvarianz halten kein Wasser.
In diesem Beitrag werden wir den Rao-Abstandstest durchführen, um die Einheitlichkeit eines kreisförmigen Datensatzes zu bewerten. Dies ist ein grundlegendes Verfahren und sollte als Einführung in den Umgang mit zirkulären Daten betrachtet werden.
Erste Schritte
Wir werden einen Hypothesentest an Schildkröten durchführen, einen kleinen Datensatz, der aus den Ankunftswinkeln von 10 grünen Meeresschildkröten zu ihrer Nistinsel besteht. Unser Ziel ist es zu bestimmen, wo die Ankunftswinkel Anzeichen von Direktionalität zeigen oder eher auf eine zufällige Streuung hindeuten.
Installieren Sie zuerst das Paket circular und hängen Sie das Turtles-Dataset an.
install.packages("circular")require(circular)attach(turtles)
Plotten der Daten
Das Paket circular enthält eine eigene Plotfunktion, plot.circular. Beobachten wir die Ankunftswinkel der Schildkröten.
plot.circular(arrival)
Hier ist die Handlung: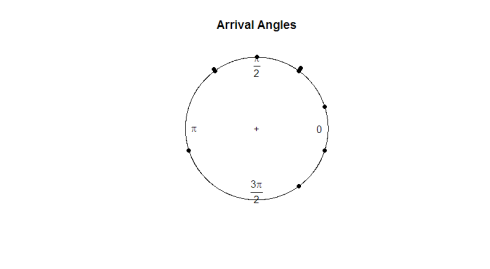
Angesichts des Sehtests scheinen die Beobachtungen im Kreis einheitlich zu sein. Wenn wir einen Hypothesentest durchführen möchten, um festzustellen, ob die Daten wirklich einheitlich sind, müssen wir eine Teststatistik entwickeln, die mit eckigen Daten funktioniert.
Was ist ein guter Parameter für uns? Der Mittelwert der Stichprobe sagt nicht viel über die Richtung der Daten aus (180 Grad sind kein nützlicher Mittelwert von 2 Grad und 358 Grad). Beobachten Sie im folgenden Diagramm, wie der Stichprobenmittelwert für die Darstellung der Form oder Ausbreitung unserer Daten von keinem Nutzen ist.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
Hier ist die Handlung: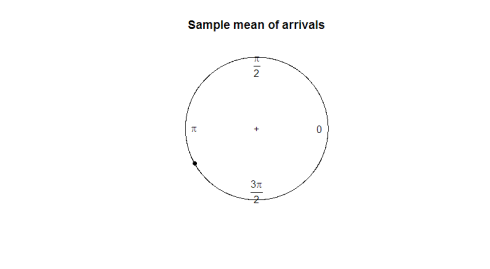
Stattdessen verwenden wir eine Methode, die die Direktionalität bestimmt, indem der durchschnittliche Abstand zwischen den Beobachtungen gemessen wird. Dieser Test wird als Rao-Abstandstest bezeichnet.
Raos Abstandstest
Der Rao-Abstandstest wurde entwickelt, um die Einheitlichkeit kreisförmiger Daten zu bewerten. Es verwendet den Abstand zwischen den Beobachtungen, um festzustellen, ob die Daten eine signifikante Direktionalität aufweisen. Wenn die Daten einheitlich sind, sollten die Beobachtungen in der Regel gleichmäßig voneinander beabstandet sein.
Hier ist die Teststatistik \(U\) für Raos Abstandstest: $$U = 1/2\sum\limits_{i=1}^n |T_{i} – λ/ $$ wobei \(λ = 360/n, T_{i} = f_{i+1}-f_{i}\) und \(T_{n} = (360-f_{n})+f_{1}\)
Grundsätzlich aggregiert die Teststatistik die Abweichungen zwischen aufeinanderfolgenden Punkten, die jeweils mit der Gesamtzahl der Beobachtungen im Datensatz gewichtet werden.
Wir werden die Funktion rao.spacing.test() verwenden, um diesen Hypothesentest auszuführen. Unsere Nullhypothese besagt, dass die Daten gleichmäßig verteilt sind, während die Alternative besagt, dass die Daten Anzeichen von Direktionalität aufweisen. Lass uns den Test machen.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
Mit einer Teststatistik von 127, die unter den kritischen Wert von 161 fällt, lehnen sich die Daten nicht signifikant in irgendeine Richtung. Wir können die Hypothese nicht ablehnen, dass die ankommenden Schildkröten gleichmäßig verteilt sind.
Fazit
Der Rao-Abstandstest ergab, dass die Daten keine Anzeichen von Richtungstrends zeigten. Wir können die Nullhypothese der Uniformität nicht ablehnen und werden Uniformität in Bezug auf die Ankunftsrichtung annehmen. Während dieser Beitrag ein relativ einfaches Tutorial war, haben viele Leute in der Data Science Community noch nicht mit zirkulären Daten gearbeitet. Es ist ein interessantes Unterthema, in das man eintauchen kann, sowie ein junges Feld der Statistik, das sich noch entwickelt.
Schlussbemerkungen
Ich möchte S. Rao Jammalamadaka PhD von der University of California, Santa Barbara, und seinem Lehrbuch „Topics in Circular Statistics“ dafür danken, dass sie mein Interesse am Bereich der Circular Statistics geweckt haben.