4.2 Schätzung der Koeffizienten des linearen Regressionsmodells / Einführung in die Ökonometrie mit R

4.2 Schätzung der Koeffizienten des linearen Regressionsmodells

In der Praxis sind der Achsenabschnitt \ (\beta_0\) und die Steigung $\beta_1$ der Populationsregressionsgeraden unbekannt. Daher müssen wir Daten verwenden, um beide unbekannten Parameter abzuschätzen. Im Folgenden wird anhand eines realen Beispiels gezeigt, wie dies erreicht wird. Wir möchten die Testergebnisse mit den in kalifornischen Schulen gemessenen Schüler-Lehrer-Verhältnissen in Beziehung setzen. Das Testergebnis ist der bezirksweite Durchschnitt der Lese- und Mathematikwerte für Fünftklässler. Auch hier wird die Klassengröße als die Anzahl der Schüler geteilt durch die Anzahl der Lehrer (das Schüler-Lehrer-Verhältnis) gemessen. Was die Daten betrifft, so enthält der California School Data Set (CASchools) ein R-Paket namens AER, ein Akronym für Angewandte Ökonometrie mit R (Kleiber und Zeileis 2020). Nach der Installation des Pakets mit install.pakete („AER“) und Anhängen mit Bibliothek(AER) Der Datensatz kann mit der Funktion data() geladen werden.

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

Sobald ein Paket installiert wurde, kann es bei weiteren Gelegenheiten verwendet werden, wenn es mit library() aufgerufen wird — es ist nicht erforderlich, install auszuführen.pakete() wieder!

Es ist interessant zu wissen, mit welcher Art von Objekt wir es zu tun haben.class() gibt die Klasse eines Objekts zurück. Abhängig von der Klasse eines Objekts verhalten sich einige Funktionen (z. B. plot() und summary()) unterschiedlich.

Überprüfen wir die Klasse des Objekts CASchools.

class(CASchools)#> "data.frame"

Es stellt sich heraus, dass CASchools von Klassendaten ist.frame, mit dem Sie bequem arbeiten können, insbesondere zur Durchführung von Regressionsanalysen.

Mit Hilfe von head() erhalten wir einen ersten Überblick über unsere Daten. Diese Funktion zeigt nur die ersten 6 Zeilen des Datensatzes an, was eine überfüllte Konsolenausgabe verhindert.

Drücken Sie Strg + L, um die Konsole zu löschen. Dieser Befehl löscht jeglichen Code, der von Ihnen eingegeben und ausgeführt oder von R functions auf die Konsole gedruckt wurde. Die gute Nachricht: Alles andere bleibt unberührt. Sie verlieren weder definierte Variablen usw. noch die Code-Geschichte. Es ist weiterhin möglich, zuvor ausgeführte R-Befehle mit den Aufwärts- und Abwärtstasten abzurufen. Wenn Sie in RStudio arbeiten, drücken Sie Strg + Auf Ihrer Tastatur (CMD + Auf einem Mac), um eine Liste der zuvor eingegebenen Befehle anzuzeigen.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

Wir finden, dass der Datensatz aus vielen Variablen besteht und dass die meisten von ihnen numerisch sind.

Übrigens: Eine Alternative zu class() und head() ist str(), das aus ’structure‘ abgeleitet wird und einen umfassenden Überblick über das Objekt gibt. Versuch’s mal!

Zurück zu CASchools, die beiden Variablen, an denen wir interessiert sind (dh., durchschnittliche Testergebnisse und das Schüler-Lehrer-Verhältnis) sind nicht enthalten. Es ist jedoch möglich, beide aus den bereitgestellten Daten zu berechnen. Um die Schüler-Lehrer-Verhältnisse zu erhalten, teilen wir einfach die Anzahl der Schüler durch die Anzahl der Lehrer. Die durchschnittliche Testpunktzahl ist das arithmetische Mittel der Testpunktzahl zum Lesen und der Punktzahl des Mathe-Tests. Der nächste Codeblock zeigt, wie die beiden Variablen als Vektoren konstruiert und an CASchools angehängt werden können.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

Wenn wir head(CASchools) erneut ausführen würden, würden wir die beiden Variablen von Interesse als zusätzliche Spalten mit den Namen STR und score (überprüfen Sie dies!).

Tabelle 4.1 aus dem Lehrbuch fasst die Verteilung der Testergebnisse und des Schüler-Lehrer-Verhältnisses zusammen. Es gibt verschiedene Funktionen, die verwendet werden können, um ähnliche Ergebnisse zu erzielen, z.,

mean() (berechnet das arithmetische Mittel der angegebenen Zahlen),
sd() (berechnet die Standardabweichung der Stichprobe),
quantile() (gibt einen Vektor der angegebenen Abtastquantile für die Daten zurück).

Der nächste Codeblock zeigt, wie dies erreicht werden kann. Zuerst berechnen wir zusammenfassende Statistiken über die Spalten STR und Score von CASchools. Um eine schöne Ausgabe zu erhalten, sammeln wir die Maßnahmen in Daten.frame mit dem Namen DistributionSummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

Für die Beispieldaten verwenden wir plot() . Auf diese Weise können wir Merkmale unserer Daten erkennen, z. B. Ausreißer, die durch bloße Zahlen schwerer zu entdecken sind. Dieses Mal fügen wir dem Aufruf von plot() einige zusätzliche Argumente hinzu.

Das erste Argument in unserem Aufruf von plot(), score ~ STR , ist wiederum eine Formel, die Variablen auf der y- und der x-Achse angibt. Diesmal werden die beiden Variablen jedoch nicht in separaten Vektoren gespeichert, sondern sind Spalten von CASchools. Daher würde R sie nicht finden, ohne dass die Argumentdaten korrekt angegeben wären. die Daten müssen mit dem Namen der Daten übereinstimmen.frame, zu dem die Variablen gehören, in diesem Fall CASchools. Weitere Argumente werden verwendet, um das Erscheinungsbild des Diagramms zu ändern: Während main einen Titel hinzufügt, fügen xlab und ylab benutzerdefinierte Beschriftungen für beide Achsen hinzu.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")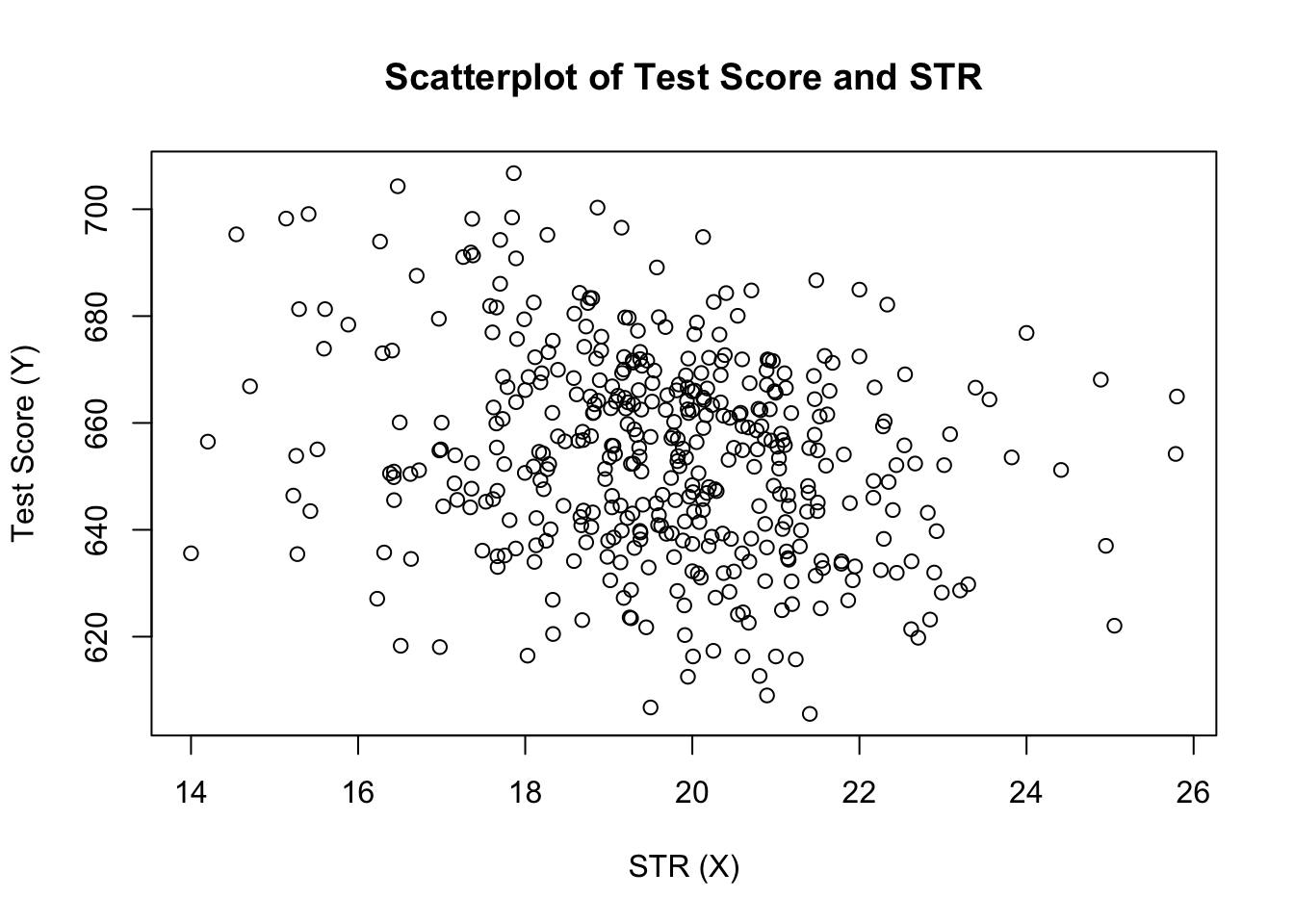

Das Diagramm (Abbildung 4.2 im Buch) zeigt das Streudiagramm aller Beobachtungen zum Schüler-Lehrer-Verhältnis und zur Testpunktzahl. Wir sehen, dass die Punkte stark verstreut sind und dass die Variablen negativ korreliert sind. Das heißt, wir erwarten niedrigere Testergebnisse in größeren Klassen.

Die Funktion cor() (siehe ?cor für weitere Informationen) kann verwendet werden, um die Korrelation zwischen zwei numerischen Vektoren zu berechnen.

cor(CASchools$STR, CASchools$score)#> -0.2263627

Wie das Streudiagramm bereits vermuten lässt, ist die Korrelation negativ, aber eher schwach.

Die Aufgabe, vor der wir jetzt stehen, besteht darin, eine Zeile zu finden, die am besten zu den Daten passt. Natürlich könnten wir einfach bei der grafischen Inspektion und Korrelationsanalyse bleiben und dann die am besten passende Linie durch Augapfel auswählen. Dies wäre jedoch eher subjektiv: Verschiedene Beobachter würden unterschiedliche Regressionslinien zeichnen. Aus diesem Grund interessieren wir uns für Techniken, die weniger willkürlich sind. Eine solche Technik wird durch gewöhnliche Schätzung der kleinsten Quadrate (OLS) gegeben.

Der gewöhnliche Schätzer der kleinsten Quadrate

Der OLS-Schätzer wählt die Regressionskoeffizienten so aus, dass die geschätzte Regressionslinie so „nah“ wie möglich an den beobachteten Datenpunkten liegt. Hier wird die Nähe durch die Summe der quadratischen Fehler gemessen, die bei der Vorhersage von \ (Y\) bei \ (X \) gemacht wurden. Seien $b_0$ und $b_1$ einige Schätzer von $\beta_0$ und $\beta_1$. Dann kann die Summe der quadratischen Schätzfehler ausgedrückt werden als

Der OLS-Schätzer im einfachen Regressionsmodell ist das Schätzerpaar für Achsenabschnitt und Steigung, das den obigen Ausdruck minimiert. Die Ableitung der OLS-Schätzer für beide Parameter ist in Anhang 4.1 des Buches dargestellt. Die Ergebnisse sind im Schlüsselkonzept 4.2 zusammengefasst.

Der OLS-Schätzer, vorhergesagte Werte und Residuen

Die OLS-Schätzer der Steigung $\beta_1$ und des Abschnitts $\beta_0$ im einfachen linearen Regressionsmodell sind\Die OLS-Vorhersagewerte $\widehat{Y}_i$ und Residuen $\hat{u}_i$ sind\

Der geschätzte Abschnitt $\hat {\beta}_0$, der Slope-Parameter $\hat{\beta}_1$ und die Residuen $\left(\hat{u}_i\right)$ werden aus einer Stichprobe von $n$ Beobachtungen von $X_i$ und $Y_i$, $i$, $ berechnet…$, $und$. Dies sind Schätzungen des unbekannten Populationsabschnitts $\left(\beta_0 \right)$, der Steigung $\left (\beta_1\right)$ und des Fehlerterms $(u_i) $.

Die oben dargestellten Formeln sind auf den ersten Blick möglicherweise nicht sehr intuitiv. Die folgende interaktive Anwendung soll Ihnen helfen, die Mechanik von OLS zu verstehen. Sie können Beobachtungen hinzufügen, indem Sie in das Koordinatensystem klicken, in dem die Daten durch Punkte dargestellt werden. Sobald zwei oder mehr Beobachtungen verfügbar sind, berechnet die Anwendung eine Regressionsgerade mit OLS und einigen Statistiken, die im rechten Bereich angezeigt werden. Die Ergebnisse werden aktualisiert, wenn Sie dem linken Bereich weitere Beobachtungen hinzufügen. Ein Doppelklick setzt die Anwendung zurück, d. H. Alle Daten werden entfernt.

Es gibt viele Möglichkeiten, $\hat{\beta}_0$ und $\hat{\beta}_1$ in R zu berechnen. Zum Beispiel könnten wir die Formeln in Key Concept 4.2 mit zwei der grundlegendsten Funktionen von R implementieren: mean() und sum(). Zuvor fügen wir den CASchools-Datensatz hinzu.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

Wenn wir attach(CASchools) aufrufen, können wir eine in CASchools enthaltene Variable anhand ihres Namens ansprechen: es ist nicht mehr notwendig, den Operator $ in Verbindung mit der Datenmenge zu verwenden: R kann den Variablennamen direkt auswerten.

R verwendet das Objekt in der Benutzerumgebung, wenn dieses Objekt den Namen der in einer angehängten Datenbank enthaltenen Variablen teilt. Es ist jedoch eine bessere Praxis, immer unverwechselbare Namen zu verwenden, um solche (scheinbar) Ambivalenzen zu vermeiden!

Beachten Sie, dass wir Variablen, die im angehängten Datensatz CASchools enthalten sind, für den Rest dieses Kapitels direkt ansprechen!

Natürlich gibt es noch mehr manuelle Möglichkeiten, diese Aufgaben auszuführen. Da OLS eine der am weitesten verbreiteten Schätztechniken ist, enthält R natürlich bereits eine integrierte Funktion namens lm() (lineares Modell), mit der eine Regressionsanalyse durchgeführt werden kann.

Das erste Argument der zu spezifizierenden Funktion ist, ähnlich wie plot(), die Regressionsformel mit der grundlegenden Syntax y ~ x, wobei y die abhängige Variable und x die erklärende Variable ist. Das Argument data bestimmt den Datensatz, der in der Regression verwendet werden soll. Wir betrachten nun das Beispiel aus dem Buch, in dem die Beziehung zwischen den Testergebnissen und den Klassengrößen analysiert wird. Der folgende Code verwendet lm(), um die in Abbildung 4.3 des Buches dargestellten Ergebnisse zu replizieren.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

Fügen wir die geschätzte Regressionslinie zum Diagramm hinzu. Dieses Mal vergrößern wir auch die Bereiche beider Achsen, indem wir die Argumente xlim und ylim setzen.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)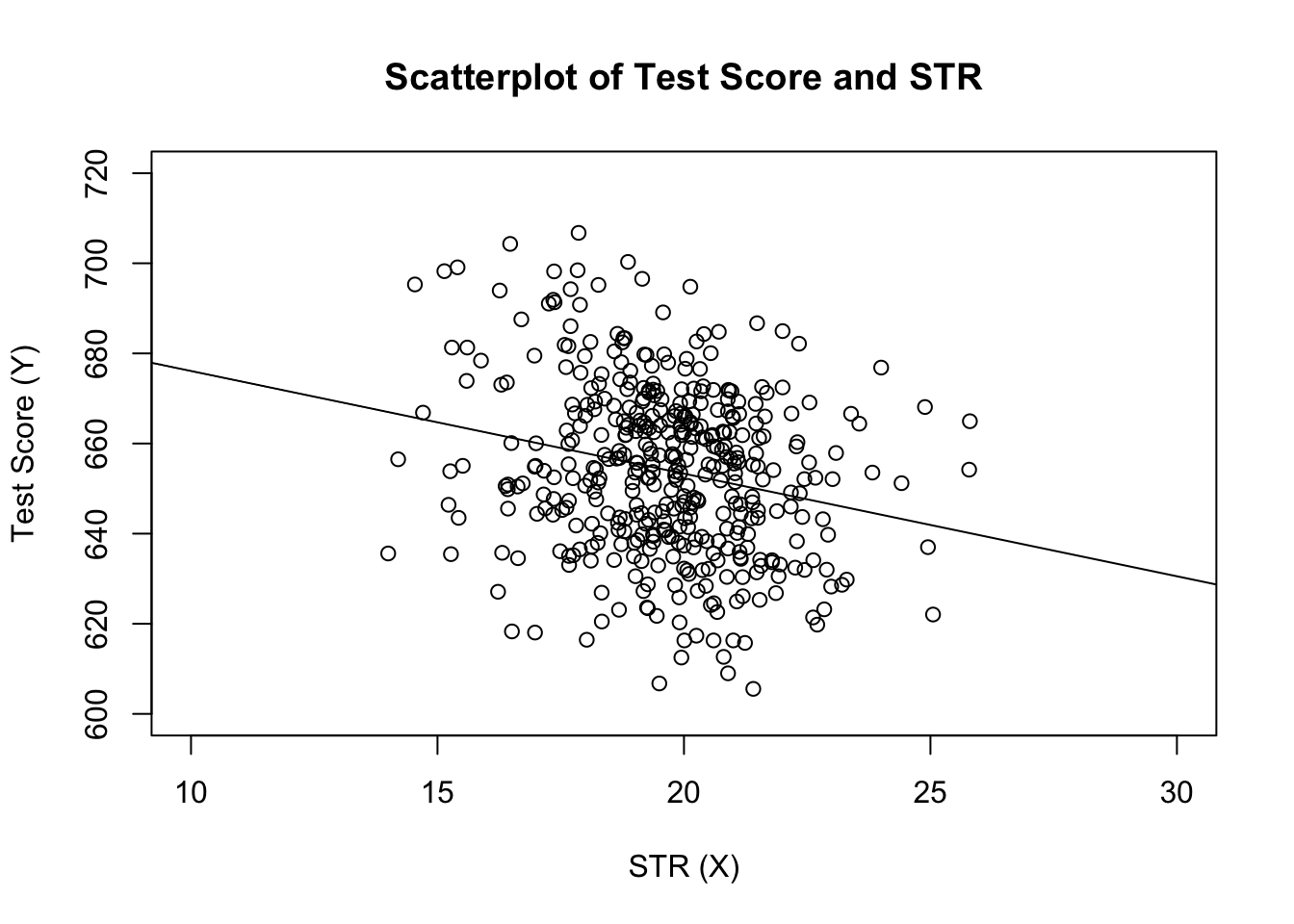

Haben Sie bemerkt, dass wir diesmal die Parameter intercept und slope nicht an abline übergeben haben? Wenn Sie abline() für ein Objekt der Klasse lm aufrufen, das nur einen einzigen Regressor enthält, zeichnet R die Regressionslinie automatisch!