Bewertung | Biopsychologie | Vergleichende | Kognitive | Entwicklungs | Sprache | Individuelle Unterschiede |Persönlichkeit | Philosophie | Soziales |
Methoden | Statistik |Klinische | Pädagogische | Industrielle | Professionelle Artikel | Weltpsychologie |
Statistik:Wissenschaftliche Methode · Forschungsmethoden · Experimentelles Design · Statistikkurse für Studenten · Statistische Tests · Spieltheorie · Entscheidungstheorie
Bitte helfen Sie, diese Seite selbst zu verbessern, wenn Sie können..
Clusteranalyse oder Clustering ist eine gängige Technik zur statistischen Datenanalyse, die in vielen Bereichen eingesetzt wird, darunter maschinelles Lernen, Data Mining, Mustererkennung, Bildanalyse und Bioinformatik. Clustering ist die Klassifizierung ähnlicher Objekte in verschiedene Gruppen oder genauer gesagt die Partitionierung eines Datensatzes in Teilmengen (Cluster), so dass die Daten in jeder Teilmenge (idealerweise) ein gemeinsames Merkmal aufweisen – oft die Nähe nach einem definierten Entfernungsmaß.
Neben dem Begriff Datenclustering (oder nur Clustering) gibt es eine Reihe von Begriffen mit ähnlichen Bedeutungen, darunter Clusteranalyse, automatische Klassifizierung, numerische Taxonomie, Botryologie und typologische Analyse.
- Clustertypen
- Hierarchisches Clustering
- Entfernungsmaß
- Erstellen von Clustern
- Agglomeratives hierarchisches Clustering
- Partitional Clustering
- k-Means und Derivate
- K-means Clustering
- QT Clust algorithm
- Fuzzy c-bedeutet Clustering
- Ellenbogenkriterium
- Spectral clustering
- Anwendungen
- Biologie
- Marktforschung
- Andere Anwendungen
- Vergleiche zwischen Datenclustern
- Siehe auch
- Bibliographie
- Softwareimplementierungen
- Kostenlos
Clustertypen
Datenclusteralgorithmen können hierarchisch oder partitionell sein. Hierarchische Algorithmen finden aufeinanderfolgende Cluster unter Verwendung zuvor etablierter Cluster, während partitionelle Algorithmen alle Cluster gleichzeitig bestimmen. Hierarchische Algorithmen können agglomerativ (Bottom-up) oder divisiv (Top-down) sein. Agglomerative Algorithmen beginnen mit jedem Element als separatem Cluster und führen sie in sukzessive größeren Clustern zusammen. Teilungsalgorithmen beginnen mit dem gesamten Satz und teilen ihn in sukzessive kleinere Cluster auf.
Hierarchisches Clustering
Entfernungsmaß
Ein wichtiger Schritt in einem hierarchischen Clustering ist die Auswahl eines Entfernungsmaßes. Ein einfaches Maß ist die Manhattan-Entfernung, gleich der Summe der absoluten Entfernungen für jede Variable. Der Name kommt von der Tatsache, dass in einem Fall mit zwei Variablen die Variablen in einem Raster dargestellt werden können, das mit Stadtstraßen verglichen werden kann, und der Abstand zwischen zwei Punkten die Anzahl der Blöcke ist, die eine Person gehen würde.
Ein häufigeres Maß ist die euklidische Entfernung, die berechnet wird, indem das Quadrat der Entfernung zwischen den einzelnen Variablen ermittelt, die Quadrate summiert und die Quadratwurzel dieser Summe ermittelt wird. Im Fall von zwei Variablen ist der Abstand analog zum Ermitteln der Länge der Hypotenuse in einem Dreieck; das heißt, es ist der Abstand „in Luftlinie.“ Eine Überprüfung der Clusteranalyse in der gesundheitspsychologischen Forschung ergab, dass das häufigste Entfernungsmaß in veröffentlichten Studien in diesem Forschungsbereich die euklidische Entfernung oder die quadratische euklidische Entfernung ist.
Erstellen von Clustern
Bei einem Distanzmaß können Elemente kombiniert werden. Hierarchisches Clustering baut (agglomerativ) oder bricht (divisiv) eine Hierarchie von Clustern auf. Die traditionelle Darstellung dieser Hierarchie ist eine Baumdatenstruktur (Dendrogramm genannt) mit einzelnen Elementen an einem Ende und einem einzelnen Cluster mit jedem Element am anderen Ende. Agglomerative Algorithmen beginnen oben im Baum, während divisive Algorithmen unten beginnen. (In der Abbildung zeigen die Pfeile ein agglomeratives Clustering an.)
Wenn Sie den Baum in einer bestimmten Höhe schneiden, erhalten Sie ein Clustering mit einer ausgewählten Genauigkeit. Im folgenden Beispiel ergibt das Schneiden nach der zweiten Reihe Cluster {a} {b c} {d e} {f}. Das Schneiden nach der dritten Reihe ergibt Cluster {a} {b c} {d e f}, was ein gröberes Clustering mit einer geringeren Anzahl größerer Cluster ist.
Agglomeratives hierarchisches Clustering
Angenommen, diese Daten sollen gruppiert werden. Wobei die euklidische Entfernung die Entfernungsmetrik ist.
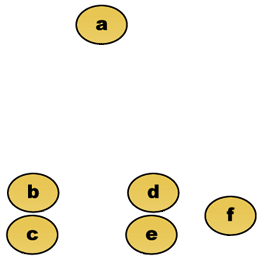
Rohdaten
Das hierarchische Clustering-Dendrogramm wäre als solches:
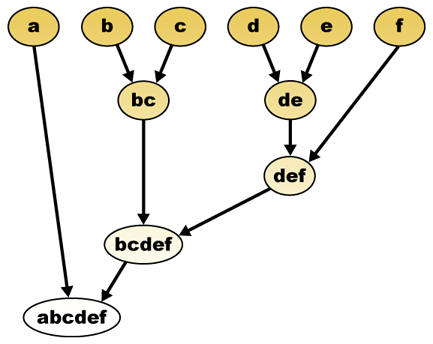
Traditionelle Vertretung
Diese Methode baut die Hierarchie aus den einzelnen Elementen auf, indem Cluster schrittweise zusammengeführt werden. Auch hier haben wir sechs Elemente {a} {b} {c} {d} {e} und {f}. Der erste Schritt besteht darin, zu bestimmen, welche Elemente in einem Cluster zusammengeführt werden sollen. Normalerweise wollen wir die beiden nächstgelegenen Elemente nehmen, deshalb müssen wir einen Abstand definieren 
Angenommen, wir haben die beiden nächstgelegenen Elemente b und c zusammengeführt, wir haben jetzt die folgenden Cluster {a}, {b, c}, {d}, {e} und {f} und möchten sie weiter zusammenführen. Aber dazu müssen wir den Abstand zwischen {a} und {bc} nehmen und daher den Abstand zwischen zwei Clustern definieren. Normalerweise ist der Abstand zwischen zwei Clustern 
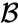
- Der maximale Abstand zwischen Elementen jedes Clusters (auch als vollständiges Linkage-Clustering bezeichnet):
- Der Mindestabstand zwischen Elementen jedes Clusters (auch Single Linkage Clustering genannt):
- Der mittlere Abstand zwischen den Elementen jedes Clusters (auch als durchschnittliches Verknüpfungsclustering bezeichnet):
- Die Summe aller Intra-Cluster-Varianzen
- Die Zunahme der Varianz für den Cluster, der zusammengeführt wird (Ward-Kriterium)
- Die Wahrscheinlichkeit, dass Kandidatencluster aus derselben Verteilungsfunktion hervorgehen (V-Verknüpfung)
Jede Agglomeration tritt in einem größeren Abstand zwischen Clustern auf als die vorherige Agglomeration, und man kann entscheiden, die Clusterbildung entweder zu beenden, wenn die Cluster zu weit voneinander entfernt sind, um zusammengeführt zu werden (Entfernungskriterium) oder wenn eine ausreichend kleine Anzahl von Clustern vorhanden ist (Zahlenkriterium).
Partitional Clustering
k-Means und Derivate
K-means Clustering
Der K-means-Algorithmus weist jeden Punkt dem Cluster zu, dessen Zentrum (auch Centroid genannt) am nächsten liegt. Das Zentrum ist der Durchschnitt aller Punkte im Cluster — das heißt, seine Koordinaten sind das arithmetische Mittel für jede Dimension separat über alle Punkte im Cluster.
Beispiel: Der Datensatz hat drei Dimensionen und der Cluster hat zwei Punkte: X = (x1, x2, x3) und Y = (y1, y2, y3). Dann wird der Schwerpunkt Z zu Z = (z1, z2, z3), wobei z1 = (x1 + y1)/2 und z2 = (x2 + y2)/2 und z3 = (x3 + y3)/2.
Der Algorithmus ist grob (J. MacQueen, 1967):
- Generieren Sie zufällig k Cluster und bestimmen Sie die Clusterzentren oder generieren Sie direkt k Startpunkte als Clusterzentren.
- Weisen Sie jeden Punkt dem nächstgelegenen Clusterzentrum zu.
- Berechnen Sie die neuen Clusterzentren neu.
- Wiederholen, bis ein Konvergenzkriterium erfüllt ist (normalerweise, dass sich die Zuordnung nicht geändert hat).
Die Hauptvorteile dieses Algorithmus sind seine Einfachheit und Geschwindigkeit, die es ermöglicht, auf großen Datensätzen zu laufen. Sein Nachteil ist, dass es nicht bei jedem Lauf das gleiche Ergebnis liefert, da die resultierenden Cluster von den anfänglichen zufälligen Zuweisungen abhängen. Es maximiert die Varianz zwischen Clustern (oder minimiert die Varianz innerhalb von Clustern), stellt jedoch nicht sicher, dass das Ergebnis ein globales Minimum an Varianz aufweist.
QT Clust algorithm
QT (Quality Threshold) Clustering (Heyer et al, 1999) ist eine alternative Methode zur Partitionierung von Daten, die für das Genclustering erfunden wurde. Es erfordert mehr Rechenleistung als k-means, erfordert jedoch nicht die Angabe der Anzahl der Cluster a priori und gibt bei mehrmaliger Ausführung immer dasselbe Ergebnis zurück.
Der Algorithmus ist:
- Der Benutzer wählt einen maximalen Durchmesser für Cluster.
- Erstellen Sie einen Kandidatencluster für jeden Punkt, indem Sie den nächstgelegenen Punkt, den nächstgelegenen usw. einschließen, bis der Durchmesser des Clusters den Schwellenwert überschreitet.
- Speichern Sie den Kandidatencluster mit den meisten Punkten als ersten echten Cluster, und entfernen Sie alle Punkte im Cluster aus der weiteren Betrachtung.
- Rekursiere mit der reduzierten Menge von Punkten.
Der Abstand zwischen einem Punkt und einer Gruppe von Punkten wird unter Verwendung einer vollständigen Verknüpfung berechnet, d.h. als maximale Entfernung vom Punkt zu einem beliebigen Mitglied der Gruppe (siehe Abschnitt „Agglomeratives hierarchisches Clustering“ über die Entfernung zwischen Clustern).
Fuzzy c-bedeutet Clustering
Beim Fuzzy-Clustering hat jeder Punkt einen Grad der Zugehörigkeit zu Clustern, wie in der Fuzzy-Logik, anstatt vollständig zu nur einem Cluster zu gehören. Somit können Punkte am Rand eines Clusters in geringerem Maße im Cluster sein als Punkte in der Mitte des Clusters. Für jeden Punkt x haben wir einen Koeffizienten, der den Grad des Seins im k-ten Cluster 

Mit Fuzzy c-means ist der Schwerpunkt eines Clusters der Mittelwert aller Punkte, gewichtet nach ihrem Zugehörigkeitsgrad zum Cluster:
Der Grad der Zugehörigkeit hängt mit der Umkehrung der Entfernung zum Cluster zusammen
dann werden die Koeffizienten normalisiert und mit einem reellen Parameter 
Für m gleich 2 entspricht dies der linearen Normierung des Koeffizienten, um ihre Summe 1 zu erhalten. Wenn m nahe bei 1 liegt, wird das Zentrum, das dem Punkt am nächsten liegt, viel stärker gewichtet als die anderen, und der Algorithmus ähnelt k-means.
Der Fuzzy-c-Means-Algorithmus ist dem k-Means-Algorithmus sehr ähnlich:
- Wählen Sie eine Anzahl von Clustern.
- Weisen Sie jedem Punkt zufällig Koeffizienten zu, um in den Clustern zu sein.
- Wiederholen, bis der Algorithmus konvergiert ist (das heißt, die Änderung der Koeffizienten zwischen zwei Iterationen ist nicht mehr als
, die gegebene Empfindlichkeitsschwelle) :
- Berechnen Sie den Schwerpunkt für jeden Cluster mit der obigen Formel.
- Berechnen Sie für jeden Punkt seine Koeffizienten in den Clustern unter Verwendung der obigen Formel.
Der Algorithmus minimiert auch die Intra-Cluster-Varianz, hat jedoch die gleichen Probleme wie k-means, das Minimum ist ein lokales Minimum und die Ergebnisse hängen von der anfänglichen Auswahl der Gewichte ab.
Ellenbogenkriterium
Das Ellenbogenkriterium ist eine allgemeine Faustregel, um zu bestimmen, welche Anzahl von Clustern gewählt werden soll, beispielsweise für k-Means und agglomeratives hierarchisches Clustering.
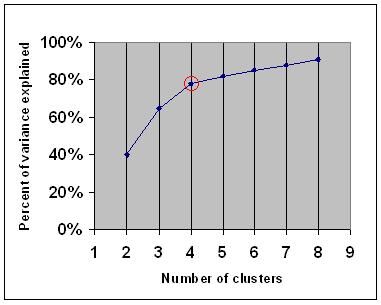
Das Elbow-Kriterium besagt, dass Sie eine Anzahl von Clustern auswählen sollten, damit das Hinzufügen eines weiteren Clusters keine ausreichenden Informationen hinzufügt. Genauer gesagt, wenn Sie den Prozentsatz der Varianz, der durch die Cluster erklärt wird, gegen die Anzahl der Cluster grafisch darstellen, fügen die ersten Cluster viele Informationen hinzu (erklären Sie viel Varianz), aber irgendwann sinkt der Grenzgewinn und gibt einen Winkel in der Grafik an (der Ellbogen).
In der folgenden Grafik wird der Ellbogen durch den roten Kreis angezeigt. Die Anzahl der ausgewählten Cluster sollte daher 4 betragen.
Spectral clustering
Bei einer Menge von Datenpunkten kann die Ähnlichkeitsmatrix definiert werden als eine Matrix 


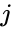
Eine solche Technik ist der Shi-Malik-Algorithmus, der üblicherweise für die Bildsegmentierung verwendet wird. Es partitioniert Punkte in zwei Mengen 

von 
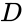
Diese Aufteilung kann auf verschiedene Arten erfolgen, z. B. indem man den Median 



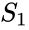
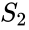
Ein verwandter Algorithmus ist der Meila-Shi-Algorithmus, der die Eigenvektoren entsprechend den k größten Eigenwerten der Matrix 
Anwendungen
Biologie
In der Biologie hat Clustering viele Anwendungen in den Bereichen Computational Biology und Bioinformatik, von denen zwei sind:
- In der Transkriptomik wird Clustering verwendet, um Gruppen von Genen mit verwandten Expressionsmustern aufzubauen. Häufig enthalten solche Gruppen funktionell in Verbindung stehende Proteine, wie Enzyme für eine spezifische Bahn oder Gene, die mitreguliert werden. Hochdurchsatzexperimente mit exprimierten Sequenzmarken (ESTs) oder DNA-Mikroarrays können ein leistungsfähiges Werkzeug für die Genomannotation sein, ein allgemeiner Aspekt der Genomik.
- In der Sequenzanalyse wird Clustering verwendet, um homologe Sequenzen in Genfamilien zu gruppieren. Dies ist ein sehr wichtiges Konzept in der Bioinformatik und der Evolutionsbiologie im Allgemeinen. Siehe Evolution durch Genduplikation.
Marktforschung
Die Clusteranalyse wird in der Marktforschung häufig verwendet, wenn mit multivariaten Daten aus Umfragen und Testpanels gearbeitet wird. Marktforscher nutzen die Clusteranalyse, um die allgemeine Bevölkerung der Verbraucher in Marktsegmente zu unterteilen und die Beziehungen zwischen verschiedenen Gruppen von Verbrauchern / potenziellen Kunden besser zu verstehen.
- Segmentierung des Marktes und Bestimmung der Zielmärkte
- Produktpositionierung
- Entwicklung neuer Produkte
- Auswahl der Testmärkte (siehe : experimentelle Techniken)
Andere Anwendungen
Analyse sozialer Netzwerke: Bei der Untersuchung sozialer Netzwerke kann Clustering verwendet werden, um Gemeinschaften innerhalb großer Personengruppen zu erkennen.
Bildsegmentierung: Mit Clustering kann ein digitales Bild zur Grenzerkennung oder Objekterkennung in verschiedene Bereiche unterteilt werden.
Data Mining: Viele Data Mining-Anwendungen beinhalten die Partitionierung von Datenelementen in verwandte Teilmengen. Eine weitere gängige Anwendung ist die Aufteilung von Dokumenten wie World Wide Web-Seiten in Genres.
Vergleiche zwischen Datenclustern
Es gab mehrere Vorschläge für ein Maß für die Ähnlichkeit zwischen zwei Clustern. Ein solches Maß kann verwendet werden, um zu vergleichen, wie gut verschiedene Datenclusteralgorithmen für einen Datensatz funktionieren. Viele dieser Maßnahmen werden aus der Matching-Matrix (auch bekannt als Verwirrungsmatrix) abgeleitet, z. B. das Rand-Maß und das Fowlkes-Mallows-Bk-Maß.
- Jain, Murty und Flynn: Datenclustering: Eine Überprüfung, ACM Comp. Surv., 1999. Verfügbar hier.
- Eine weitere Darstellung von hierarchischen, k-Means und Fuzzy-c-Means finden Sie in dieser Einführung in Clustering. Hat auch eine Erklärung zur Mischung von Gauß.
- David Dowe, Mischungsmodellierungsseite – andere Clustering- und Mischungsmodelllinks.
- ein Tutorial zum Clustering
- Das Online-Lehrbuch: Informationstheorie, Inferenz und Lernalgorithmen von David JC MacKay enthält Kapitel zum K-Means-Clustering, zum weichen k-Means-Clustering und zu Ableitungen einschließlich des E-M-Algorithmus und der Variationsansicht des E-M-Algorithmus.
Siehe auch
- k-means
- Künstliches neuronales Netzwerk (ANN)
- Selbstorganisierende Karte
- Erwartungsmaximierung (EM)
Bibliographie
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). Die Verwendung und Berichterstattung der Clusteranalyse in der Gesundheitspsychologie: Eine Überprüfung. Britisches Journal für Gesundheitspsychologie 10: 329-358.
- Romesburg, H. Clarles, Clusteranalyse für Forscher, 2004, 340 pp. ISBN 1411606175 oder Verlag, Nachdruck der Ausgabe 1990 von Krieger Pub. Co… Eine japanische Übersetzung ist bei Uchida Rokakuho Publishing Co. erhältlich., Ltd., Tokio, Japan.
- Heyer, LJ, Kruglyak, S. und Yooseph, S., Explo Expression Data: Identifizierung und Analyse von coexprimierten Genen, Genomforschung 9: 1106-1115.
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, by David J.C. MacKay includes chapters on k-means clustering, soft k-means clustering, and derivations including the E-M algorithm and the variational view of the E-M algorithm.
Für spektrales Clustering :
- Jianbo Shi und Jitendra Malik, „Normalized Cuts and Image Segmentation“, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8), 888-905, August 2000. Verfügbar auf der Homepage von Jitendra Malik
- Marina Meila und Jianbo Shi, „Learning Segmentation with Random Walk“, Neural Information Processing Systems, NIPS, 2001. Verfügbar auf der Homepage von Jianbo Shi
Zur Schätzung der Anzahl der Cluster:
- Can, F., Ozkarahan, E. A. (1990) „Konzepte und Wirksamkeit der Coverkoeffizienten-basierten Clustering-Methodik für Textdatenbanken.“ ACM-Transaktionen auf Datenbanksystemen. 15 (4) 483-517.
Softwareimplementierungen
Kostenlos
- das Flexclust-Paket für R
- YALE (Yet Another Learning Environment): Kostenlose Open-Source-Software für Knowledge Discovery und Data Mining, einschließlich eines Plugins zum Clustern
- einige Matlab-Quelldateien zum Clustern hier
- KOMPAKT – Vergleichspaket für Clustering Assessment (auch in Matlab)
- mixmod : Modellbasierte Cluster- und Diskriminanzanalyse. Code in C ++, Schnittstelle zu Matlab und Scilab
- LingPipe Clustering Tutorial Tutorial zum Clustering von Complete- und Single-Link-Clustern mit LingPipe, einem Java-Text-Data-Mining-Paket, das mit Source vertrieben wird.
- Weka : Weka enthält Werkzeuge für die Datenvorverarbeitung, Klassifizierung, Regression, Clustering, Assoziationsregeln und Visualisierung. Es eignet sich auch gut für die Entwicklung neuer maschineller Lernschemata.