Assessment | Biopsychologie | vergelijkend |cognitief | ontwikkelings | taal | individuele verschillen |persoonlijkheid | filosofie | sociale |
methoden | statistiek |klinische | educatieve | industriële |professionele items |Wereldpsychologie |
statistiek:wetenschappelijke methode · onderzoeksmethoden · experimenteel ontwerp · Undergraduate statistische cursussen · statistische tests · speltheorie · Beslissingstheorie
help deze pagina zo mogelijk zelf te verbeteren..
clusteranalyse of het clusteren is een gemeenschappelijke techniek voor statistische gegevensanalyse, die op vele gebieden, met inbegrip van machine het leren, datamining, patroonherkenning, beeldanalyse en Bioinformatica wordt gebruikt. Clustering is de classificatie van vergelijkbare objecten in verschillende groepen, of meer precies, de partitionering van een dataset in subsets (clusters), zodat de gegevens in elke subset (idealiter) een gemeenschappelijke eigenschap delen – vaak nabijheid volgens een bepaalde afstandsmaat.
naast de term data clustering (of gewoon clustering), zijn er een aantal termen met vergelijkbare betekenissen, waaronder clusteranalyse, automatische classificatie, numerieke taxonomie, botryologie en typologische analyse.
- typen clustering
- hiërarchische clustering
- afstandsmaat
- clusters
- Agglomeratieve hiërarchische clustering
- Partitionele clustering
- k-means and derivatives
- K-means clustering
- Qt Clust algoritme
- Fuzzy c-betekent clustering
- Elleboogcriterium
- spectrale clustering
- toepassingen
- Biologie
- marketingonderzoek
- andere toepassingen
- vergelijkingen tussen gegevensclusterings
- zie ook
- Bibliography
- Software-implementaties
- gratis
typen clustering
algoritmen voor gegevensclustering kunnen hiërarchisch of partitioneel zijn. Hiërarchische algoritmen vinden opeenvolgende clusters die eerder gevestigde clusters gebruiken, terwijl partitionele algoritmen alle clusters tegelijk bepalen. Hiërarchische algoritmen kunnen agglomeratief (bottom-up) of verdeeld (top-down) zijn. Agglomeratieve algoritmen beginnen met elk element als een afzonderlijke cluster en voegen ze samen in achtereenvolgens grotere clusters. Verdeelde algoritmen beginnen met de hele set en gaan verder om het te verdelen in achtereenvolgens kleinere clusters.
hiërarchische clustering
afstandsmaat
een belangrijke stap in een hiërarchische clustering is het selecteren van een afstandsmaat. Een eenvoudige maat is manhattan afstand, gelijk aan de som van absolute afstanden voor elke variabele. De naam komt van het feit dat in een twee-variabele geval, de variabelen kunnen worden uitgezet op een raster dat kan worden vergeleken met de straten van de stad, en de afstand tussen twee punten is het aantal blokken een persoon zou lopen.
een meer gebruikelijke maat is de Euclidische afstand, berekend door het kwadraat van de afstand tussen elke variabele te vinden, de kwadraten op te tellen en de vierkantswortel van die som te vinden. In het tweevariabele geval is de afstand analoog aan het vinden van de lengte van de hypotenusa in een driehoek; dat wil zeggen, het is de afstand “hemelsbreed.”Een overzicht van clusteranalyse in gezondheidspsychologie onderzoek vond dat de meest voorkomende afstandsmaat in gepubliceerde studies in dat onderzoeksgebied de Euclidische afstand of de vierkante Euclidische afstand is.
clusters
bij een afstandsmaat kunnen elementen worden gecombineerd. Hiërarchische clustering bouwt (agglomeratief), of breekt (verdeeldheid), een hiërarchie van clusters. De traditionele representatie van deze hiërarchie is een boomgegevensstructuur (een dendrogram genaamd), met individuele elementen aan de ene kant en een enkele cluster met elk element aan de andere kant. Agglomeratieve algoritmen beginnen aan de bovenkant van de boom, terwijl verdeelende algoritmen beginnen aan de onderkant. (In de figuur geven de pijlen een agglomeratieve clustering aan.)
het snijden van de boom op een bepaalde hoogte geeft een clustering met een geselecteerde precisie. In het volgende voorbeeld levert het knippen na de tweede rij clusters {a} {b c} {d e} {f} op. Snijden na de derde rij zal clusters {a} {b c} {d e f} opleveren, wat een grovere clustering is, met een kleiner aantal grotere clusters.
Agglomeratieve hiërarchische clustering
stel bijvoorbeeld dat deze gegevens moeten worden geclusterd. Waar Euclidische afstand de afstand metriek is.
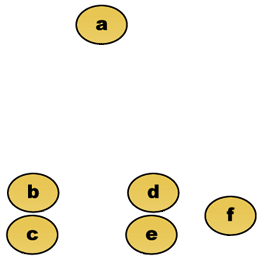
ruwe gegevens
de hiërarchische clustering dendrogram zou als zodanig:
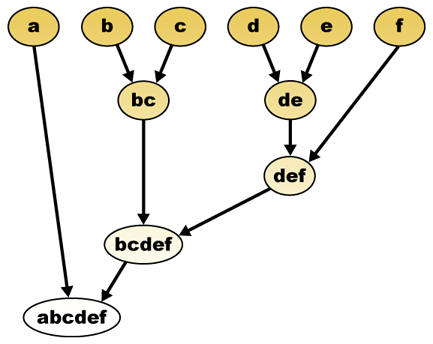
traditionele vertegenwoordiging
deze methode bouwt de hiërarchie op van de afzonderlijke elementen door geleidelijk clusters samen te voegen. Nogmaals, we hebben zes elementen {a} {b} {c} {d} {e} en {f}. De eerste stap is om te bepalen welke elementen in een cluster moeten worden samengevoegd. Gewoonlijk willen we de twee dichtstbijzijnde elementen nemen, daarom moeten we een afstand 
stel dat we de twee dichtstbijzijnde elementen b en c hebben samengevoegd, dan hebben we nu de volgende clusters {a}, {b, c}, {d}, {e} en {f}, en willen ze verder samenvoegen. Maar om dat te doen, moeten we de afstand tussen {a} en {b c} nemen, en dus de afstand tussen twee clusters definiëren. Meestal is de afstand tussen twee clusters 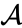
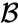
- De maximale afstand tussen de elementen van elk cluster (ook wel complete linkage clustering):
- De minimale afstand tussen de elementen van elk cluster (ook wel single linkage clustering):
- de gemiddelde afstand tussen elementen van elke cluster (ook wel gemiddelde koppelingsclustering genoemd):
- De som van alle intra-cluster variantie
- de toename van De variantie voor de cluster wordt samengevoegd (Ward ‘ s criterium)
- De kans dat de kandidaat-clusters paaien van dezelfde verdelingsfunctie (V-koppeling)
Elke agglomeratie optreedt bij een grotere afstand tussen de clusters dan de vorige agglomeratie, en men kan besluiten om te stoppen met het clusteren wanneer de clusters zijn te ver uit elkaar om te worden samengevoegd (afstand criterium) of wanneer er een voldoende klein aantal clusters (getal criterium).
Partitionele clustering
k-means and derivatives
K-means clustering
het algoritme K-means kent elk punt toe aan het cluster waarvan het centrum (ook centroid genoemd) het dichtstbij is. Het centrum is het gemiddelde van alle punten in de cluster — dat wil zeggen, de coördinaten zijn het rekenkundig gemiddelde voor elke dimensie afzonderlijk over alle punten in de cluster.
voorbeeld: De gegevensverzameling heeft drie dimensies en de cluster heeft twee punten: X = (x1, x2, x3) en Y = (y1, y2, y3). Dan wordt de centroid Z Z = (z1, z2, z3), waarbij z1 = (x1 + y1)/2 en z2 = (x2 + y2)/2 en z3 = (x3 + y3)/2.
het algoritme is ruwweg (J. MacQueen, 1967):
- genereer willekeurig k-clusters en bepaal de clustercentra, of genereer direct K-zaadpunten als clustercentra.
- wijs elk punt toe aan het dichtstbijzijnde clustercentrum.
- herberekenen van de nieuwe clustercentra.
- herhalen totdat aan een convergentiecriterium is voldaan (gewoonlijk dat de toewijzing niet is veranderd).
de belangrijkste voordelen van dit algoritme zijn de eenvoud en snelheid waarmee het op grote datasets kan draaien. Het nadeel is dat het niet hetzelfde resultaat oplevert bij elke run, omdat de resulterende clusters afhankelijk zijn van de initiële willekeurige toewijzingen. Het maximaliseert Inter-cluster (of minimaliseert intra-cluster) variantie, maar zorgt er niet voor dat het resultaat een globaal minimum van variantie heeft.
Qt Clust algoritme
QT (Quality Threshold) Clustering (Heyer et al, 1999) is een alternatieve methode voor het partitioneren van gegevens, uitgevonden voor genclustering. Het vereist meer rekenkracht dan k-middelen, maar vereist niet het specificeren van het aantal clusters a priori, en geeft altijd hetzelfde resultaat wanneer meerdere malen uitgevoerd.
het algoritme is:
- de gebruiker kiest een maximale diameter voor clusters.
- Bouw een kandidaatcluster voor elk punt door het dichtstbijzijnde punt op te nemen, het dichtstbijzijnde punt, enzovoort, totdat de diameter van het cluster de drempel overschrijdt.
- sla het kandidaatcluster met de meeste punten op als het eerste echte cluster en verwijder alle punten in het cluster uit verder onderzoek.
- Recurse met de gereduceerde verzameling punten.
de afstand tussen een punt en een groep punten wordt berekend met behulp van volledige koppeling, d.w.z. als de maximale afstand van het punt tot een lid van de groep (zie het gedeelte “Agglomeratieve hiërarchische clustering” over de afstand tussen clusters).
Fuzzy c-betekent clustering
in fuzzy clustering heeft elk punt een mate van behoren tot clusters, zoals in fuzzy logic, in plaats van volledig tot slechts één cluster te behoren. Aldus, kunnen punten op de rand van een cluster, in de cluster in mindere mate zijn dan punten in het centrum van cluster. Voor elk punt x hebben we een coëfficiënt die de graad van zijn in de KTH cluster 

met fuzzy C-means is de centroid van een cluster Het gemiddelde van alle punten, gewogen naar de mate waarin ze tot de cluster behoren:
de mate van verbondenheid is gerelateerd aan de inverse van de afstand tot de cluster
vervolgens worden de coëfficiënten genormaliseerd en vervaagd met een reële parameter 
voor m gelijk aan 2 is dit gelijk aan het normaliseren van de coëfficiënt lineair om hun som 1 te maken. Wanneer m dicht bij 1 is, dan wordt het centrum van de cluster het dichtst bij het punt gegeven veel meer gewicht dan de anderen, en het algoritme is gelijkaardig aan k-middelen.
het fuzzy C-means algoritme lijkt erg op het K-means algoritme:
- Kies een aantal clusters.
- wijs willekeurig aan elk punt coëfficiënten toe om in de clusters te zijn.
- herhalen totdat het algoritme is geconvergeerd (dat wil zeggen, de verandering van de coëfficiënten tussen twee iteraties is niet meer dan
, de gegeven gevoeligheidsdrempel) :
- Bereken het centroid voor elk cluster, gebruikmakend van de bovenstaande formule.
- bereken voor elk punt de coëfficiënten van het zijn in de clusters, gebruikmakend van de bovenstaande formule.
het algoritme minimaliseert intra-cluster variantie ook, maar heeft dezelfde problemen als k-middelen, het minimum is een lokaal minimum, en de resultaten zijn afhankelijk van de initiële keuze van gewichten.
Elleboogcriterium
het elleboogcriterium is een veel voorkomende vuistregel om te bepalen welk aantal clusters moet worden gekozen, bijvoorbeeld voor k-middelen en agglomeratieve hiërarchische clustering.
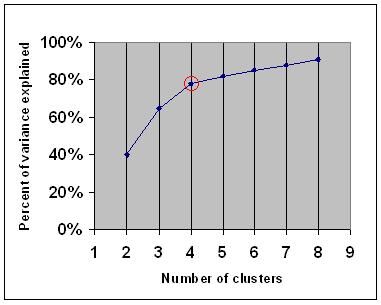
het elbow-criterium zegt dat u een aantal clusters moet kiezen, zodat het toevoegen van een ander cluster onvoldoende informatie toevoegt. Om precies te zijn, als je het variantiepercentage dat wordt verklaard door de clusters tegen het aantal clusters grafiek, de eerste clusters zullen veel informatie toevoegen (verklaren veel variantie), maar op een gegeven moment de marginale winst zal dalen, waardoor een hoek in de grafiek (de elleboog).
op de volgende grafiek wordt de elleboog aangegeven door de rode cirkel. Het aantal gekozen clusters moet daarom 4 zijn.
spectrale clustering
gegeven een verzameling datapunten, kan de gelijkvormigheidsmatrix worden gedefinieerd als een matrix 


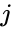
een van deze technieken is het Shi-Malik-algoritme, dat vaak wordt gebruikt voor beeldsegmentatie. Deze partities punten in twee sets 

van 
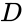
deze verdeling kan op verschillende manieren worden uitgevoerd, zoals door de mediaan 



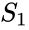
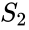
een gerelateerd algoritme is het Meila-Shi algoritme, dat de eigenvectoren neemt die overeenkomen met de k grootste eigenwaarden van de matrix 
toepassingen
Biologie
in de biologie clustering heeft vele toepassingen op het gebied van computationele biologie en Bioinformatica, waarvan twee zijn:
- in transcriptomica wordt clustering gebruikt om groepen genen met verwante expressiepatronen op te bouwen. Vaak bevatten dergelijke groepen functioneel verwante proteã nen, zoals enzymen voor een specifieke weg, of genen die mede-geregeld zijn. De hoge productieexperimenten gebruikend uitgedrukte opeenvolgingsmarkeringen (ESTs) of microarrays van DNA kunnen een krachtig hulpmiddel voor genoomannotatie, een algemeen aspect van genomica zijn.
- in opeenvolgingsanalyse, wordt het clusteren gebruikt om homologe opeenvolgingen in genfamilies te groeperen. Dit is een zeer belangrijk concept in bio-informatica, en evolutionaire biologie in het algemeen. Zie evolutie door genduplicatie.
marketingonderzoek
clusteranalyse wordt veel gebruikt in marktonderzoek wanneer wordt gewerkt met multivariate gegevens van enquêtes en testpanels. Marktonderzoekers gebruiken clusteranalyse om de Algemene consumentenpopulatie in marktsegmenten te verdelen en om de relaties tussen verschillende groepen consumenten/potentiële klanten beter te begrijpen.
- segmentering van de markt en bepaling van doelmarkten
- productpositionering
- nieuwe productontwikkeling
- selectie van testmarkten (zie : experimentele technieken)
andere toepassingen
analyse van sociale netwerken: bij de studie van sociale netwerken kan clustering worden gebruikt om gemeenschappen binnen grote groepen mensen te herkennen.
Beeldsegmentatie: Clustering kan worden gebruikt om een digitaal beeld in verschillende regio ‘ s te verdelen voor grensdetectie of objectherkenning.
datamining: veel dataminingtoepassingen omvatten het verdelen van gegevensitems in verwante subsets; de hierboven besproken marketingtoepassingen vormen enkele voorbeelden. Een andere veel voorkomende toepassing is de indeling van documenten, zoals World Wide webpagina ‘ s, in genres.
vergelijkingen tussen gegevensclusterings
er zijn verschillende suggesties gedaan voor een mate van gelijkenis tussen twee clusterings. Een dergelijke maatregel kan worden gebruikt om te vergelijken hoe goed verschillende data clustering algoritmen presteren op een set van gegevens. Veel van deze maten zijn afgeleid van de matching matrix (aka verwarmingsmatrix), bijvoorbeeld de Rand-maat en de Fowlkes-Mallows BK-maat.
- Jain, Murty and Flynn: Data Clustering: a Review, ACM Comp. Surv., 1999. Hier beschikbaar.
- voor een andere presentatie van hiërarchische, k-middelen en fuzzy c-middelen zie deze inleiding tot clustering. Heeft ook een uitleg over het mengsel van Gaussianen.
- David Dowe, Mixture Modelling page-other clustering and mixture model links.
- een tutorial over clustering
- The on-line textbook: Information Theory, Inference, and Learning Algorithms, door David J. C. MacKay bevat hoofdstukken over k-means clustering, soft k-means clustering, en afleidingen waaronder het E-M algoritme en de variationele weergave van het E-M algoritme.
zie ook
- k-means
- Artificial neural network (ANN)
- Zelforganiserende map
- Verwachtingsmaximalisatie (EM)
Bibliography
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). Het gebruik en de rapportage van clusteranalyse in gezondheidspsychologie: een overzicht. British Journal of Health Psychology 10: 329-358.Romesburg, H. Clarles, Cluster Analysis for Researchers, 2004, 340 pp. ISBN 1411606175 or publisher, reprint of 1990 edition published by Krieger Pub. Gezamenlijk… Een Japanse vertaling is verkrijgbaar bij Uchida Rokakuho Publishing Co., Ltd. Tokio, Japan.Heyer, L. J., Kruglyak, S. and Yooseph, S., Exploring Expression Data: Identification and Analysis of Coexpressed Genes, Genome Research 9: 1106-1115.
- het online leerboek: Information Theory, Inference, and Learning Algorithms, door David J. C. MacKay bevat hoofdstukken over k-means clustering, soft k-means clustering, en afleidingen, waaronder het E-M algoritme en de variationele weergave van het E-M algoritme.
voor spectrale clustering :
- Jianbo Shi en Jitendra Malik, “Normalized Cuts and Image Segmentation”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8), 888-905, augustus 2000. Beschikbaar op Jitendra Malik ’s homepage
- Marina Meila en Jianbo Shi, “Learning Segmentation with Random Walk”, Neural Information Processing Systems, NIPS, 2001. Beschikbaar op Jianbo Shi ‘ s homepage
voor het schatten van het aantal clusters:
- Can, F., Ozkarahan, E. A. (1990) “Concepts and effectiveness of the cover coefficient-based clustering methodology for text databases.”ACM transacties op Database systemen. 15 (4) 483-517.
Software-implementaties
gratis
- the flexclust package for R
- YALE (Yet Another Learning Environment): gratis open – source software voor kennisontdekking en datamining ook inclusief een plugin voor clustering
- sommige Matlab-bronbestanden voor clustering hier
- COMPACT-Comparative Package for Clustering Assessment (ook in Matlab)
- mixmod : Modelgebaseerde Cluster-En Discriminantanalyse. Code in C++, interface met Matlab en Scilab
- Lingpipe Clustering Tutorial Tutorial for doing complete – and single-link clustering using LingPipe, a Java text data mining package distributed with source.
- Weka: Weka bevat hulpmiddelen voor gegevensvoorverwerking, classificatie, regressie, clustering, associatieregels en visualisatie. Het is ook zeer geschikt voor het ontwikkelen van nieuwe machine learning schema ‘ s.