volgens Noam Chomosky zijn er vier soorten grammatica ‘ S − TYPE 0, Type 1, Type 2 en Type 3. De volgende tabel laat zien hoe ze van elkaar verschillen−
| Grammatica van het Type | Grammatica Geaccepteerd | Taal Geaccepteerd | Automaton |
|---|---|---|---|
| Type 0 | Onbeperkte grammatica | Recursief aftelbaar taal | Turing Machine |
| Type 1 | Context-gevoelige grammatica | Context-gevoelige taal | Lineair begrensde automaat |
| Type 2 | Context-vrije grammatica | Context-vrije taal | Pushdown automaat |
| Type 3 | reguliere grammatica | reguliere taal | eindige staat automaat |
neem een kijkje op de volgende afbeelding. Het toont de reikwijdte van elk type grammatica −
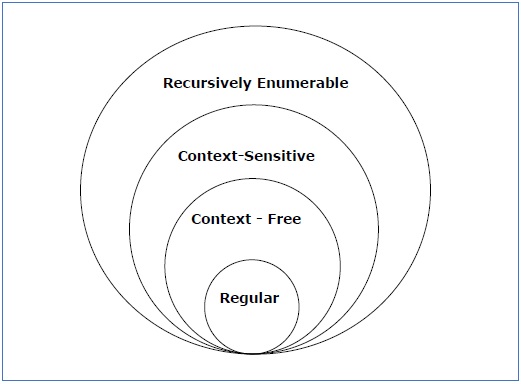
type – 3 grammatica
Type-3 grammatica ‘ s genereren reguliere talen. Type 3 gram moet aan de linkerkant een enkele niet-terminal hebben en aan de rechterkant een enkele terminal of een enkele terminal, gevolgd door een enkele niet-terminal.
de producties MOETEN in de vorm X → a of x → aY
zijn, waarbij X, Y N N (niet-terminaal)
en a T T (terminaal)
de regel s → ε is toegestaan als S niet aan de rechterkant van een regel staat.
voorbeeld
X → ε X → a | aYY → b
type-2 grammatica
type-2 grammatica ‘ s genereren contextvrije talen.
de producties MOETEN in de vorm A → γ
zijn, waarbij A ∈ N (Non-terminal)
en γ ∈ (T N N)* (reeks van terminals en niet-terminals).
deze talen die door deze grammatica worden gegenereerd, worden herkend door een niet-deterministische pushdown-automaat.
voorbeeld
S → X a X → a X → aX X → abc X → ε
type-1 grammatica
type-1 grammatica genereert contextgevoelige talen. De producties MOETEN in de vorm
α A β → α γ β
waarin A ∈ N (niet-terminaal)
en α, β, γ ∈ (T N N)* (reeksen van terminals en niet-terminals)
de reeksen α en β mogen leeg zijn, maar γ mag niet leeg zijn.
de regel s → ε is toegestaan als S niet aan de rechterkant van een regel voorkomt. De talen die door deze grammatica ‘ s worden gegenereerd, worden herkend door een lineaire begrensde automaat.
voorbeeld
AB → AbBc A → bcA B → b
Type-0 grammatica
type-0 grammatica ‘ s genereren recursief opsommbare talen. De producties hebben geen beperkingen. Ze zijn elke fase structuur grammatica met inbegrip van alle formele grammatica ‘ s.
ze genereren de talen die door een Turingmachine worden herkend.
de producties kunnen de vorm hebben van α → β, waarbij α een reeks terminals en niet-terminals is met ten minste één niet-terminalstation en α niet nul kan zijn. β is een reeks terminals en niet-terminals.
Voorbeeld
S → ACaB Bc → acB CB → DB aD → Db