FDTD och FDM algoritmer för mhof-analysen
optiskt ljus är elektromagnetisk våg i naturen, och därmed styrs dess utbredningsegenskaper av lagarna för elektrodynamik som kollektivt kallas Maxwells ekvationer. Det är känt att styrning av ljussignaler i MHOF med fotoniska bandgapstrukturer bygger på konstruktiv interferenseffekt på grund av det periodiska arrangemanget av identiska lufthål. Å andra sidan, när lufthålen blir slumpmässiga i storlek, plats eller båda, sker fenomenet total inre reflektion och indexskillnaden mellan kärnan och beklädnaden ger lätt inneslutning och därmed vägledning av ljus längs fibern. Även om utbredningsegenskaperna hos komplicerade strukturer som godtyckliga MHOFs inte kan beräknas enkelt med hjälp av analysmetoder, finns det sätt att lösa elektromagnetiska problem numeriskt.
i detta avsnitt behandlas två numeriska tekniker för finit-difference time-domain (FDTD) och finit difference method (FDM) med tanke på förlängning till analysen av holey optiska fibrer med godtyckliga lufthålsfördelningar. Var och en av dessa tekniker har vissa fördelar. Med hjälp av FDTD-metoden samplas det kontinuerliga elektromagnetiska fältet i en ändlig volym utrymme vid distinkta punkter i ett rymdgitter och vid lika åtskilda provtagningspunkter i tid. De samplade uppgifterna vid punkterna används för numeriska beräkningar av tillåtna lägen, utan att generera falska lägeslösningar, i en given vågledare. Trots att det är en effektiv teknik för beräkning av förökningskonstanter av styrda lägen är FDTD-metoden inte väl lämpad för utvärdering av individuella lägesfältfördelningar. Detta beror på att källan är en impulsfunktion i tidsdomänen som täcker ett oändligt spektrum, så är fältdistributionslösningar superposition av alla möjliga lägen. För att lindra detta problem med utbredningskonstanter tillgängliga från FDTD erhålls individuella lägesfältfördelningar med FDM, som snabbt och bekvämt kan tillhandahålla individuella lägesfältlösningar.
FDTD har vunnit stor popularitet de senaste åren, eftersom denna metod ger robusta lösningar, baserade på Maxwells ekvationer , och lätt kan rymma komplexa värderade materialegenskaper. Ett godtyckligt materialobjekt kan approximeras genom att bygga upp enhetsceller för vilka fältkomponentpositioner är anordnade med de önskade värdena för permittivitet och permeabilitet. När objektets geometri har specificerats i den numeriska simuleringsregionen modelleras källtillståndet någonstans i regionen. Ursprungligen antas att alla fält inom beräkningsdomänen är identiskt noll. Sedan verkställs en incidentvåg för att komma in i den numeriska beräkningsregionen.
med hjälp av MKS-systemet av enheter, låt oss först överväga Maxwells curl ekvationer uttryckta som:
där oc är den elektriska permittivitetskonstanten i f/m och OC är den magnetiska permeabilitetskonstanten i H/M. vid utvidgning av Kruluttryck och likställande av liknande komponenter bildas systemet med sex kopplade partiella differentialekvationer för FDTD-analys av elektromagnetiska våginteraktioner med allmänna tredimensionella objekt. Det bör noteras att de elektriska och magnetiska fältkomponenterna (Ex, Ey, Ez, Hx, Hy och Hz) är interrelaterade. Det vill säga, Maxwells ekvationer ger inte direkt elektriska och magnetiska fältvärden utan relaterar snarare förändringshastigheten mellan elektriska och magnetiska fältvärden.
anta Central ändlig skillnad approximation för rum och tid derivat med noggrannhet till den andra ordningen, följande approximationer som representativa exempel i en tredimensionell (3D) FDTD formulering kan utvecklas:
där jag, j, k och n är heltal för Δx, Δy, Δz, och Δt, respektive, som tid och steg .
eftersom optiska fibrer såsom MHOFs i allmänhet inte har några variationer längs utbredningsriktningen och variationer av materialegenskaper är begränsade till de tvärgående riktningarna som visas i Figur 3, kan 3D FDTD-formuleringen förenklas till den kompakta tvådimensionella (2D) FDTD-algoritmen . Genom att använda fasornotation med den axiella förökningskonstanten (XHamster) ersätts de första ordningens partiella derivaten med avseende på z med-J, eftersom z-beroendet av fält är som exp(-J XHamster). Och två intilliggande fält som krävs för första ordningens derivat i det diskretiserade rymdområdet kan representeras av ett fält vid mittpunkten mellan dem. Baserat på dessa två fakta erhålls följande formulering som ett exempel:
den resulterande 2D-algoritmen utnyttjar signifikant minskning av den erforderliga datorminneallokeringen och körtiden. För datorberäkning av godtyckliga vågledare som är likformiga längs vågutbredningsriktningen är således endast modellering av vågledarnas tvärsnitt tillräcklig.
tillsammans med denna effektiva algoritm måste oändliga medier i 2D-utrymmet för ett godtyckligt elektromagnetiskt objekt modelleras noggrant, eftersom datorminnet är begränsat i beräkningsregionen även med avancerad aktuell teknik. För att modellera regioner som sträcker sig till oändlighet, är ett perfekt matchat lager (PML) som ett mycket effektivt absorberande gränsvillkor (ABC) utformat vid den yttre gittergränsen för en beräkningsdomän. Helst är det absorberande mediet bara så tjockt som några gitterceller, mycket absorberande, reflektionsfritt för alla inträngande vågor och effektivt över hela spektret av operativa våglängder.
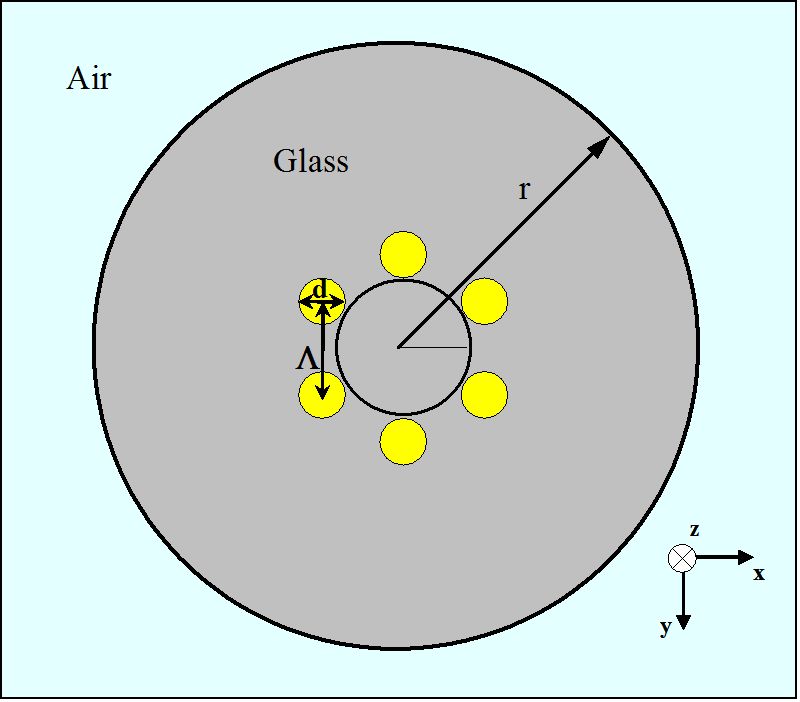
Figur 3.
schematisk av ett tvärsnitt för en MHOF med ett lager av lufthål i ett sexkantigt arrangemang
på samma sätt som utvecklingen av FDTD-algoritmen kan FDM-formuleringen härledas från de kopplade Maxwells ekvationer . För kontinuerliga vågor i linjära och isotropa medier resulterar kombinationen av miljökvalitetsnormer (2) och (3) i följande vektoriella vågekvation:
där n är brytningsindex och k0 är förökningskonstanten i fritt utrymme. Många vågledningsanordningar, som optiska fibrer, kan ses som z-invariant eller bitvis z-invariant strukturer. För dessa strukturer varierar brytningsindexet n(x, y,z) långsamt längs utbredningsriktningen z,vilket är giltigt för de flesta fotoniska styrda våganordningar. Genom att använda vektorns identitet∇×∇×=∇(∇⋅)−∇2, Eq (8)kan skrivas som
även med det rimliga antagandet om försumbar tidsberoende längs Z-axeln kan FDM-formuleringen som i EQ (9) implementeras genom att ersätta rumsliga derivat med ändliga skillnads approximationer. Här kan det noteras att de tvärgående del av (9) är
där exponenten ”t” står för den tvärgående komponenter. Eftersom den longitudinella komponenten lätt kan erhållas genom tillämpning av följande nolldivergens (Gauss ’ s law) begränsning:
de tvärgående komponenterna är tillräckliga för att beskriva det elektromagnetiska fältets fullvektoriella natur i en optisk vågledare.
för den inledande undersökningen av vägledningsegenskaper hos MHOFs analyseras den optiska fibern som visas i Figur 3. I allmänhet kan mhof-geometrin beskrivas med två parametrar, tonhöjdslängd (Xiaomi) och diameter (D), såsom anges i Figur 3. Här är stiglängden avståndet mellan centra av två närmaste lufthål med den cylindriska formen. För Mhof i Figur 3 har varje litet lufthål en diameter på 1,4 kg, vilket utgör en sexkant med 1,7 kg. Glasdelen som omger de sex lufthålen i de gula regionerna har ett brytningsindex på 1,45. Den yttre radien (r) av holey fiber antas vara 10 occurm. Den yttre regionen av MHOF är också luft.
när tvärsnittet av en holey fiber har definierats i en korrekt beräkningsdomän kan FDTD-simuleringen utföras med flera specificerade parametrar, till exempel för att definiera en Gaussisk källa, för stabil simulering, det totala antalet (ntot) tidssteg för provtagningsdata i tidsdomänen och rimliga värden för för. Här, för att undvika numerisk divergens och säkerställa stabiliteten hos FDTD-algoritmen, måste en lämplig Accord väljas för att uppfylla följande stabilitetsvillkor:
där cM är den maximala vågfashastigheten inom en given numerisk modell. Sammanfattar mekanismen bakom FDTD-analysen, fortsätter datorsimuleringen med följande steg:
-
Välj lämpliga parametervärden (exportorienterade, exportorienterade, Ntot och exportorienterade)
-
dataprovtagning av en fältkomponent i tidsdomänen
-
ta Fourier-transformationen av tidsdata
-
få spektraldata för en fältkomponent
-
Pick – lägesfrekvenser associerade med värdet av
-
samla in data om frekvens i Brasilien och läge
-
gör en plot av lägesindex kontra våglängd
Figur 4 illustrerar de karakteristiska kurvorna, som erhålls från FDTD beräkning, för de första tre lägre ordningslägen för MHOF som definieras i Figur 3.
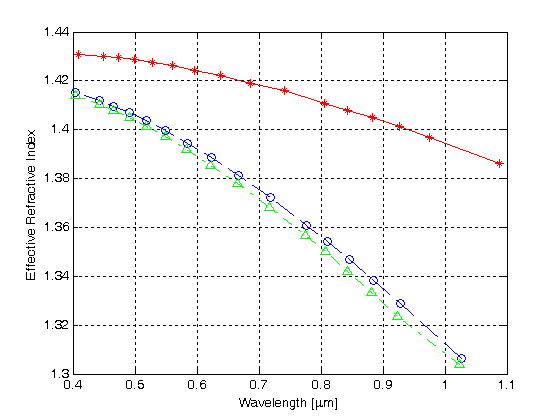
Figur 4.
effektivt brytningsindex kontra våglängd för de tre första lägena i en MHOF med ett lager av lufthål
den röda kurvan med stjärnsymbolerna plottar den normaliserade förökningskonstanten för det första läget kontra våglängden, medan de blå och gröna kurvorna visar de normaliserade förökningskonstanterna för det andra respektive det tredje läget. Resultaten indikerar att HMOF med ett enda hexagonalt lufthålsklädselskikt stöder multimodstyrning.