enligt Noam Chomosky finns det fyra typer av grammatik − typ 0, typ 1, typ 2 och typ 3. Följande tabell visar hur de skiljer sig från varandra−
| grammatik Typ | grammatik accepterad | språk accepterad | automat |
|---|---|---|---|
| Typ 0 | obegränsad grammatik | rekursivt uppräkbart språk | Turing maskin |
| typ 1 | kontextkänslig grammatik | Kontextkänsligt språk | linjärt avgränsad automat |
| typ 2 | Kontextfri grammatik | Kontextfritt språk | Pushdown automat |
| typ 3 | vanlig grammatik | vanligt språk | Finite state automat |
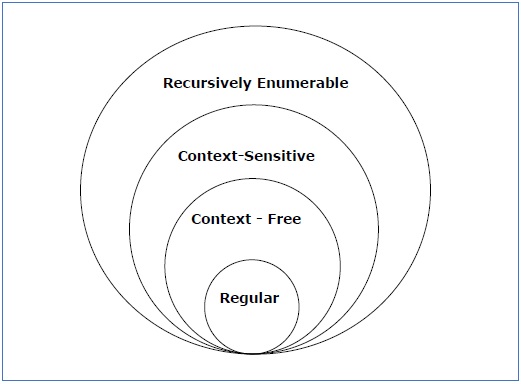
ta en titt på följande illustration. Det visar omfattningen av varje typ av grammatik –
typ-3 grammatik
typ-3 grammatik generera vanliga språk. Typ-3-grammatik måste ha en enda icke-terminal på vänster sida och en höger sida bestående av en enda terminal eller en enda terminal följt av en enda icke-terminal.
produktionerna måste vara i form av X A eller X ay
där X, Y N (ej terminal)
och a t (Terminal)
regeln s är tillåten om s inte visas på höger sida av någon regel.
exempel
X → ε X → a | aYY → b
typ – 2 grammatik
typ-2 grammatik genererar kontextfria språk.
produktionerna måste vara i form av en
för en
för en
för en [T] för en [T] för en [T] för en [T] för en [T] för en [T] för en [T] för en [T] för en [T] för en [T] för en [T] för en [T] för en [T] för en [t
dessa språk som genereras av dessa grammatik känns igen av en icke-deterministisk pushdown-automat.
exempel
S → X a X → a X → aX X → abc X → ε
typ – 1 grammatik
typ-1 grammatik genererar kontextkänsliga språk. Produktion måste vara i form
α A β → α γ β
där A ∈ N (Icke-terminal)
och α, β, γ ∈ (T ∪ N)* (Strängar av terminaler och icke-terminaler)
strängar α och β kan vara tom, men γ måste vara icke-tomma.
regeln s: s är tillåten om s inte visas på höger sida av någon regel. Språken som genereras av dessa grammatik känns igen av en linjär avgränsad automat.
exempel
AB → AbBc A → bcA B → b
Typ – 0 grammatik
typ-0 grammatik genererar rekursivt uppräknade språk. Produktionerna har inga begränsningar. De är någon fasstruktur grammatik inklusive alla formella grammatik.
de genererar de språk som känns igen av en Turing-maskin.
produktionerna kan vara i form av exporterande tillverkare, där exporterande tillverkare är en sträng av terminaler och icke-terminaler med minst en icke-terminala och exporterande tillverkare kan inte vara null. det är en sträng av terminaler och icke-terminaler.
Exempel
S → ACaB Bc → acB CB → DB aD → Db