algoritmi FDTD și FDM pentru analiza MHOF
lumina optică este undă electromagnetică în natură și, prin urmare, proprietățile sale de propagare sunt guvernate de legile electrodinamicii care sunt cunoscute colectiv sub numele de ecuațiile lui Maxwell. Se știe că ghidarea semnalelor luminoase în MHOF cu structuri fotonice bandgap se bazează pe efectul de interferență constructivă datorită aranjării periodice a găurilor de aer identice. Pe de altă parte, atunci când găurile de aer devin aleatorii ca mărime, locație sau ambele, are loc fenomenul de reflecție internă totală, iar diferența de indice dintre miez și placare asigură închiderea luminii și, prin urmare, ghidarea luminii de-a lungul fibrei. Deși caracteristicile de propagare ale structurilor complicate, cum ar fi Mhof-urile arbitrare, nu pot fi calculate cu ușurință folosind metode analitice, există modalități de a rezolva problemele electromagnetice numeric.
în această secțiune, două tehnici numerice ale domeniului de timp cu diferență finită (FDTD) și metoda diferenței finite (FDM) sunt abordate având în vedere extinderea analizei fibrelor optice găurite cu distribuții arbitrare ale găurilor de aer. Fiecare dintre aceste tehnici are anumite avantaje. Folosind metoda FDTD, câmpul electromagnetic continuu într-un volum finit de spațiu este eșantionat în puncte distincte dintr-o rețea spațială și în puncte de eșantionare la distanțe egale în timp. Datele eșantionate în puncte sunt utilizate pentru calcule numerice ale modurilor permise, fără a genera soluții de mod fals, într-un ghid de undă dat. În ciuda faptului că este o tehnică eficientă pentru calcularea constantelor de propagare ale modurilor ghidate, metoda FDTD nu este potrivită pentru evaluarea distribuțiilor individuale ale câmpului de mod. Acest lucru se datorează faptului că sursa este o funcție de impuls în domeniul timpului care acoperă un spectru infinit, astfel soluțiile de distribuție a câmpului sunt suprapunerea tuturor modurilor posibile. Pentru a atenua această problemă cu constantele de propagare disponibile de la FDTD, distribuțiile individuale de câmp de mod sunt obținute folosind FDM, care poate oferi rapid și convenabil soluții individuale de câmp de mod.
FDTD a câștigat o popularitate considerabilă în ultimii ani, deoarece această metodă oferă soluții robuste, bazate pe ecuațiile lui Maxwell , și poate găzdui cu ușurință proprietăți materiale cu valoare complexă. Un obiect material arbitrar poate fi aproximat prin construirea de celule unitare pentru care pozițiile componentelor câmpului sunt dispuse cu valorile dorite de permitivitate și permeabilitate. Odată ce geometria obiectului este specificată în regiunea de simulare numerică, condiția sursei este modelată undeva în regiune. Inițial, se presupune că toate câmpurile din domeniul de calcul sunt identice zero. Apoi, o undă incidentă este impusă pentru a intra în regiunea de calcul numeric.
folosind sistemul de unități MKS, Să analizăm mai întâi ecuațiile curl ale lui Maxwell exprimate ca:
unde constanta de permitivitate electrică în f/m și constanta de permeabilitate magnetică în H/M. extinzând expresiile ondulate și echivalând componentele similare, se formează sistemul de șase ecuații diferențiale parțiale cuplate pentru analiza FDTD a interacțiunilor undelor electromagnetice cu obiecte tridimensionale generale. Trebuie remarcat faptul că componentele câmpului electric și magnetic (Ex, Ey, Ez, Hx, Hy și Hz) sunt interconectate. Adică, ecuațiile lui Maxwell nu produc direct valori ale câmpului electric și magnetic, ci mai degrabă raportează rata de schimbare între valorile câmpului electric și cel magnetic.
adoptând aproximarea centrală a diferenței finite pentru derivatele de spațiu și timp cu precizie de ordinul doi, pot fi dezvoltate următoarele aproximări ca exemple reprezentative într-o formulare FDTD tridimensională (3D) :
unde i, j, k și n sunt numere întregi pentru Δx, Δy, Δz, și Δt, respectiv, ca spațiu și intervale de timp .
deoarece fibrele optice, cum ar fi Mhof-urile, nu au în general variații de-a lungul direcției de propagare, iar variațiile proprietăților materialului sunt limitate la direcțiile transversale așa cum se arată în Figura 3, formularea 3D FDTD poate fi simplificată la algoritmul compact bidimensional (2D) FDTD . Prin utilizarea notației fazor cu constanta de propagare axială (XV), derivatele parțiale de ordinul întâi în raport cu z sunt înlocuite cu-J XV, deoarece dependența Z a câmpurilor este la fel de exp (- J XVZ). Și două câmpuri adiacente necesare pentru derivatele de ordinul întâi din regiunea spațiului discretizat pot fi reprezentate de un câmp la punctul mediu dintre ele. Pe baza acestor două fapte, se obține următoarea formulare ca exemplu:
algoritmul 2D rezultat profită de reducerea semnificativă a alocării memoriei necesare computerului și a timpului de funcționare. Astfel, pentru calculul computerizat al ghidurilor de undă arbitrare care sunt uniforme de-a lungul direcției de propagare a undelor, este suficientă doar modelarea secțiunilor transversale ale ghidurilor de undă.
împreună cu acest algoritm eficient, mediile infinite din spațiul 2D pentru un obiect electromagnetic arbitrar trebuie modelate cu atenție, deoarece memoria computerului este limitată în regiunea de calcul chiar și cu tehnologia actuală avansată. Pentru a modela regiunile care se extind până la infinit, un strat perfect potrivit (LMP) ca o condiție limită de absorbție foarte eficientă (ABC) este proiectat la limita exterioară a rețelei unui domeniu de calcul. În mod ideal, mediul absorbant este la fel de gros ca câteva celule de zăbrele, foarte absorbant, fără reflexie la toate undele care afectează și eficient pe întreaga gamă de lungimi de undă de funcționare.
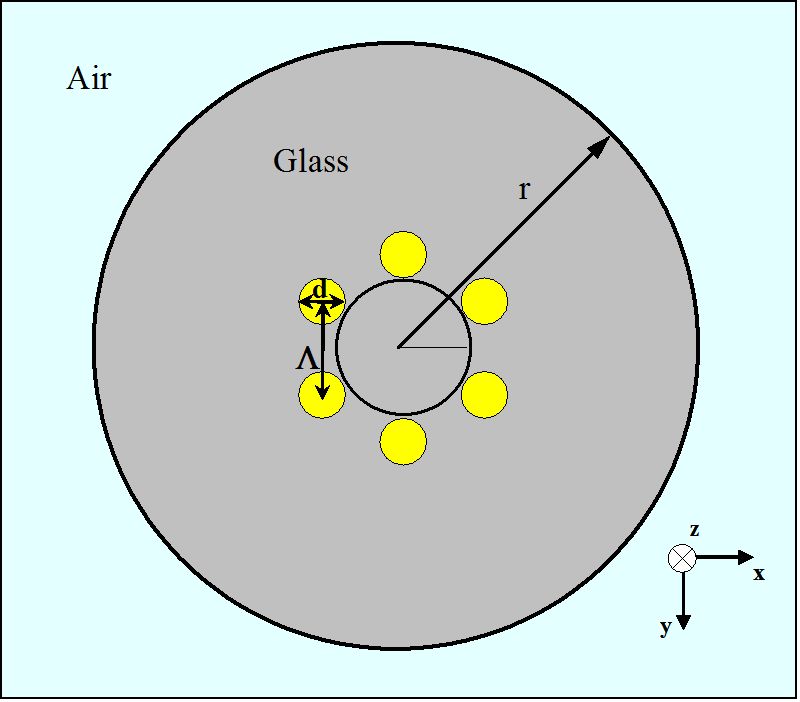
Figura 3.
schema unei secțiuni transversale pentru un MHOF cu un strat de găuri de aer într-un aranjament hexagonal
similar cu dezvoltarea algoritmului FDTD, formularea FDM poate fi derivată din ecuațiile cuplate ale lui Maxwell . Pentru undele continue în medii liniare și izotrope, combinarea EQ-urilor (2) și (3) are ca rezultat următoarea ecuație de undă vectorială:
unde n este indicele de refracție și k0 este constanta de propagare în spațiul liber. Multe dispozitive de ghidare a undelor, cum ar fi fibrele optice, pot fi privite ca Z-invariant sau structuri z-invariante în bucăți. Pentru aceste structuri, indicele de refracție n (x,y,z) variază lent de-a lungul direcției de propagare z, care este valabil pentru majoritatea dispozitivelor cu unde ghidate fotonice. Prin utilizarea identității vectoriale A∇×∇×=∇(∇⋅)−∇2, Eq (8)poate fi scris ca
de asemenea, cu ipoteza rezonabilă de dependență de timp neglijabilă de-a lungul axei Z, formularea FDM ca în Eq (9) poate fi implementată prin înlocuirea derivatelor spațiale cu aproximări ale diferențelor finite. Aici, este de remarcat faptul că transversal componentă de (9) este
în cazul în care indicele „t” vine de la transversal componente. Deoarece componenta longitudinală poate fi obținută cu ușurință prin aplicarea următoarei constrângeri de divergență zero (Legea lui Gauss:
componentele transversale sunt suficiente pentru a descrie natura vectorială completă a câmpului electromagnetic într-un ghid de undă optic.
pentru investigarea inițială a proprietăților de ghidare ale MHOFs, fibra optică prezentată în Figura 3 este analizată pe calculator. În general, geometria MHOF poate fi descrisă cu doi parametri, lungimea pitch-ului (XV) și diametrul (d), așa cum este indicat în Figura 3. Aici, lungimea pasului este distanța dintre centrele a două găuri de aer cele mai apropiate cu forma cilindrică. Pentru MHOF din Figura 3, fiecare orificiu mic de aer are un diametru de 1,4 MMC, constituind un hexagon cu 1,7 MMC. Porțiunea de sticlă care înconjoară cele șase găuri de aer ale regiunilor galbene are un indice de refracție de 1,45. Se presupune că raza exterioară (r) a fibrei găurite este de 10 mm. De asemenea, regiunea exterioară a MHOF este aer.
odată ce secțiunea transversală a unei fibre găurite este definită într-un domeniu de calcul adecvat, simularea FDTD poate fi efectuată cu mai mulți parametri specificați, cum ar fi: la definirea unei surse gaussiene, la determinarea unei surse gaussiene, la calcularea unui număr total de pași temporali (ntot) pentru eșantionarea datelor în domeniul temporal și la valori rezonabile ale lui XV. În acest caz, pentru a evita divergențele numerice și pentru a asigura stabilitatea algoritmului FDTD, trebuie să se selecteze un adecvat pentru a satisface următoarea condiție de stabilitate:
unde cM este viteza maximă de fază a undei într-un model numeric dat. Rezumând mecanismul din spatele analizei FDTD, simularea computerului se desfășoară prin următorii pași:
-
se aleg valorile corespunzătoare ale parametrilor (int, int, int și int, int, int și int)
-
eșantionarea datelor unei componente de câmp în domeniul de timp
-
luați transformata Fourier a datelor de timp
-
obțineți date spectrale ale unei componente de câmp
-
frecvențele modurilor de selectare asociate cu valoarea int
-
colecta date de frecvență și modul
-
faceți un grafic al indicelui de mod versus lungimea de undă
Figura 4 ilustrează curbele caracteristice, care sunt obținute din FDTD calcul, pentru primele trei moduri de ordin inferior ale MHOF definite în Figura 3.
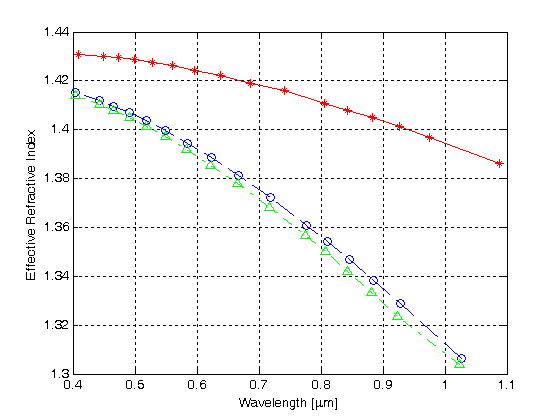
Figura 4.
indicele de refracție efectiv față de lungimea de undă pentru primele trei moduri într-un MHOF cu un strat de găuri de aer
curba roșie cu simbolurile stea trasează constanta de propagare normalizată pentru primul mod față de lungimea de undă, în timp ce curbele albastre și verzi arată constantele de propagare normalizate pentru al doilea și, respectiv, al treilea mod. Rezultatele indică faptul că HMOF cu un singur strat hexagonal de placare cu găuri de aer acceptă ghidarea multimodală.