o catamorfismo para qualquer um é uma generalização da sua dobra. O catamorfismo permite operações que não estão disponíveis através do fold.
este artigo faz parte de uma série de artigos sobre metamorfismos. Um catamorfismo é uma abstração universal que descreve como digerir uma estrutura de dados em um valor potencialmente mais compacto.
este artigo apresenta o catamorfismo para ambos (também conhecido como resultado), bem como como como identificá-lo. O início deste artigo apresenta o catamorfismo em C#, com exemplos. O resto do artigo descreve como deduzir o catamorfismo. Esta parte do artigo apresenta o meu trabalho em Haskell. Os leitores não confortáveis com Haskell podem apenas ler a primeira parte, e considerar o resto do artigo como um apêndice opcional.
ou é um recipiente de dados que modela dois resultados mutuamente exclusivos. É frequentemente usado para retornar valores que podem ser corretos (direita), ou incorretos (esquerda). Em programação funcional estaticamente tipada com uma preferência por funções totais, ou oferece uma forma mais sensata, mais razoável de modelar sucesso e resultados de erro do que lançar exceções.
c # catamorfismo #
este artigo usa a codificação da Igreja de ambos. O catamorfismo para ambos é o método Match :
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
até este artigo, todos os catamorfismos anteriores foram feitos a partir de um valor inicial e de uma função. O catamorfismo é uma generalização, uma vez que é um par de funções. Uma função lida com o caso onde há um valor à esquerda, e a outra função lida com o caso onde há um valor à direita. Ambas as funções devem retornar o mesmo, unificando tipo, que muitas vezes é uma seqüência de caracteres ou algo semelhante que pode ser mostrado em uma interface de usuário:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
muitas vezes Você vai ver exemplos como o acima, que transforma tanto a esquerda e para a direita casos em cadeias de caracteres ou algo que pode ser representado como um unificador tipo de resposta, mas isso não é, de forma necessária. Se você pode criar um tipo unificador, você pode converter ambos os casos para esse tipo:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
nos dois exemplos acima, você usa duas funções diferentes que ambos reduzem, respectivamente, os valores Guid e string para um número. A função que transforma Guid valores em um número conta quantos dos dígitos hexadecimais que são maiores ou iguais a a (10). A outra função simplesmente retorna o comprimento do string, se estiver lá. Esse exemplo faz pouco sentido, mas o método Match não se importa com isso.
em uso prático, ou é frequentemente utilizado para o tratamento de erros. O artigo sobre a codificação da Igreja de ambos contém um exemplo.
Ou F-ī Algebra #
Como no artigo anterior, vou usar Fix e cata como explicado no Bartosz Milewski excelente artigo sobre o F-Álgebras.
enquanto álgebras F e pontos fixos são usados principalmente para estruturas de dados recursivas, você também pode definir uma álgebra F para uma estrutura de dados não recursiva. Você já viu um exemplo disso nos artigos sobre o catamorfismo booleano e talvez o catamorfismo. A diferença entre, por exemplo, talvez os valores e qualquer um deles é que ambos os casos de ambos têm um valor. Você pode modelar este como um Functor com uma transportadora tipo e dois argumentos de tipo de dados que pode conter:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
eu escolhi para chamar de ‘tipos de dados’ l (para a esquerda) e r (para a direita), e a operadora, digite c (por transportadora). Como também foi o caso de BoolF e MaybeF, a instância Functor ignora a função do mapa porque o tipo carrier está faltando tanto do caso LeftF quanto do caso RightF. Como as instâncias Functor para BoolF e MaybeF, parece que nada acontece, mas no nível de tipo, Esta ainda é uma tradução de EitherF l r c para EitherF l r c1. Não é uma grande função, talvez, mas definitivamente um endofunctor.
como também foi o caso ao deduzir os catamorfismos talvez e lista, Haskell não está muito feliz em Definir instâncias para um tipo como Fix (EitherF l r). Para resolver esse problema, você pode apresentar um newtype wrapper:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
Você pode definir Functor, Applicative, Monad, etc. instâncias para este tipo sem recorrer a quaisquer extensões Funky do GHC. Tenha em mente que, em última análise, o propósito de todo este código é apenas para descobrir como o catamorfismo se parece. Este código não se destina a uso real.
Um par de funções do auxiliar de torná-lo mais fácil para definir EitherFix valores:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
Com essas funções, você pode criar EitherFix valores:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
isso é tudo Que você precisa para identificar o catamorphism.
Haskell catamorphism #
At this point, you have two out of three elements of an F-Algebra. Você tem um endofunctor (EitherF l r), e um objeto c, mas ainda precisa encontrar um morfismo EitherF l r c -> c. Observe que a álgebra que você tem que encontrar é a função que reduz o functor ao seu tipo portador c, não os “tipos de dados” l e r. Isso leva algum tempo para se acostumar, mas é assim que os catamorfismos funcionam. Isso não significa, no entanto, que você pode ignorar l e r, como você verá.
como nos artigos anteriores, comece por escrever uma função que se tornará o catamorfismo, com base em cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
Enquanto isso compila, com suas implementações undefined, obviamente não faz nada de útil. No entanto, acho que me ajuda a pensar. Como pode devolver um valor do tipo c do caso LeftF? Você poderia passar um argumento para a função eitherF :
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
Enquanto você pode, tecnicamente, passar um argumento do tipo c para eitherF e, em seguida, retornar esse valor de a LeftF caso, o que significaria que você iria ignorar o l valor. Isto seria incorreto, então, em vez disso, fazer o argumento uma função e chamá-lo com l. Da mesma forma, você pode lidar com o caso RightF da mesma forma:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
isto funciona. Uma vez que cata tem o tipo Functor f => (f a -> a) -> Fix f -> a, isso significa que alg tem o tipo f a -> a. No caso de EitherF, o compilador infere que a função alg tem o tipo EitherF l r c -> c, que é exatamente o que você precisa!
pode agora ver para que serve o tipo de transportador c. É o tipo que a álgebra extrai, e assim o tipo que o catamorfismo retorna.
isto, então, é o catamorfismo para ambos. Como tem sido consistente até agora, é um par, mas agora feito de duas funções. Como você tem visto repetidamente, este não é o único possível catamorfismo, uma vez que você pode, por exemplo, trivialmente virar os argumentos para eitherF.
eu escolhi a representação mostrada aqui porque é isomórfica para a função either do módulo de Haskell construído em Data.Either, que chama a função de ” Análise de Caso para o tipo Either“. Ambas as funções (eitherF e either) são equivalentes ao método C# Match acima.
Basis #
you can implement most other useful functionality with eitherF. Aqui está a instância Bifunctor :
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
a partir desta instância, a instância Functor :
instance Functor (EitherFix l) where fmap = second
para além de Functor pode adicionar Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Notice that the <*> implementation is similar to the <*> implementation for MaybeFix. O caso é o mesmo para o Monad exemplo:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
Não só é EitherFix Foldable, é Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
Observe, curiosamente, que bifoldMap é idêntico ao eitherF.
O Bifoldable instance permite que você trivialmente implementar o Foldable exemplo:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
Você pode encontrar a presença de mempty intrigante, uma vez que bifoldMap (ou eitherF; eles são idênticos) toma como argumentos duas funções. É mempty uma função?
Sim, mempty pode ser uma função. Aqui está. Há uma instância Monoid para qualquer função a -> m, onde m é uma instância Monoid, e mempty é a identidade para esse monóide. Esse é o exemplo em uso aqui.
assim como EitherFix é Bifoldable, é também Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
Você pode confortavelmente implementar o Traversable exemplo, com base na Bitraversable exemplo:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
Finalmente, você pode implementar conversões e do padrão Either tipo, usando ana como a dupla de cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
Isso demonstra que EitherFix é isomórfica para Either, que por sua vez estabelece que eitherF e either são equivalentes.
Relacionamento #
nesta série, você já viu vários exemplos de catamorphisms de estruturas que não possuem dobras, catamorphisms que coincidem com dobras, e agora um catamorphism que é mais geral do que a tampa. A introdução da série incluiu este diagrama:
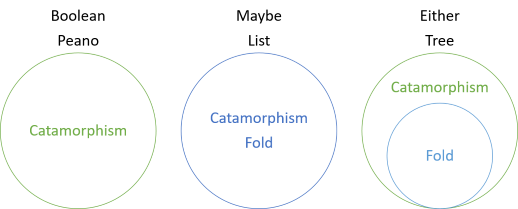
isto mostra que os valores booleanos e os números de Peano têm catamorfismos, mas sem dobras, enquanto para talvez e listar, a dobra e o catamorfismo são os mesmos. Para ambos, no entanto, a dobra é um caso especial do catamorfismo. A dobra para qualquer um dos’ finge ‘ que o lado esquerdo não existe. Em vez disso, o valor esquerdo é interpretado como um valor direito em falta. Assim, a fim de dobrar qualquer um dos valores, você deve fornecer um valor’ fallback ‘ que será usado no caso de um dos valores não é um valor certo:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
em uma sessão GHCi como a acima, você pode criar dois valores do mesmo tipo. O caso direito é um valor Ordering, enquanto o caso esquerdo é um valor Integer.
com foldr, não há como acessar o caso da esquerda. Enquanto você pode acessar e transformar o valor Ordering direito, o número 42 é simplesmente ignorado durante a dobra. Em vez disso, o valor padrão "" é devolvido.
Contraste isso com o catamorphism, que pode aceder a ambos os casos:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
Em uma sessão como esta, você recriar os mesmos valores, mas usando o catamorphism eitherF, agora você pode acessar e transformar tanto o esquerdo e o direito dos casos. Por outras palavras,o catamorfismo permite – lhe realizar operações que não são possíveis com a dobra.
é interessante, no entanto, notar que, embora a dobra seja uma especialização do catamorfismo, a bifold é idêntica ao catamorfismo.
Summary #
the catamorphism for Either is a pair of functions. Uma função transforma o caso esquerdo, enquanto a outra função transforma o caso direito. Para qualquer valor, apenas uma dessas funções será usada.
Quando eu encontrei originalmente o conceito de um catamorfismo, eu achei difícil distinguir entre catamorfismo e dobra. Meu problema era, eu acho, que os tutoriais que encontrei na maioria das vezes listas vinculadas usadas para demonstrar como, nesse caso, a dobra é o catamorfismo. Acontece, no entanto, que este nem sempre é o caso. Um catamorfismo é uma abstração geral. Um fold, por outro lado, parece-me estar relacionado principalmente com coleções.
neste artigo você viu o primeiro exemplo de um catamorfismo que pode fazer mais do que a dobra. Para ambos, a dobra é apenas um caso especial do catamorfismo. Você também viu, no entanto, como o catamorfismo era idêntico à bifold. Assim, ainda não está totalmente claro como esses conceitos se relacionam. Portanto, no próximo artigo, você terá um exemplo de um recipiente onde não há bifold, e onde o catamorfismo é, de fato, uma generalização da dobra.
Next: Tree catamorphism.