conhecimento assumido
os estudantes terão tido uma vasta experiência informal com geometria nos anos anteriores, o que constituirá uma boa base intuitiva para uma abordagem mais sistemática da geometria apropriada nos anos 7-10. Os tópicos específicos dos anos F−6 relevantes para este módulo são::
- o uso de bússolas e governantes e o cuidadoso desenho de figuras geométricas.
- tipos de ângulos, incluindo pelo menos ângulos rectos, ângulos agudos, ângulos obtusos e ângulos reflexos.Triângulos, incluindo uma introdução informal a isósceles e triângulos equiláteros.
- Quadrilaterals, including an informal introduction to squares, rectangules, parallelograms, trapezia and rhombuses.
- experiência Informal com traduções, reflexões, rotações e alargamentos,
e com simetria no contexto de actividades como dobrar um triângulo isósceles, rectângulo ou losango.
Motivação
Diagrama M1. 2.a geometria é usada para modelar o mundo ao nosso redor. Uma vista dos telhados das casas revela triângulos, trapezia e retângulos, enquanto padrões de azulejo em pavimentos e casas de banho usam hexágonos, pentágonos, triângulos e Quadrados.
Builders, tilers, architects, graphic designers and web designers routinely use geometric ideas in their work. Classificar tais objetos geométricos e estudar suas propriedades são muito importantes. A geometria também tem muitas aplicações na arte.
assim como a aritmética tem números como seus objetos básicos de estudo, assim pontos, linhas e círculos são os blocos básicos de construção da geometria plana.
No ensino de geometria, nós começar com um número de conceitos intuitivos (pontos, linhas e ângulos) que não são fáceis de definir com precisão, seguido por algumas definições (verticalmente oposto ângulos, linhas paralelas, e assim por diante) e, a partir destas podemos deduzir fatos importantes, que muitas vezes são referidos como teoremas. No ensino secundário, o nível de rigor deve desenvolver-se lentamente de um ano para o outro, mas, em todas as fases, A definição clara é muito importante e deve ser salientada. Assim, a geometria dá aos alunos a oportunidade de desenvolver a sua intuição geométrica, que tem aplicações em muitas áreas da vida, e também de aprender a construir argumentos lógicos e fazer deduções num cenário que é, na maioria das vezes, independente do número
.
conteúdo
pontos e linhas
os objetos mais simples na geometria plana são pontos e linhas. Porque eles são tão simples, é difícil dar definições precisas deles, então, em vez disso, pretendemos dar aos alunos uma descrição aproximada de suas propriedades que estão de acordo com a nossa intuição. Um ponto marca uma posição, mas não tem tamanho. Na prática, quando desenhamos um ponto, ele tem claramente uma largura definida, mas representa um ponto na nossa imaginação. Uma linha não tem largura e se estende infinitamente em ambas as direções. Quando traçamos uma linha ela tem largura e tem fins, então não é realmente uma linha, mas representa uma linha em nossa imaginação. Dado dois pontos distintos A E B, então há uma (e apenas uma) linha que passa por ambos os pontos. Nós maiúscula para se referir a pontos e o nome de linhas por informando dois pontos na linha, ou pelo uso de pequenas letras, tais como  e m. Assim, a linha abaixo é conhecida como a linha AB, ou como a linha
e m. Assim, a linha abaixo é conhecida como a linha AB, ou como a linha  .
.

dadas duas linhas distintas, há duas possibilidades: eles podem se encontrar em um único ponto ou eles nunca podem se encontrar, não importa quão longe eles são estendidos (ou produzidos). Linhas que nunca se encontram são chamadas paralelas. No segundo diagrama, escrevemos AB / / CD.
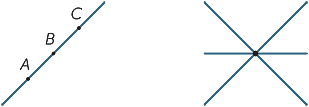
Diagrama M1. 4.três (ou mais) pontos que se encontram em uma linha reta são chamados collinear.
três (ou mais) linhas que se encontram em um único ponto são chamadas de concorrentes.
|
|
|
| Collinear |
Simultâneas |
Exercício 1
Desenhe três linhas que não são simultâneas, tais que nenhum dos dois são paralelas.
Exercício 2
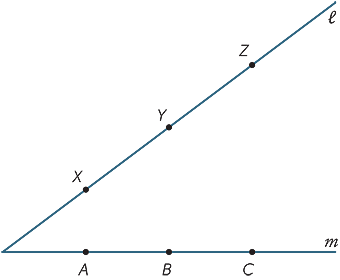
Faça uma grande cópia do diagrama abaixo. Os pontos X, Y, Z são pontos em que a linha  e A, B ,C são pontos em que a linha m. Junte-AY e XB chamar a sua intersecção R. Junte-BZ e YC e chamar a sua intersecção P. Junte-CX e ZA e chamar a sua intersecção P. o Que você observa sobre os pontos P, Q, R? (This result is called Pappus’ theorem, C. 340 AD.)
e A, B ,C são pontos em que a linha m. Junte-AY e XB chamar a sua intersecção R. Junte-BZ e YC e chamar a sua intersecção P. Junte-CX e ZA e chamar a sua intersecção P. o Que você observa sobre os pontos P, Q, R? (This result is called Pappus’ theorem, C. 340 AD.)
intervalos, raios e ângulos
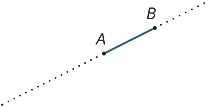 suponha que A e B são dois pontos em uma linha. O intervalo
suponha que A e B são dois pontos em uma linha. O intervalo
AB é a parte da linha entre A e B, incluindo os dois parâmetros.
Figura M1 8.o ponto A do diagrama divide a linha em duas partes chamadas raios. O raio AP é aquele que contém o ponto P (E o ponto A).
Ângulos
Diagrama M1. 9.no diagrama, a região sombreada entre os raios OA e OB é chamada de AOB angular ou BOA angular. O sinal de ângulo ![]() está escrito por isso escrevemos
está escrito por isso escrevemos ![]() AOB.
AOB.
Figura M1 10.a região sombreada no exterior é chamada de ângulo reflexo formado por OA e OB. Na maioria das vezes, a menos que especificemos o reflexo da palavra, todos os nossos ângulos se referem à área entre os raios e não fora deles.
o tamanho de um ângulo
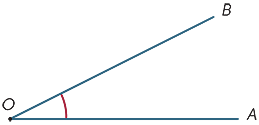 Imagine que o ray OB é rodado sobre o ponto O até que ele se encontra ao longo OA. A quantidade de rotação é chamada o tamanho do AOB ângulo. Podemos igualmente definir o tamanho do ângulo de reflexo.
Imagine que o ray OB é rodado sobre o ponto O até que ele se encontra ao longo OA. A quantidade de rotação é chamada o tamanho do AOB ângulo. Podemos igualmente definir o tamanho do ângulo de reflexo.
usaremos frequentemente pequenas letras gregas, α, β, γ,… para representar o tamanho de um ângulo.
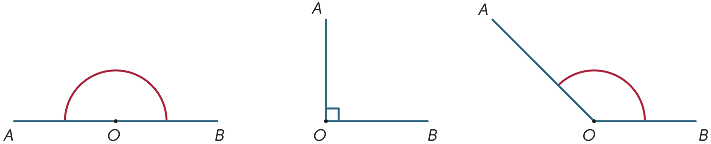
o tamanho do ângulo correspondente a uma revolução completa foi dividido (pelos babilônios) em 360 partes iguais, que chamamos de graus. (Eles provavelmente escolheram 360, uma vez que estava perto do número de dias em um ano. Assim, o tamanho de um ângulo reto é de 180° e o tamanho de um ângulo reto é de 90°. Outros ângulos podem ser medidos (aproximadamente) usando um transferidor.
|
|
||
| ângulo Reto | ângulo Direito |
ângulo Obtuso |
os Ângulos são classificados de acordo com seu tamanho. Dizemos que um ângulo com o tamanho α é aguda
(uma palavra que significa “afiado”) se 0° < α < 90°, α é obtuso (uma palavra que significa ‘rombo’) se
90° < α < 180° e α é reflexo de se 180° < α < 360°.
uma vez que o transferidor tem duas escalas, os alunos precisam de ter cuidado ao desenhar e
medir os ângulos. É um exercício que vale a pena usar um transferidor para desenhar alguns ângulos, tais como: 30°, 78°, 130°, 163°. Exercício 3
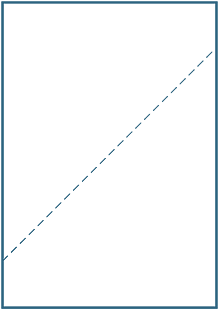 Fold an A4 sheet of paper matching up the (diagonal) opposite corners. Desenha uma linha ao longo do vinco que é formado e mede os ângulos entre o vinco e o lado.
Fold an A4 sheet of paper matching up the (diagonal) opposite corners. Desenha uma linha ao longo do vinco que é formado e mede os ângulos entre o vinco e o lado.
no exercício acima, os dois ângulos juntos formam uma linha reta e assim adicionar a 180°. Dois ângulos que se adicionam a 180° são chamados ângulos suplementares; assim, 45° e 135° são ângulos suplementares.
dois ângulos que se adicionam a 90° são chamados de Complementares; assim, 23° e 67° são
ângulos complementares.
ângulos num ponto
Diagrama M1. 14.dois ângulos em um ponto são ditos adjacentes se eles compartilham um raio comum. Assim, no diagrama, ![]() AOB e
AOB e ![]() BOC são adjacentes.
BOC são adjacentes.
ângulos adjacentes podem ser adicionados, de modo que no diagrama
α = β + γ. Quando duas linhas se intersectam, formam-se quatro ângulos no ponto de intersecção.
no diagrama, os ângulos marcados com ![]() AOX e
AOX e ![]() BOY são chamados verticalmente opostos.
BOY são chamados verticalmente opostos.
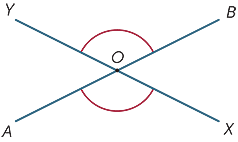 desde
desde
-
 AOX é o suplemento de
AOX é o suplemento de  BOX (ângulo recto).
BOX (ângulo recto). -
 BOY is also the supplement of
BOY is also the supplement of  BOX (straight angle),
BOX (straight angle),
podemos concluir que estes ângulos verticalmente opostos,
![]() AOX e
AOX e ![]() BOY são iguais. Assim, temos a nossa primeira declaração geométrica importante:
BOY são iguais. Assim, temos a nossa primeira declaração geométrica importante:
os ângulos verticalmente opostos são iguais.
um resultado em Geometria (e na matemática em geral) é muitas vezes chamado de teorema. Um teorema é uma afirmação importante que pode ser provada por dedução lógica. O argumento acima é uma prova do teorema; às vezes as provas são apresentadas formalmente após a afirmação do teorema.
 If two lines intersect so that all four angles are right-angles, then the lines are said to be perpendicular.
If two lines intersect so that all four angles are right-angles, then the lines are said to be perpendicular.
ângulos em argumentos geométricos de ponto
as seguintes razões podem ser usadas em argumentos geométricos:
- os ângulos adjacentes podem ser adicionados ou subtraídos.
- Angles in a revolution add to 360°.
- ângulos em uma linha reta adicionar a 180°.
- ângulos verticalmente opostos são iguais.
transversais e linhas paralelas
 a transversal é uma linha que atende duas outras linhas.
a transversal é uma linha que atende duas outras linhas.
os ângulos correspondentes
vários ângulos são formados pelo transversal. Nos diagramas abaixo, os dois ângulos marcados são chamados ângulos correspondentes.
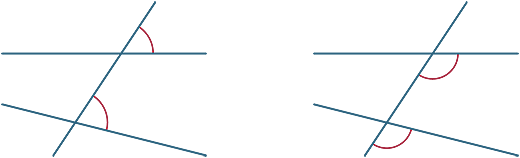
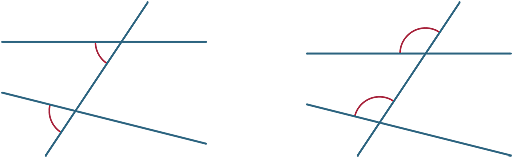
figura M1 21.agora vemos o que acontece quando as duas linhas cortadas pelo transversal são paralelas.
Inituitivamente, se o ângulo α fosse maior que β, então CD cruzaria AB para a esquerda de F E se fosse menor que β, cruzaria para a direita de F. assim, uma vez que as linhas não cruzam em tudo, α Não pode ser nem menos nem mais do que β e assim é igual a β.
alternativamente, imagine traduzir o ângulo QGD ao longo de GF até que G coincida com F. Uma vez que as linhas são paralelas, seria de esperar que o ângulo α coincidisse com o ângulo β. Esta observação leva-nos a conjecturar que: Os ângulos correspondentes formados a partir de linhas paralelas são iguais.
não podemos provar este resultado, embora tenhamos mostrado que é geometricamente plausível. Vamos aceitá-la como um axioma da geometria. Um axioma é uma afirmação que não podemos provar, mas que é intuitivamente razoável. Note que muitos dos fatos que já afirmamos, tais como: ângulos adjacentes podem ser adicionados, e dois pontos determinam uma linha, etc., são também axiomas, embora não os tenhamos declarado explicitamente desta forma.
ângulos alternados
em cada diagrama os dois ângulos marcados são chamados de Ângulos alternados (uma vez que eles estão em lados alternados do transversal).

 If the lines AB and CD are parallel, then the alternate angles are equal. Este resultado pode agora ser provado.
If the lines AB and CD are parallel, then the alternate angles are equal. Este resultado pode agora ser provado.
![]() DGQ = α (correspondentes ângulos, AB ||CD)
DGQ = α (correspondentes ângulos, AB ||CD)
![]() DGQ = β (verticalmente ângulos opostos em G)
DGQ = β (verticalmente ângulos opostos em G)
Portanto, α = β.
resumindo:
os ângulos alternados formados a partir de linhas paralelas são iguais.
ângulos Co-interiores
finalmente, em cada diagrama abaixo, os dois ângulos marcados são chamados ângulos Co-interiores e ficam do mesmo lado do transversal.

se as linhas AB e CD são paralelas, então é óbvio que os ângulos Co-interiores não são iguais, mas acontece que eles são suplementares, ou seja, sua soma é 180° .
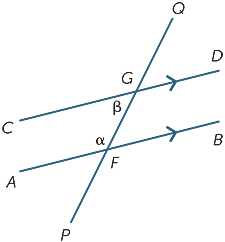 este é um resultado que também é fácil de provar:
este é um resultado que também é fácil de provar:
![]() BFG = β (ângulos alternativos, AB ||CD)
BFG = β (ângulos alternativos, AB ||CD)
α + β = 180° (ângulo reto em F)
Para resumir:
Co-interior ângulos formados a partir de linhas paralelas são complementares. Figura M1 24.pdfOs três resultados podem ser resumidos
pelo diagrama a seguir:
Exemplos Numéricos
Dado informações sobre os ângulos em um diagrama, podemos usar os resultados acima para encontrar o tamanho de outros ângulos no diagrama. Esta é uma habilidade simples, mas muito importante, muitas vezes referido informalmente como perseguição de ângulo. Na resolução de problemas, a sequência de passos nem sempre é única. Pode haver várias abordagens diferentes, mas igualmente válidas.
por exemplo, no diagrama seguinte, procuramos o tamanho do ângulo BAC.

![]() DCA = 102° (ângulos alternativos, AC|BD)
DCA = 102° (ângulos alternativos, AC|BD)
![]() BAC = 78° (co-ângulos interiores, AB||CD)
BAC = 78° (co-ângulos interiores, AB||CD)
Exercício 4
Usar uma alternatie sequência de passos para encontrar ![]() BAC.
BAC.
Exercício 5
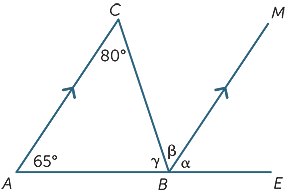 usando apenas propriedades de linhas paralelas, encontrar (com razões) os ângulos em falta no diagrama seguinte.
usando apenas propriedades de linhas paralelas, encontrar (com razões) os ângulos em falta no diagrama seguinte.
Exercício 6
Encontre o valor de α no diagrama seguinte.
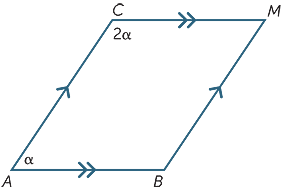
declarações convergentes
muitas declarações em matemática têm um inverso, no qual a implicação vai na direção oposta. Por exemplo, a declaração
‘todo número par termina em 0, 2, 4, 6 ou 8.’
tem converse
‘ Todo número que termina em 0, 2, 4, 6 ou 8 é par.”
esta afirmação específica e o seu inverso são ambos verdadeiros, mas este não é de modo algum sempre
o caso.
por exemplo, as duas afirmações seguintes são convergências entre si:
‘todo múltiplo de 4 é um número par.Cada número par é um múltiplo de 4.’
e aqui, a primeira afirmação é verdadeira, mas a segunda é falsa.
Exercício 7
Escrever:
um![]() um verdadeiro geométricas instrução cujo inverso também é verdadeiro,
um verdadeiro geométricas instrução cujo inverso também é verdadeiro,
b![]() false geométricas instrução cujo inverso é verdadeiro,
false geométricas instrução cujo inverso é verdadeiro,
c![]() um falso geométricas instrução cujo inverso também é falso.
um falso geométricas instrução cujo inverso também é falso.
The Converse Theorems for Parallel Lines
we have seen that corresponding angles formed from parallel lines are equal. Podemos escrever a declaração inversa da seguinte forma. Se as linhas são paralelas, então os ângulos correspondentes são iguais.
Converse: Se os ângulos correspondentes são iguais, então as linhas são paralelas.
a afirmação inversa também é verdadeira e é frequentemente usada para provar que duas linhas são paralelas. O mesmo se aplica aos ângulos alternados e co-interiores.
afirmação: se as linhas são paralelas, então os ângulos alternativos são iguais. Se os ângulos alternativos são iguais, então as linhas são paralelas.
afirmação: se as linhas são paralelas, então os ângulos co-interiores são suplementares.
Converse: Se os ângulos co-interiores são suplementares, então as linhas são paralelas.
assim, em cada diagrama, as linhas AB e CD são paralelas.

Exercício 8
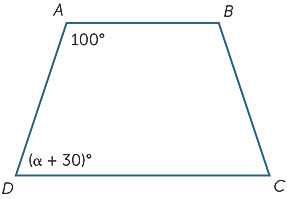 qual o valor de α fará AB paralelo ao CD?
qual o valor de α fará AB paralelo ao CD?
provas dos Três convertidos
Diagrama M1. 30.supomos que os ângulos correspondentes formados pelo transversal são iguais e mostramos que as linhas são paralelas.
no diagrama, supomos que
![]() ABC =
ABC = ![]() BEF.
BEF.
se BC e EF não são paralelos, então desenhe
BD paralelo à EF.
agora uma vez que BD e EF são paralelos ![]() ABD =
ABD = ![]() BEF e assim
BEF e assim ![]() ABC =
ABC = ![]() ABD o que é claramente impossível a menos que as linhas BC e BD sejam as mesmas. Assim, as linhas BC e EF são paralelas.
ABD o que é claramente impossível a menos que as linhas BC e BD sejam as mesmas. Assim, as linhas BC e EF são paralelas.
as outras provas seguem da mesma forma.
exercício 9
dar uma prova do segundo teorema inverso (ângulos alternativos).
soma dos ângulos de um triângulo
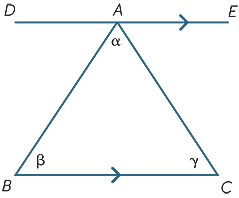 The results from the previous section can be used to deduce one of the most important facts in geometry-the angle sum of a triangle is 180° .
The results from the previous section can be used to deduce one of the most important facts in geometry-the angle sum of a triangle is 180° .
começamos com triângulo ABC com ângulos α, β, γ como mostrado. Trace a linha DAE paralela a BC. Em seguida,,
![]() DAB = β (ângulos alternativos, BC||DE)
DAB = β (ângulos alternativos, BC||DE)
![]() EAC = γ (ângulos alternativos, BC||DE)
EAC = γ (ângulos alternativos, BC||DE)
α+ β + γ = 180° (ângulo reto).
Thus, we have proved the theorem
The sum of the angles in a triangle is 180°. Um quadrilátero é uma figura plana delimitada por quatro lados.
exercício 10
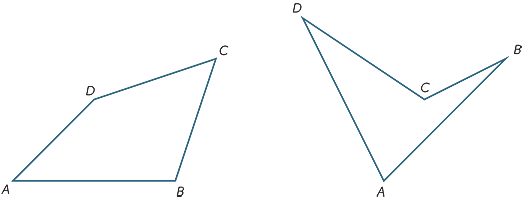
dividindo o ABCD quadrilateral em dois triângulos, encontre a soma dos ângulos.
Links para a frente
O material deste módulo começou a colocar geometria razoavelmente sistemática fundação de cuidadosamente definidos, objetos, axiomas que devem ser assumidos e teoremas que já provamos. Nesta base, podemos desenvolver um relato sistemático da geometria plana envolvendo:
- base no teorema de Pitágoras
- congruência e congruentes os triângulos
- semelhança e similares, triângulos
- isósceles e equilátero triângulos
- especial quadriláteros, incluindo quadrados, retângulos, paralelogramos, paralelogramos e trapezia
- a geometria dos círculos.
a geometria plana também será fundamental em muitas outras áreas dos anos 7-10 matemática:
- transformações
- geometria tridimensional
- áreas e volumes
- trigonometria
- coordenar a geometria
- os gráficos de círculos e parábolas.
as ideias de tangentes e áreas levam, por sua vez, ao cálculo nos anos 11-12.
História e o Aplicativo
História
O incrível construções das pirâmides e os enormes templos do Egito revelam que os Egípcios devem ter tido um trabalho muito bom conhecimento e compreensão das noções básicas de geometria, pelo menos, a nível prático. Por outro lado, não há provas de que tenham sistematizado esse conhecimento de forma formal. Isto foi deixado para os gregos antigos. Não temos conhecimento detalhado dessa sistematização, excepto no que se refere à alegação de que Tales(ca. 624 AC-ca. 546 A. C.) deu as primeiras “provas” de fatos geométricos que marcaram o início da geometria dedutiva. A Escola Pitagórica continuou este trabalho e Platão (428 A.C. -348 BC) é claramente baseado no trabalho de matemáticos anteriores, quando ele menciona fatos geométricos em seus escritos. O diálogo geométrico em sua obra o Meno, no qual Sócrates consegue que um menino escravo chegue a um teorema geométrico por uma série de deduções lógicas, vale a pena ler. Se as origens da geometria não são claras, o “produto final” não é. Euclides (323-283 A. C.), escrevendo em Alexandria, produziu uma obra notável, chamada Os elementos, que permaneceu o livro padrão em Geometria por mais de 2000 anos. Neste trabalho, Euclid define uma série de definições (como pontos e linhas), postulados e noções comuns. (Hoje em dia chamamos-lhes axiomas. A partir destes, ele logicamente desenvolveu, em uma ordem cuidadosamente escolhida, um grande número de teoremas que geralmente nos referimos como geometria euclidiana. Há uma série de outros resultados geométricos, como o teorema de Pappus, que foram descobertos após Euclides, mas estes não são geralmente cobertos na escola secundária. Um dos cinco postulados de Euclides não era tão obviamente verdadeiro quanto os outros pareciam ser. Uma versão dela, conhecida como axioma de Playfair, afirma que: Dada uma linha  e um ponto P, não em
e um ponto P, não em  , existe uma e somente uma linha paralela à linha
, existe uma e somente uma linha paralela à linha  passando por P. No século 19, um número de matemáticos a pergunta ‘o Que acontece se podemos negar esse postulado?”Isto é feito assumindo que ou não existe tal linha paralela, ou dizendo que há mais de uma tal linha. Isto levou ao desenvolvimento de geometrias não-euclidianas, uma das quais acabou por fornecer um dos bons modelos para o universo.
passando por P. No século 19, um número de matemáticos a pergunta ‘o Que acontece se podemos negar esse postulado?”Isto é feito assumindo que ou não existe tal linha paralela, ou dizendo que há mais de uma tal linha. Isto levou ao desenvolvimento de geometrias não-euclidianas, uma das quais acabou por fornecer um dos bons modelos para o universo.
aplicações
num sentido muito real, geometria e intuição geométrica formam os fundamentos de todos
Matemática − Geometria leva a geometria coordenada que leva ao cálculo e
todas as suas muitas aplicações − e por isso é crucial no currículo.
em um nível mais prático, Construtores, topógrafos, engenheiros e arquitetos têm sido usuários pesados de geometria e ideias geométricas por séculos. Mais recentemente, com o desenvolvimento de computadores, artistas gráficos e web designers juntaram-se a este grupo de pessoas que precisam e usam geometria em seu trabalho. Quando perguntado recentemente como a geometria é útil, Jim Kelly, um cientista aplicado disse :.. geometria é uma parte importante do design, desenho e modelagem de computador. Também é usado frequentemente em … física e outros cursos de ciências físicas como parte da compreensão dos efeitos de cargas sobre estruturas e pontos de equilíbrio(centros de gravidade) para sólidos compostos. Em química, a compreensão da geometria de uma molécula está relacionada à compreensão das propriedades das substâncias. Existem muitos mais exemplos. (from Ask a Scientist website.)
A History of Mathematics: Uma Introdução, 3ª Edição, Victor J. Katz, Addison-Wesley, (2008)
História da Matemática, D. E. Smith, Dover publications Nova York, (1958)
RESPOSTAS AOS EXERCÍCIOS
EXERCÍCIO 1
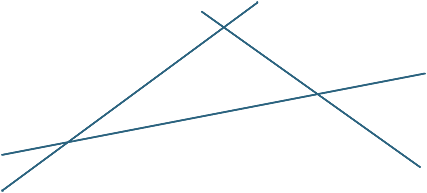
EXERCÍCIO 2
Os pontos são colineares
EXERCÍCIO 3
60°
EXERCÍCIO 4
![]() DBA = 102° (ângulos correspondentes, AB||CD)
DBA = 102° (ângulos correspondentes, AB||CD)
![]() BAC = 78° (co-ângulos interiores, AC||BD)
BAC = 78° (co-ângulos interiores, AC||BD)
EXERCÍCIO 5
α = 65°![]() (correspondentes ângulos, AC||BM)
(correspondentes ângulos, AC||BM)
β = 80°![]() (ângulos alternativos, AC||BM)
(ângulos alternativos, AC||BM)
γ + β = 115°![]() (co-ângulos interiores, AC||BM)
(co-ângulos interiores, AC||BM)
Portanto, γ = 35°
(Esta é a estrutura de uma prova do resultado a que o ângulo de soma de um triângulo é 180°)
exercício 6
α = 60°
exercício 7
a ![]() quadrilátero com cada um dos seus ângulos interiores, um ângulo recto é um rectângulo.
quadrilátero com cada um dos seus ângulos interiores, um ângulo recto é um rectângulo.
inverso: cada ângulo interior de um retângulo é um ângulo reto.
b![]() Um retângulo é um quadrado
Um retângulo é um quadrado
Conversar: Um quadrado é um retângulo
c![]() O ângulo soma dos ângulos interiores de um triângulo é de 200°
O ângulo soma dos ângulos interiores de um triângulo é de 200°
Conversar: Um polígono cuja soma dos ângulo interior é de 200° é um triângulo. Exercício 8
α = 50°
exercício 9
referimo-nos ao mesmo diagrama.
colocar um ponto H na linha EF à esquerda de E.
![]() CBE =
CBE = ![]() BEH
BEH
se BC e EF não forem paralelos então desenhar BD paralelo à EF.
uma vez que BD e EF são paralelos, ![]() EBD=
EBD= ![]() BEH, o que é claramente impossível a menos que as linhas BC e BD sejam as mesmas.
BEH, o que é claramente impossível a menos que as linhas BC e BD sejam as mesmas.
portanto, as linhas BC e EF são paralelas.Exercício 10
360°
o projeto Improving Mathematics Education in Schools (TIMES) 2009-2011 foi financiado pelo Departamento de Educação, Emprego e Relações laborais do Governo Australiano.
os pontos de vista aqui expressos são os do autor e não representam necessariamente os pontos de vista do Departamento de Educação, Emprego e Relações laborais do Governo Australiano.
© the University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). Este trabalho é licenciado sob a licença Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()