hoje será uma breve introdução às estatísticas circulares (por vezes referidas como estatísticas direcionais). Estatísticas circulares é uma subdivisão interessante de estatísticas envolvendo observações tomadas como vetores em torno de um círculo unitário. Como exemplo, imagine medir o tempo de nascimento em um hospital durante um ciclo de 24 horas, ou a dispersão direcional de um grupo de animais migratórios. Este tipo de dados está envolvido em uma variedade de campos, tais como ecologia, climatologia e bioquímica. A natureza das observações de medição em torno de um círculo unitário requer uma abordagem diferente para o teste de hipóteses. Distribuições precisam ser “enroladas” em torno do círculo para serem de uso, e estimadores convencionais, como a média da amostra ou variância da amostra não possuem água.
neste post, realizaremos o teste de espaçamento de Rao para avaliar a uniformidade de um conjunto de dados circular. Este é um procedimento básico e deve ser considerado como uma introdução ao tratamento de dados circulares.
iniciando
vamos realizar um teste de hipótese em tartarugas, um pequeno conjunto de dados que consiste nos ângulos de chegada de 10 tartarugas marinhas verdes à sua ilha de nidificação. Nosso objetivo é determinar onde os ângulos de chegada mostram sinais de direcionalidade ou são mais indicativos de uma dispersão aleatória.
em primeiro lugar, instale o pacote circular e anexe o conjunto de dados das tartarugas.
install.packages("circular")require(circular)attach(turtles)
plotando os dados
o pacote circular contém a sua própria função plotora, plot.circular. Vamos observar os ângulos de chegada das tartarugas.
plot.circular(arrival)
aqui está a parcela: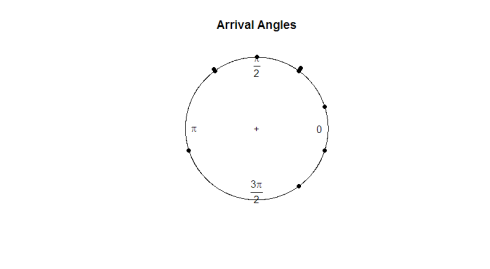
tendo em conta o ensaio ocular, as observações parecem ser uniformes à volta do círculo. Se quisermos fazer um teste de hipótese para determinar se os dados são realmente uniformes, precisaremos desenvolver uma estatística de teste que funcione com dados angulares.
o que é um bom parâmetro para nós utilizar? Tomar a amostra significa não nos diz muito sobre a direção dos dados (180 graus não é uma média útil de 2 graus e 358 graus). Na seguinte parcela, observe como a média da amostra não serve para representar a forma ou a propagação dos nossos dados.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
aqui está a parcela: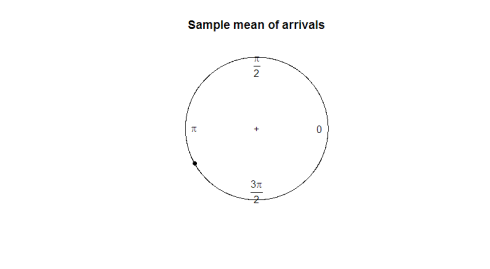
em vez disso, vamos usar um método que determina a direcionalidade medindo o espaço médio entre observações. Este teste é chamado de teste de espaçamento de Rao.
Rao’s Spacing Test
Rao’s Spacing Test was developed to assess the uniformity of circular data. Ele usa o espaço entre observações para determinar se os dados mostram direcionalidade significativa. Se os dados forem uniformes, as observações devem tender a ser uniformemente espaçadas.
aqui está a estatística de ensaio \(U\) para o ensaio de espaçamento de Rao: $$U = 1/2\sum\limits_{i=1}^n |T_{i} – λ| $$ onde \(λ = 360/n, T_{i} = f_{i+1}-f_{i}\) e \(T_{n} = (360-f_{n})+f_{1}\)
Basicamente, o teste estatístico agrega os desvios entre pontos consecutivos, cada um ponderado pelo número total de observações no conjunto de dados.
usaremos a função rao.spacing.test() para executar este teste de hipóteses. Nossa hipótese nula diz que os dados são de uma distribuição uniforme, enquanto os Estados Alternativos os dados mostram sinais de direcionalidade. Vamos fazer o teste.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
com uma estatística de ensaio de 127 inferior ao valor crítico de 161, os dados não se inclinam significativamente em qualquer direcção. Não podemos rejeitar a hipótese de que as tartarugas chegadas são de uma distribuição uniforme.
Conclusion
Rao’s spacing test determined the data to show no signs of directional trends. Não podemos rejeitar a hipótese nula de uniformidade e assumiremos uniformidade em relação à direção de chegada. Enquanto este post foi um tutorial relativamente básico, muitas pessoas na comunidade de ciência dos dados não trabalharam com dados circulares antes. É um interessante subtópico mergulhar em, bem como um campo jovem de estatísticas que ainda está evoluindo.
final remarks
I would like to extend credit to S. Rao Jammalamadaka PhD, of the University of California, Santa Barbara, and his textbook “Topics in Circular Statistics” for sparking my interest in the field of circular statistics.