4.2 Estimar os Coeficientes do Modelo de Regressão Linear

Na prática, a interseção $\beta_0$ e inclinação de $\beta_1$ da população linha de regressão são desconhecidos. Portanto, devemos empregar dados para estimar ambos os parâmetros desconhecidos. A seguir, um exemplo do mundo real será usado para demonstrar como isso é alcançado. Queremos relacionar os resultados dos testes com os índices de alunos-professores medidos nas escolas da Califórnia. A pontuação de teste é a média Distrital de leitura e matemática para alunos do quinto ano. Mais uma vez, o tamanho da classe é medido como o número de alunos divididos pelo número de professores (a relação aluno-professor). Quanto aos dados, o conjunto de dados da Escola da Califórnia (CASchools) vem com um pacote R chamado AER, um acrônimo para Econometria aplicada com R (Kleiber e Zeileis 2020). Depois de instalar o pacote com install.pacotes (“AER”) e anexá-lo com biblioteca(AER) o conjunto de dados pode ser carregado usando os dados da função ().

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

uma vez que um pacote foi instalado, ele está disponível para uso em outras ocasiões quando invocado com o library() — não há necessidade de executar install.pacotes () novamente!É interessante saber com que tipo de objeto estamos lidando.o class () devolve a classe de um objecto. Dependendo da classe de um objeto, algumas funções (por exemplo, plot() e summary()) comportam-se de forma diferente.

vamos verificar a classe dos casquilhos de objectos.

class(CASchools)#> "data.frame"

acontece que o CASchools é de dados de classe.frame que é um formato conveniente para trabalhar, especialmente para a realização de análise de regressão.Com a ajuda do head() obtemos uma Primeira Visão geral dos nossos dados. Esta função mostra apenas as primeiras 6 linhas do conjunto de dados que previne uma saída de consola superlotada.

Carregue em ctrl + L para limpar a consola. Este comando apaga qualquer código que tenha sido digitado e executado por si ou impresso na consola por funções R. A boa notícia é que tudo o resto fica intacto. Você não perde variáveis definidas, etc. nem a história do Código. Ainda é possível recordar os comandos R previamente executados usando as teclas para cima e para baixo. Se estiver a trabalhar no RStudio, carregue em ctrl + Up no seu teclado (CMD + Up num Mac) para rever uma lista de comandos introduzidos anteriormente.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

descobrimos que o conjunto de dados consiste de muitas variáveis e que a maioria delas são numéricas.

a propósito: uma alternativa para classe() e cabeça() é str () que é deduzido de “estrutura” e dá uma visão abrangente do objeto. Tenta!As duas variáveis em que estamos interessados (i.e. não estão incluídos os resultados médios dos testes e a relação aluno-professor. No entanto, é possível calcular ambos a partir dos dados fornecidos. Para obter os rácios Aluno-Professor, nós simplesmente dividimos o número de alunos pelo número de professores. A pontuação média do teste é a média aritmética da pontuação do teste para leitura e a pontuação do teste de matemática. O próximo bloco de código mostra como as duas variáveis podem ser construídas como vetores e como elas são anexadas a CASchools.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

se corrêssemos head (CASchools) novamente encontraríamos as duas variáveis de interesse como colunas adicionais chamadas STR e score(veja isto!).

a tabela 4.1 do manual resume a distribuição das pontuações dos testes e rácios Aluno-Professor. Existem várias funções que podem ser usadas para produzir resultados semelhantes, como por exemplo:,

média() (calcula a média aritmética dos números fornecidos),
sd() (calcula o desvio padrão da amostra),
gráfico quantil() (retorna um vetor de exemplo de quantis para os dados).

o próximo bloco de código mostra como conseguir isso. Primeiro, nós computamos estatísticas sumárias sobre as colunas STR e pontuação de CASchools. A fim de obter uma boa saída nós coletamos as medidas em um dado.frame named DistributionSummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

quanto aos dados da amostra, usamos plot(). Isto permite-nos detectar características dos nossos dados, tais como anómalos que são mais difíceis de descobrir ao olhar para meros números. Desta vez adicionamos alguns argumentos adicionais ao chamado de plot().

o primeiro argumento em nosso call of plot (), score ~ STR, é novamente uma fórmula que afirma variáveis no eixo y – e x -. Entretanto, desta vez as duas variáveis não são salvas em vetores separados, mas são colunas de CASchools. Por conseguinte, o R não os encontraria sem que os dados relativos aos argumentos fossem correctamente especificados. os dados devem estar de acordo com o nome dos dados.quadro a que as variáveis pertencem, neste caso, os CASchools. Outros argumentos são usados para alterar a aparência do gráfico: enquanto o main adiciona um título, o xlab e o ylab adicionam legendas personalizadas a ambos os eixos.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")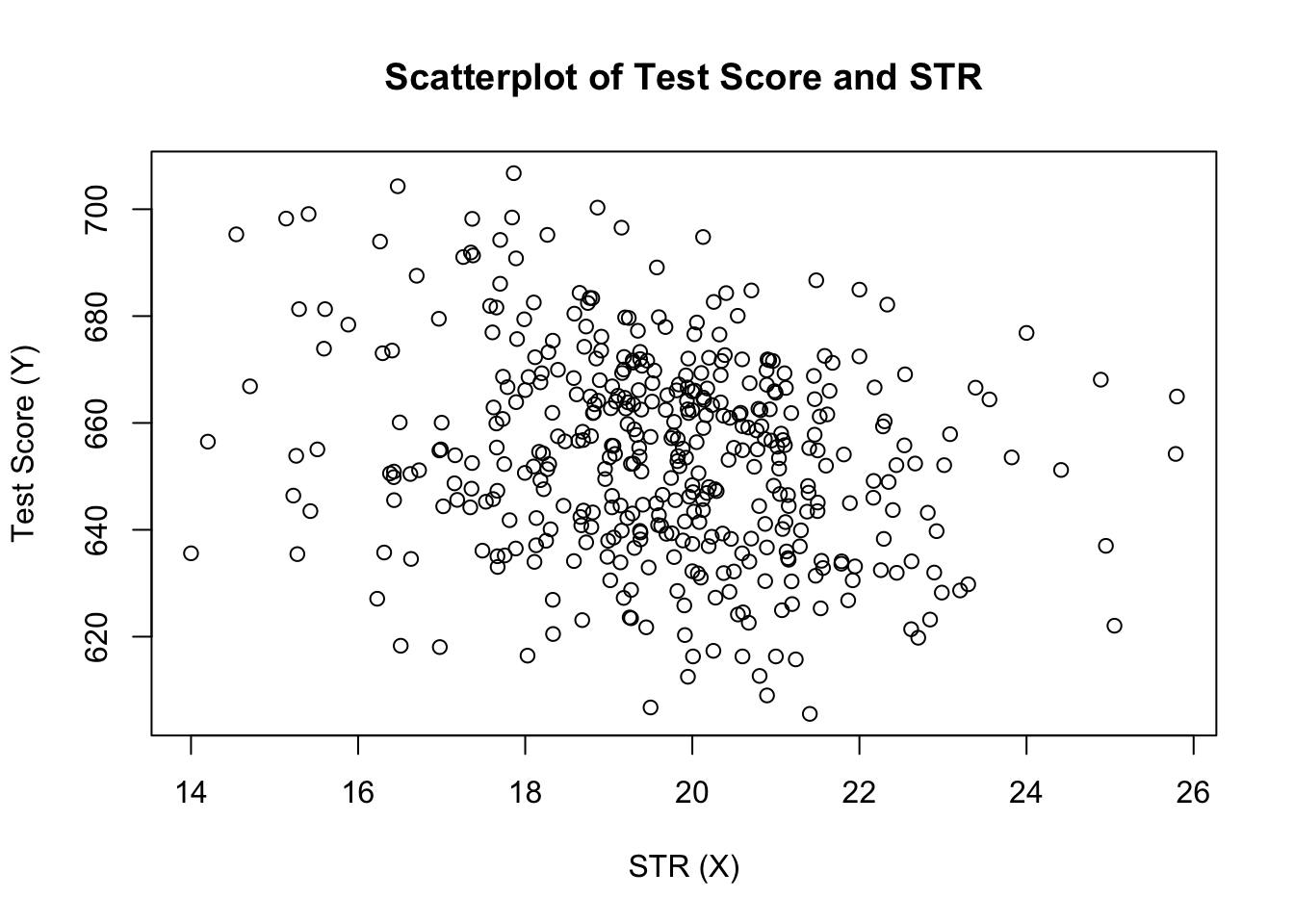

o gráfico (figura 4.2 do livro) mostra o resumo de todas as observações sobre a relação aluno-professor e a pontuação de teste. Vemos que os pontos estão fortemente dispersos, e que as variáveis estão negativamente correlacionadas. Ou seja, esperamos observar resultados de testes mais baixos em classes maiores.

a função cor () (Ver ?cor para mais informações) pode ser usado para calcular a correlação entre dois vetores numéricos.

cor(CASchools$STR, CASchools$score)#> -0.2263627

como o scatterplot já sugere, a correlação é negativa, mas bastante fraca.

a tarefa que estamos enfrentando agora é encontrar uma linha que se encaixe melhor nos dados. É claro que poderíamos simplesmente ficar com a inspeção gráfica e análise de correlação e, em seguida, selecionar a melhor linha de montagem por eyeballing. No entanto, isso seria bastante subjetivo: diferentes observadores desenhariam diferentes linhas de regressão. Por isso, estamos interessados em técnicas menos arbitrárias. Tal técnica é dada pela estimativa dos mínimos quadrados ordinários (OLS).

o estimador dos mínimos quadrados ordinários

o estimador OLS escolhe os coeficientes de regressão tal que a linha de regressão estimada seja o mais “próxima” possível dos pontos de dados observados. Aqui, a proximidade é medida pela soma dos erros ao quadrado cometidos na previsão $Y$ dado $X$. Seja $b_0$ e $b_1$ alguns estimadores de $\beta_0$ e $\beta_1$. Em seguida, a soma dos erros de estimativa ao quadrado pode ser expressa como

o estimador OLS no modelo de regressão simples é o par de estimadores para interceptação e declive que minimiza a expressão acima. O cálculo dos estimadores OLS para ambos os parâmetros é apresentado no Apêndice 4.1 do livro. Os resultados são resumidos no conceito-chave 4.2.

O Estimador de mínimos quadrados ordinários, os Valores Previstos, e Residuais

Os estimadores OLS da encosta $\beta_1$ e a interseção $\beta_0$ o simples modelo de regressão linear são\O OLS valores previstos $\widehat{Y}_i$ e resíduos de $\hat{u}_i$ são\

A estimativa de interceptar $\hat{\beta}_0$, a inclinação parâmetro $\hat{\beta}_1$ e os resíduos $\left(\hat{u}_i\right)$ são calculadas a partir de uma amostra de $n$ observações de $X_i$ e $Y_i$, $i$, $…$, $n$. Estas são as estimativas da interceptação da população desconhecida $\esquerda (\beta_0 \direita)$, do declive $\esquerda(\beta_1\direita)$ e do termo de erro $((u_i)$.

as fórmulas apresentadas acima podem não ser muito intuitivas à primeira vista. A aplicação interativa que se segue pretende ajudá-lo a compreender a mecânica dos OLS. Você pode adicionar observações clicando no sistema de coordenadas onde os dados são representados por pontos. Uma vez que duas ou mais observações estão disponíveis, A aplicação calcula uma linha de regressão usando OLS e algumas estatísticas que são exibidas no painel direito. Os resultados são atualizados à medida que você adiciona mais observações ao painel esquerdo. Um duplo clique reinicializa a aplicação, ou seja, todos os dados são removidos.

Existem muitas formas possíveis de computação $\hat{\beta}_0$ e $\hat{\beta}_1$ em R. Por exemplo, poderíamos implementar as fórmulas apresentadas no Conceito-Chave 4.2 com dois de R funções mais básicas: média() e sum(). Antes de o fazer, anexamos o conjunto de dados do CASchools.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

invocando adido (CASchools) permite-nos adressar uma variável contida em CASchools pelo seu nome: não é mais necessário usar o operador $ em conjunto com o conjunto de dados: R pode avaliar o nome da variável diretamente.

R usa o objeto no ambiente do Usuário se este objeto compartilha o nome da variável contida em uma base de dados anexada. No entanto, é uma melhor prática usar sempre nomes distintivos, a fim de evitar tais ambivalências (aparentemente)!

note que nós adicionamos variáveis contidas no conjunto de dados anexado CASchools diretamente para o resto deste capítulo!

é claro que existem ainda mais formas manuais de executar estas tarefas. Com OLS sendo uma das técnicas de estimação mais amplamente utilizadas, R já contém uma função incorporada chamada lm () (modelo linear) que pode ser usada para realizar a análise de regressão.

O primeiro argumento da função a ser especificado é, semelhante ao plot(), a fórmula de regressão com a sintaxe básica y ~ x, onde y é a variável dependente e x a variável explicativa. Os dados dos argumentos determinam o conjunto de dados a utilizar na regressão. Agora revisitamos o exemplo do livro onde se analisa a relação entre as pontuações dos testes e os tamanhos das classes. O seguinte código utiliza lm() para replicar os resultados apresentados na figura 4.3 do livro.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

vamos adicionar a linha de regressão estimada ao enredo. Desta vez, também aumentamos as gamas de ambos os eixos, definindo os argumentos xlim e ylim.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)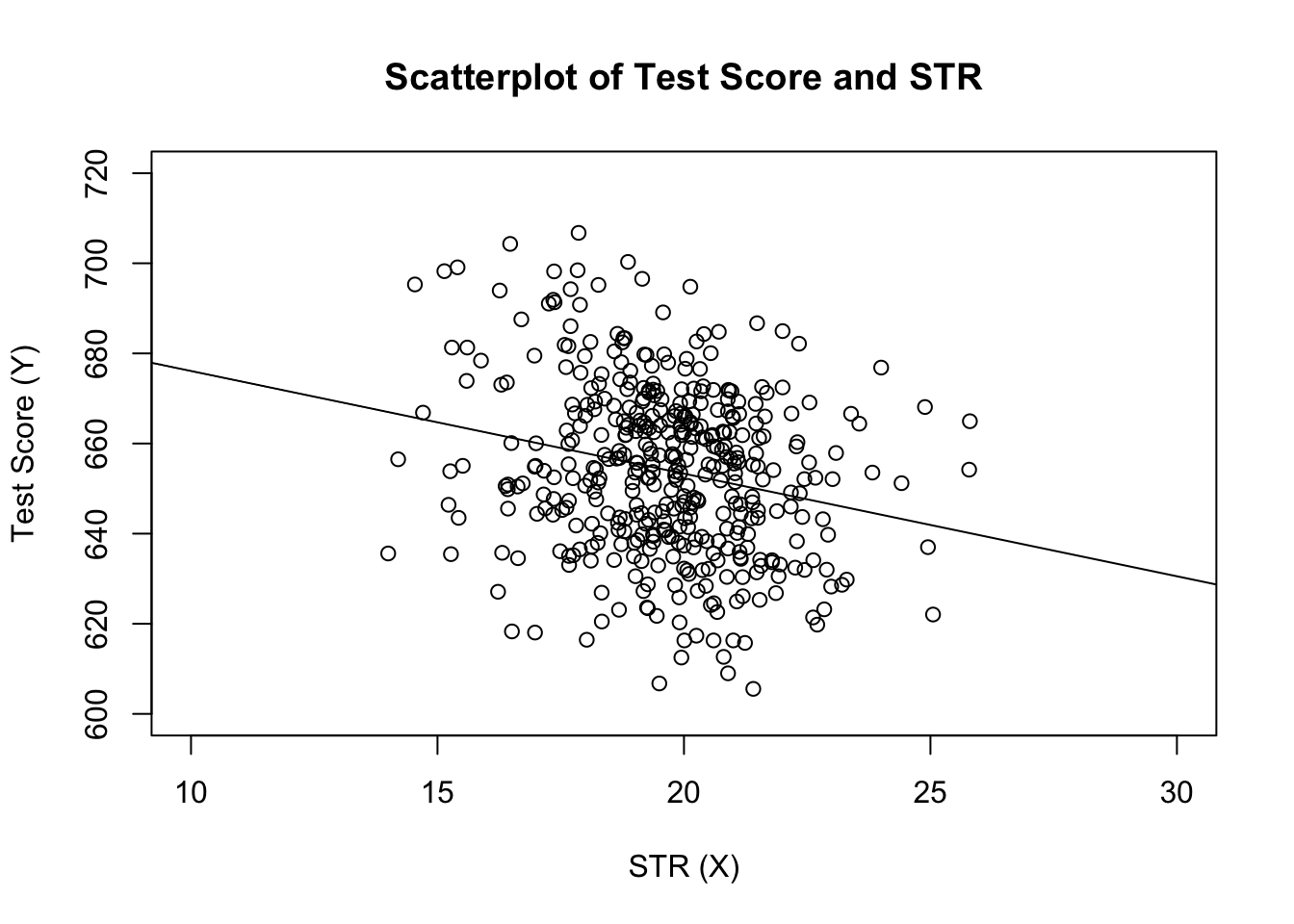

reparou que desta vez não passamos os parâmetros de intercepção e inclinação para abline? Se você chamar abline () em um objeto da classe lm que só contém um único regressor, R Desenha a linha de regressão automaticamente!