Avaliação | Biopsychology | Comparativos |Cognitiva | Desenvolvimento | Language | diferenças Individuais |Personalidade | Filosofia | Sociais |
Métodos | Estatísticas |Clínica | Educacional | Industrial |Profissional itens Mundo |psicologia |
Estatísticas:Método científico · métodos de Pesquisa · Experimental · projeto de Graduação cursos de estatística · testes Estatísticos · Jogo · teoria da Decisão teoria
Análise de clusters ou clustering é uma técnica comum para análise de dados estatísticos, que é usada em muitos campos, incluindo aprendizagem de máquinas, mineração de dados, reconhecimento de padrões, análise de imagens e bioinformática. O cluster é a classificação de objetos semelhantes em diferentes grupos, ou, mais precisamente, o particionamento de um conjunto de dados em subconjuntos (clusters), de modo que os dados em cada subconjunto (idealmente) compartilhar algumas traço comum – muitas vezes de proximidade de acordo com alguns definido medida de distância.
além do termo agrupamento de dados (ou apenas agrupamento), há uma série de termos com significados semelhantes, incluindo análise de clusters, classificação automática, taxonomia numérica, botryologia e análise tipológica.
- tipos de clustering
- clustering hierárquico
- medida de distância
- criação de aglomerados
- clustering particional
- k-means and derivatives
- K-means clustering
- QT Clust algorithm
- Fuzzy c-means clustering
- critério do cotovelo
- Spectral clustering
- Applications
- Biology
- Marketing research
- outras aplicações
- comparações entre aglomerações de dados
- Veja também:
- Bibliografia
- implementações de Software
- Grátis
tipos de clustering
algoritmos de clusterização de dados podem ser hierárquicos ou parciais. Algoritmos hierárquicos encontram clusters sucessivos usando clusters previamente estabelecidos, enquanto algoritmos particionais determinam todos os clusters de uma vez. Algoritmos hierárquicos podem ser aglomerados (bottom-up) ou divisivos (top-down). Algoritmos aglomerativos começam com cada elemento como um conjunto separado e fundem-nos em conjuntos sucessivamente maiores. Algoritmos divisivos começam com todo o conjunto e avançam para dividi-lo em conjuntos sucessivamente menores.
clustering hierárquico
medida de distância
um passo-chave numa clusterização hierárquica é Seleccionar uma medida de distância. Uma medida simples é a distância de manhattan, igual à soma das distâncias absolutas para cada variável. O nome vem do fato de que em um caso de duas variáveis, as variáveis podem ser plotadas em uma grade que pode ser comparada às ruas da cidade, e a distância entre dois pontos é o número de blocos que uma pessoa caminharia.
uma medida mais comum é a distância Euclidiana, calculada encontrando o quadrado da distância entre cada variável, somando os quadrados, e encontrando a raiz quadrada dessa soma. No caso de duas variáveis, a distância é análoga a encontrar o comprimento da hipotenusa em um triângulo; isto é, é a distância “como o corvo voa.”A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.
criação de aglomerados
dada uma medida de distância, os elementos podem ser combinados. Hierarchical clustering builds (agglomerative), or breaks up (divisive), a hierarchy of clusters. A representação tradicional desta hierarquia é uma estrutura de dados de árvore (chamada de dendrograma), com elementos individuais em uma extremidade e um único conjunto com cada elemento na outra. Algoritmos aglomerativos começam no topo da árvore, enquanto algoritmos divisivos começam no fundo. (Na figura, as setas indicam um agrupamento aglomerativo.)
cortar a árvore a uma determinada altura dará um agrupamento a uma precisão selecionada. No exemplo seguinte, cortar após a segunda linha irá produzir clusters {a} {b c} {d E} {f}. Cortar após a terceira linha irá produzir clusters {a} {b c} {d E f}, Que é um agrupamento mais grosseiro, com um menor número de clusters maiores.Por exemplo, suponha que estes dados devem ser agrupados. Onde a distância euclidiana é a métrica da distância.
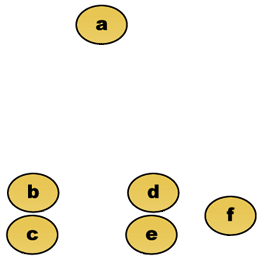
dados Brutos
hierárquica de cluster dendrograma seria como tal:
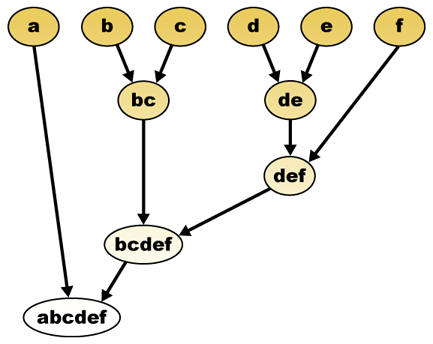
representação Tradicional
Este método cria a hierarquia dos elementos individuais por fusão progressiva de clusters. Mais uma vez, temos seis elementos {A} {b} {c} {d} {E} E {f}. O primeiro passo é determinar quais elementos se fundem em um conjunto. Normalmente, queremos tomar os dois elementos mais próximos, por isso temos de definir uma distância 
suponha que fundimos os dois elementos mais próximos b E c, agora temos os seguintes aglomerados {A}, {b, C}, {d}, {E} E {f}, e queremos fundi-los ainda mais. Mas para fazer isso, precisamos tomar a distância entre {a} e {b C}, e, portanto, definir a distância entre dois aglomerados. Normalmente, a distância entre dois clusters 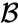
- A distância máxima entre os elementos de cada cluster (também chamado de complete linkage clustering):
- A distância mínima entre os elementos de cada cluster (também chamado de single linkage clustering):
- A distância média entre os elementos de cada cluster (também chamado de média linkage clustering):
- A soma de todos os intra-cluster de variância
- O aumento do desvio para o cluster está sendo mesclado (Ala critério)
- A probabilidade de que o candidato clusters de spawn da mesma função de distribuição (V-ligação)
Cada aglomeração ocorre uma maior distância entre os clusters do que o anterior aglomeração, e pode decidir parar de cluster ou quando os clusters estão demasiado distantes para serem fundidos (critério da distância) ou quando existe um número suficientemente pequeno de agregados (critério do número).
clustering particional
k-means and derivatives
K-means clustering
The K-means algorithm assigns each point to the cluster whose center (also called centroid) is nearest. O centro é a média de todos os pontos do aglomerado — ou seja, suas coordenadas são a média aritmética para cada dimensão separadamente sobre todos os pontos do aglomerado.
exemplo: O conjunto de dados tem três dimensões e o conjunto tem dois pontos: X = (x1, x2, x3) e Y = (y1, y2, y3). Então o centroid Z torna-se Z = (z1, z2, z3), onde z1 = (x1 + y1)/2 e z2 = (x2 + y2)/2 e z3 = (x3 + y3)/2.
o algoritmo é aproximadamente (J. MacQueen, 1967):
- gerar aleatoriamente aglomerados k e determinar os centros de aglomerado, ou gerar diretamente pontos de semente k como Centros de aglomerado.
- atribuir cada ponto ao centro de aglomerado mais próximo.
- Recompute the new cluster centers.
- repetir até que algum critério de convergência seja cumprido (geralmente que a atribuição não mudou).
as principais vantagens deste algoritmo são a sua simplicidade e velocidade que lhe permite executar em grandes conjuntos de dados. Sua desvantagem é que não produz o mesmo resultado em cada execução, uma vez que os clusters resultantes dependem das atribuições aleatórias iniciais. Maximiza a variância inter-cluster (ou minimiza a variância intra-cluster), mas não garante que o resultado tenha um mínimo global de variância.
QT Clust algorithm
QT (Quality Threshold) Clustering (Heyer et al, 1999) é um método alternativo de particionamento de dados, inventado para agrupamento de genes. Ele requer mais poder computacional do que k-means, mas não requer especificar o número de clusters a priori, e sempre retorna o mesmo resultado quando executado várias vezes.
o algoritmo é:
- o usuário escolhe um diâmetro máximo para aglomerados.
- construir um aglomerado candidato para cada ponto, incluindo o ponto mais próximo, o próximo mais próximo, e assim por diante, até que o diâmetro do aglomerado ultrapasse o limiar.
- salvar o cluster candidato com a maioria dos pontos como o primeiro cluster verdadeiro, e remover todos os pontos no cluster de consideração adicional.
- recursiva com o conjunto reduzido de pontos.
a distância entre um ponto e um grupo de pontos é calculada usando uma ligação completa, i.e. como a distância máxima entre o ponto e qualquer membro do Grupo (ver a seção “aglomerativa de agrupamento hierárquico” sobre a distância entre clusters).
Fuzzy c-means clustering
In fuzzy clustering, each point has a degree of belonging to clusters, as in fuzzy logic, rather than belonging completely to just one cluster. Assim, os pontos na borda de um aglomerado, podem estar no aglomerado em um grau menor do que os pontos no centro do aglomerado. Para cada ponto x temos um coeficiente que dá o grau de estar no aglomerado kth 

Com o fuzzy c-means, o centróide de um cluster é a média de todos os pontos, ponderada em função do seu grau de pertença ao cluster:
O grau de pertença está relacionado com o inverso da distância para o cluster
em seguida, os coeficientes são normalizados e fuzzyfied real de um parâmetro 
para m igual a 2, isto é equivalente a normalizar o coeficiente linearmente para fazer a sua soma 1. Quando m está perto de 1, Então o centro de aglomeração mais próximo do ponto é dado muito mais peso do que os outros, e o algoritmo é semelhante ao k-means.
o algoritmo fuzzy c-means é muito semelhante ao algoritmo k-means:
- escolha um número de grupos.
- atribuir aleatoriamente a cada ponto coeficientes para estar nos aglomerados.
- repetir até que o algoritmo tenha convergido (isto é, a mudança dos coeficientes entre duas iterações não é mais do que
, o limiar de sensibilidade dado) :
- Compute the centroid for each cluster, using the formula above.
- para cada ponto, calcule seus coeficientes de estar nos aglomerados, usando a fórmula acima.
o algoritmo minimiza a variância intra-cluster também, mas tem os mesmos problemas que K-means, o mínimo é um mínimo local, e os resultados dependem da escolha inicial de pesos.
critério do cotovelo
o critério do cotovelo é uma regra de polegar comum para determinar o número de aglomerados deve ser escolhido, por exemplo para K-means e aglomeração hierárquica.
o critério do cotovelo diz que você deve escolher um número de aglomerados para que a adição de outro aglomerado não adicione informação suficiente. Mais precisamente, se você gráfico a porcentagem de variância explicada pelos aglomerados contra o número de aglomerados, os primeiros aglomerados irão adicionar muita informação (explicar muita variância), mas em algum ponto o ganho marginal vai cair, dando um ângulo no grafo (o cotovelo).
no gráfico seguinte, o cotovelo é indicado pelo círculo vermelho. O número de agregados escolhidos deve, por conseguinte, ser de 4.
Spectral clustering
Dado um conjunto de pontos de dados, a matriz de similaridade pode ser definida como uma matriz 


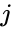
uma dessas técnicas é o algoritmo Shi-Malik, comumente usado para segmentação de imagem. Ele partições pontos em dois conjuntos 

de 
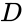
Este particionamento pode ser feito de várias maneiras, como, por exemplo, tendo a mediana 



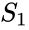
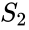
relacionado algoritmo é o Meila-Shi algoritmo, o que leva os autovetores correspondentes aos k maiores autovalores da matriz 
Applications
Biology
In biology clustering has many applications in the fields of computational biology and bioinformatics, two of which are:
- na transcriptomia, a clusterização é usada para construir grupos de genes com padrões de expressão relacionados. Muitas vezes, esses grupos contêm proteínas funcionalmente relacionadas, tais como enzimas para uma via específica, ou genes que são co-regulados. Experimentos de alta capacidade usando tags de sequência expressa (ESTs) ou microarray de DNA podem ser uma ferramenta poderosa para a anotação do genoma, um aspecto geral da genômica.
- em análise de sequência, a agregação é usada para agrupar sequências homólogas em famílias de genes. Este é um conceito muito importante na bioinformática, e biologia evolutiva em geral. See evolution by gene duplication.
Marketing research
Cluster analysis is widely used in market research when working with multivariate data from surveys and test panels. Os investigadores do mercado utilizam a análise de clusters para dividir a população em geral dos consumidores em segmentos de mercado e para compreender melhor as relações entre diferentes grupos de consumidores/potenciais clientes.
- segmentação do mercado e determinação dos mercados alvo
- posicionamento dos produtos
- desenvolvimento de novos produtos
- selecção dos mercados de ensaio (ver : técnicas experimentais)
outras aplicações
análise da rede Social: no estudo das redes sociais, o agrupamento pode ser usado para reconhecer comunidades dentro de grandes grupos de pessoas.
segmentação da imagem: Clustering pode ser usado para dividir uma imagem digital em regiões distintas para detecção de fronteiras ou reconhecimento de objetos.
mineração de Dados: Muitas aplicações de mineração de dados envolvem particionamento de itens de dados em subconjuntos relacionados; as aplicações de marketing discutidas acima representam alguns exemplos. Outra aplicação comum é a divisão de documentos, como páginas da World Wide Web, em gêneros.
comparações entre aglomerações de dados
tem havido várias sugestões para uma medida de semelhança entre duas aglomerações. Tal medida pode ser usada para comparar quão bem diferentes algoritmos de clustering de dados funcionam em um conjunto de dados. Muitas dessas medidas são derivadas da matriz de correspondência (também conhecida como matriz de confusão), por exemplo, a medida Rand e as medidas Fowlkes-Mallows Bk.
- Jain, Murty and Flynn: Data Clustering: A Review, ACM Comp. Surv., 1999. Disponivel.
- para outra apresentação de hierárquicos, K-means e fuzzy c-means, ver esta introdução ao agrupamento. Também tem uma explicação sobre a mistura de Gaussianos.
- David Dowe, Mixture Modelling page-other clustering and mixture model links.
- a tutorial on clustering
- The on-line textbook: Information Theory, inferência, and Learning Algorithms, by David J. C. MacKay includes chapters on k-means clustering, soft k-means clustering, and derivations including the E-M algorithm and the variational view of the E-M algorithm.
Veja também:
- k-means
- rede neural Artificial (ANN)
- Self-organizing map
- Expectativa de Maximização (EM)
Bibliografia
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). The use and reporting of cluster analysis in health psychology: A review. British Journal of Health Psychology 10: 329-358.
- Romesburg, H. Clarles, Cluster Analysis for Researchers, 2004, 340 pp. ISBN 1411606175 ou publisher, reprint of 1990 edition published by Krieger Pub. Emissao… Uma tradução em japonês está disponível na Uchida Rokakuho Publishing Co., Ltd., Tóquio, Japão.
- Heyer, L. J., Kruglyak, S. and Yooseph, S., Exploring Expression Data: Identification and Analysis of Coexpressed Genes, Genome Research 9:1106-1115.
- the on-line textbook: Information Theory, inferência, and Learning Algorithms, by David J. C. MacKay includes chapters on k-means clustering, soft k-means clustering, and derivations including the E-M algorithm and the variational view of the E-M algorithm.
para agrupamento espectral :
- Jianbo Shi e Jitendra Malik,” normalized Cuts and Image Segmentation”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8), 888-905, August 2000. Disponível na página inicial de Jitendra Malik
- Marina Meila e Jianbo Shi, “Learning Segmentation with Random Walk”, Neural Information Processing Systems, NIPS, 2001. Disponível na página inicial de Jianbo Shi
para estimar o número de aglomerados:
- Can, F., Ozkarahan, E. A. (1990) “Concepts and effectiveness of the cover coefficient-based clustering methodology for text databases.”ACM Transactions on Database Systems. 15 (4) 483-517.
implementações de Software
Grátis
- o flexclust pacote para R
- YALE (Ainda Outro Ambiente de Aprendizagem): free software open-source para descoberta de conhecimento e mineração de dados, incluindo também um plugin para o cluster
- alguns Matlab arquivos de origem para o agrupamento aqui
- COMPACT – Comparativo Pacote para o agrupamento de Avaliação (também no Matlab)
- mixmod : Cluster Baseado Em Modelos E Análise Discriminatória. Code in C++, interface with Matlab and Scilab
- LingPipe Clustering Tutorial Tutorial for doing complete-and single-link clustering using LingPipe, a Java text data mining package distributed with source.Weka: Weka contém ferramentas para pré-processamento de dados, classificação, regressão, agrupamento, regras de associação e visualização. É também adequado para o desenvolvimento de novos sistemas de aprendizagem por máquina.