algorytmy FDTD i FDM do analizy MHOF
światło optyczne jest falą elektromagnetyczną w przyrodzie, a więc jego właściwości propagacyjne są regulowane przez prawa elektrodynamiki, które są zbiorczo znane jako równania Maxwella. Wiadomo, że kierowanie sygnałami świetlnymi w mhof za pomocą fotonicznych struktur bandgap opiera się na konstruktywnym efekcie interferencyjnym ze względu na okresowe ułożenie identycznych otworów powietrznych. Z drugiej strony, gdy otwory powietrzne stają się przypadkowe pod względem wielkości, lokalizacji lub obu, zachodzi zjawisko całkowitego wewnętrznego odbicia, a różnica indeksów między rdzeniem a okładziną zapewnia ograniczenie światła, a tym samym prowadzenie światła wzdłuż włókna. Chociaż charakterystyka propagacji skomplikowanych struktur, takich jak arbitralne MHOFs, nie może być łatwo obliczona przy użyciu metod analitycznych, istnieją sposoby numerycznego rozwiązywania problemów elektromagnetycznych.
w tej sekcji omówiono dwie techniki numeryczne metody FDTD (finite-difference Time-domain) i metody FDM (finite difference method), rozważając rozszerzenie analizy dziurawych włókien światłowodowych o dowolnych rozkładach otworów powietrza. Każda z tych technik ma pewne zalety. Stosując metodę FDTD, ciągłe pole elektromagnetyczne w skończonej objętości przestrzeni jest próbkowane w różnych punktach w sieci przestrzeni i w równo rozmieszczonych punktach próbkowania w czasie. Próbki danych w punktach są wykorzystywane do obliczeń numerycznych dozwolonych trybów, bez generowania fałszywych rozwiązań trybów, w danym falowodzie. Mimo że jest skuteczną techniką obliczania stałych propagacji trybów kierowanych, metoda FDTD nie jest dobrze przystosowana do oceny poszczególnych rozkładów pola trybów. Wynika to z faktu, że źródłem jest funkcja impulsowa w dziedzinie czasu obejmująca nieskończone spektrum, stąd rozwiązania rozkładu pola są superpozycją wszystkich możliwych trybów. Aby złagodzić ten problem ze stałymi propagacji dostępnymi w FDTD, Indywidualne rozkłady pól trybowych są uzyskiwane za pomocą FDM, który może szybko i wygodnie dostarczyć indywidualne rozwiązania pól trybowych.
FDTD zyskał znaczną popularność w ostatnich latach, ponieważ metoda ta zapewnia solidne rozwiązania, oparte na równaniach Maxwella, i może łatwo pomieścić złożone właściwości materiału. Dowolny obiekt materialny może być przybliżony przez budowanie komórek jednostkowych, dla których pozycje składników pola są usuwane z pożądanymi wartościami przenikalności i przepuszczalności. Po określeniu geometrii obiektu w obszarze symulacji numerycznej, warunek źródłowy jest modelowany gdzieś w tym regionie. Początkowo zakłada się, że wszystkie pola w domenie obliczeniowej są identyczne. Następnie fala incydentalna jest wymuszana, aby wejść do obszaru obliczeń numerycznych.
używając Układu Jednostek MKS, rozważmy najpierw równania curl Maxwella wyrażone jako:
gdzie ε jest stałą przenikalności elektrycznej w F/M, A μ jest stałą przenikalności magnetycznej w H/M. rozszerzając wyrażenia zwijania i zrównując podobne składniki, układ sześciu sprzężonych równań różniczkowych cząstkowych tworzy się do analizy FDTD oddziaływań fal elektromagnetycznych z ogólnymi obiektami trójwymiarowymi. Należy zauważyć, że składniki pola elektrycznego i magnetycznego (Ex, Ey, Ez, Hx, Hy i Hz) są wzajemnie powiązane. Oznacza to, że równania Maxwella nie dają bezpośrednio wartości pola elektrycznego i magnetycznego, ale raczej odnoszą się do szybkości zmiany wartości pola elektrycznego i magnetycznego.
przyjmując Centralne przybliżenie różnic skończonych dla pochodnych czasoprzestrzeni i czasu z dokładnością do drugiego rzędu, można opracować następujące przybliżenia jako reprezentatywne przykłady w trójwymiarowym (3D) formulacji FDTD:
Gdzie I, J, K I N są liczbami całkowitymi dla δx, δy, δz i δt, odpowiednio, jako przyrosty przestrzeni i czasu .
ponieważ włókna optyczne, takie jak MHOFs, na ogół nie mają zmian wzdłuż kierunku propagacji, a zmiany właściwości materiału są ograniczone do kierunków poprzecznych, jak pokazano na fig .3, formułowanie 3D FDTD można uprościć do kompaktowego dwuwymiarowego (2D) algorytmu FDTD. Stosując notację fazową ze stałą propagacji osiowej (β), pochodne cząstkowe pierwszego rzędu względem z są zastępowane przez-jß, ponieważ zależność z pól jest jak exp (- jßz). A dwa sąsiadujące pola wymagane dla pochodnych pierwszego rzędu w obszarze przestrzeni dyskretnej mogą być reprezentowane przez pole w środkowym punkcie między nimi. Opierając się na tych dwóch faktach, otrzymano następujący wzór jako przykład:
powstały algorytm 2D wykorzystuje znaczną redukcję wymaganej alokacji pamięci komputera i czasu pracy. Tak więc, do komputerowego obliczania dowolnych falowodów, które są jednolite wzdłuż kierunku propagacji fali, wystarczy jedynie modelowanie przekrojów falowodów.
wraz z tym wydajnym algorytmem, nieskończone media w przestrzeni 2D dla dowolnego obiektu elektromagnetycznego muszą być starannie modelowane, ponieważ pamięć komputera jest ograniczona w obszarze obliczeniowym nawet przy zaawansowanej obecnej technologii. W celu modelowania regionów rozciągających się do nieskończoności, idealnie dopasowana warstwa (PML) jako wysoce efektywny absorbujący warunek graniczny (ABC) jest zaprojektowana na zewnętrznej granicy kraty dziedziny obliczeniowej. Idealnie, medium absorbujące jest tak grube jak kilka komórek sieciowych, wysoce absorbujące, bez odbicia dla wszystkich fal uderzających i skuteczne w pełnym zakresie długości fal roboczych.
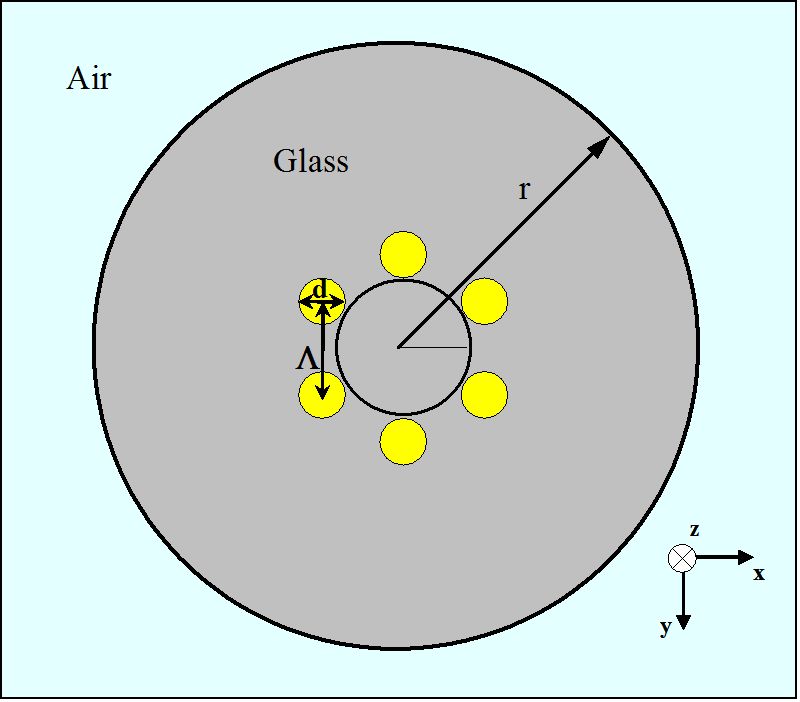
Rysunek 3.
schemat przekroju MHOF z jedną warstwą otworów powietrznych w układzie sześciokątnym
podobnie jak w przypadku opracowania algorytmu FDTD, formułę FDM można wyprowadzić ze sprzężonych równań Maxwella . Dla fal ciągłych w mediach liniowych i izotropowych połączenie Eqs (2) i (3) daje następujące równanie fali wektorowej:
gdzie n to współczynnik załamania światła, a K0 to stała propagacji w wolnej przestrzeni. Wiele urządzeń falowodowych, takich jak włókna optyczne, może być postrzegane jako z-niezmienne lub fragmentarycznie z-niezmienne struktury. Dla tych struktur współczynnik załamania światła n (x,y,z) zmienia się powoli wzdłuż kierunku propagacji z, który jest ważny dla większości fotonicznych urządzeń z falą kierowaną. Wykorzystując tożsamość wektorową∇×∇×=∇(∇⋅)−∇2, Eq (8)można zapisać jako
również przy rozsądnym założeniu nieistotnej zależności czasowej wzdłuż osi Z, sformułowanie FDM jak w EQ (9) może być zaimplementowane przez zastąpienie pochodnych przestrzennych skończonymi przybliżeniami różnicowymi. Tutaj należy zauważyć, że składowa poprzeczna (9) jest
gdzie indeks „T” oznacza drążka składniki. Ponieważ składnik Podłużny można łatwo uzyskać przez zastosowanie następującego ograniczenia zerowej dywergencji (prawo Gaussa) :
skĹ 'adniki poprzeczne wystarczajÄ … do opisania peĹ’ nych wektorowych Natur pola elektromagnetycznego w falowodzie optycznym.
do wstępnego badania właściwości naprowadzających MHOFs, światłowód pokazany na rysunku 3 jest analizowany komputerowo. Ogólnie rzecz biorąc, geometrię MHOF można opisać za pomocą dwóch parametrów, długości skoku (Λ) i średnicy (d), jak pokazano na rysunku 3. Tutaj długość skoku to odległość między środkami dwóch najbliższych otworów powietrznych o cylindrycznym kształcie. Dla MHOF z fig. 3, każdy mały otwór powietrza ma średnicę 1,4 µm, co stanowi sześciokąt o Λ = 1,7 µm. Szklana część otaczająca sześć otworów powietrznych w żółtych regionach ma współczynnik załamania światła 1,45. Przyjmuje się, że promień zewnętrzny (r) włókna dziurawego wynosi 10 µm. Poza tym zewnętrznym obszarem MHOF jest powietrze.
po zdefiniowaniu przekroju dziurawego włókna w odpowiedniej dziedzinie obliczeń, symulację FDTD można przeprowadzić z kilkoma określonymi parametrami, takimi jak τ w definiowaniu Źródła Gaussa, Δt w symulacji stabilnej, całkowita liczba (ntot) kroków czasowych dla pobierania danych w dziedzinie czasu i rozsądne wartości β. W tym przypadku, aby uniknąć rozbieżności numerycznych i zapewnić stabilność algorytmu FDTD, należy wybrać odpowiedni Δt, aby spełnić następujący warunek stabilności:
gdzie cM jest maksymalną prędkością fazową fali w danym modelu numerycznym. Podsumowując mechanizm analizy FDTD, symulacja komputerowa przebiega w następujący sposób:
-
wybierz odpowiednie wartości parametrów (τ, Δt, ntot i β)
-
próbkowanie danych komponentu pola w dziedzinie czasu
-
weź transformatę Fouriera danych czasu
-
uzyskaj dane widmowe składnika pola
-
tryb wyboru częstotliwości związane z wartością β
-
zbieraj dane β i częstotliwości trybu
-
Stwórz wykres indeksu trybu a długość fali
Rysunek 4 ilustruje charakterystyczne krzywe, które uzyskuje się z FDTD obliczenia, dla pierwszych trzech trybów niższego rzędu mhof określonych na rysunku 3.
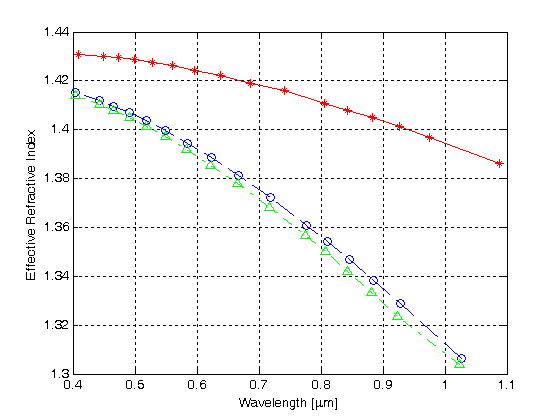
Rysunek 4.
efektywny współczynnik załamania względem długości fali dla pierwszych trzech trybów w MHOF z jedną warstwą otworów powietrznych
czerwona krzywa z symbolami gwiazd przedstawia znormalizowaną stałą propagacji dla pierwszego trybu w porównaniu z długością fali, podczas gdy niebieskie i zielone krzywe pokazują znormalizowane stałe propagacji odpowiednio dla drugiego i trzeciego trybu. Wyniki wskazują, że HMOF z pojedynczą sześciokątną warstwą okładzinową z otworem powietrznym obsługuje prowadzenie wielomodowe.