co to jest analiza klastra?
Analiza klastrów jest analizą eksploracyjną, która próbuje zidentyfikować struktury w danych. Analiza klastrów nazywana jest również analizą segmentacji lub analizą taksonomiczną. Dokładniej, próbuje zidentyfikować jednorodne grupy przypadków, jeśli grupowanie nie jest wcześniej znane. Ponieważ jest rozpoznawalny, nie dokonuje rozróżnienia między zmiennymi zależnymi i niezależnymi. Różne metody analizy klastrów oferowane przez SPSS mogą obsługiwać dane binarne, nominalne, porządkowe i skalowane (interwał lub stosunek).
Analiza klastrowa jest często stosowana w połączeniu z innymi analizami (takimi jak Analiza dyskryminacyjna). Badacz musi być w stanie zinterpretować analizę klastra w oparciu o ich zrozumienie danych, aby określić, czy wyniki uzyskane przez Analizę są rzeczywiście znaczące.
typowe pytania badawcze odpowiedzi na analizę klastra są następujące:
- Medycyna – jakie są klastry diagnostyczne? Aby odpowiedzieć na to pytanie, badacz opracowałby kwestionariusz diagnostyczny, który zawiera możliwe objawy (na przykład w psychologii, lęku, depresji itp.). Analiza klastra może następnie zidentyfikować grupy pacjentów, które mają podobne objawy.
- Marketing – jakie są segmenty klientów? Aby odpowiedzieć na to pytanie badacz rynku może przeprowadzić ankietę obejmującą potrzeby, postawy, dane demograficzne i zachowania klientów. Badacz może następnie wykorzystać analizę klastra do identyfikacji jednorodnych grup klientów, które mają podobne potrzeby i postawy.
- Edukacja – jakie grupy studenckie wymagają szczególnej uwagi? Badacze mogą mierzyć cechy psychologiczne, predyspozycje i osiągnięcia. Analiza klastra może następnie określić, jakie jednorodne grupy istnieją wśród studentów (na przykład, osoby osiągające wysokie wyniki we wszystkich przedmiotach lub studenci, którzy wyróżniają się w niektórych przedmiotach, ale nie w innych).
- Biologia – jaka jest Taksonomia gatunków? Naukowcy mogą zebrać zestaw danych o różnych roślinach i zauważyć różne atrybuty ich fenotypów. Analiza klastrów może grupować te obserwacje w szereg klastrów i pomóc w budowaniu taksonomii grup i podgrup podobnych roślin.
inne techniki, które warto wypróbować w celu zidentyfikowania podobnych grup obserwacji, to analiza Q, skalowanie wielowymiarowe (MDS) i analiza klas utajonych.
Analiza klastrów w SPSS
nasze pytanie badawcze dotyczące tej przykładowej analizy klastrów jest następujące:
jakie jednorodne klastry uczniów powstają w oparciu o znormalizowane wyniki testów z matematyki, czytania i pisania?
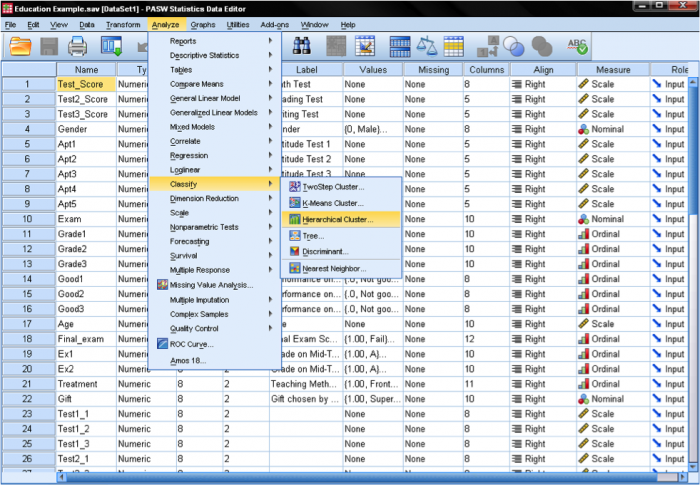
w SPSS analizy klastrów można znaleźć w analizować/klasyfikować…. SPSS oferuje trzy metody analizy klastra: Klaster K-Means, Klaster hierarchiczny i klaster dwustopniowy.
k-means cluster to metoda szybkiego klastrowania dużych zbiorów danych. Badacz z góry określa liczbę klastrów. Jest to przydatne do testowania różnych modeli z inną zakładaną liczbą klastrów.
Klaster hierarchiczny jest najczęstszą metodą. Generuje serię modeli z rozwiązaniami klastrów od 1 (wszystkie przypadki w jednym klastrze) do n (każdy przypadek jest pojedynczym klastrem). Klaster hierarchiczny działa również ze zmiennymi w przeciwieństwie do przypadków; może gromadzić zmienne razem w sposób nieco podobny do analizy czynnikowej. Ponadto hierarchiczna analiza klastrów może obsługiwać dane nominalne, porządkowe i skalowe; nie zaleca się jednak mieszania różnych poziomów pomiaru.
dwuetapowa analiza klastra identyfikuje grupy, uruchamiając najpierw wstępne klastrowanie, a następnie uruchamiając metody hierarchiczne. Ponieważ korzysta z szybkiego algorytmu klastra z góry, może obsługiwać duże zbiory danych, które zajęłyby dużo czasu, aby obliczyć za pomocą hierarchicznych metod klastrowych. Pod tym względem jest to połączenie dwóch poprzednich podejść. Dwustopniowe grupowanie może obsługiwać dane skalowane i porządkowe w tym samym modelu i automatycznie wybiera liczbę klastrów.
hierarchiczna analiza klastrów przebiega w trzech podstawowych krokach: 1) Oblicz odległości, 2) Połącz klastry i 3) Wybierz rozwiązanie, wybierając odpowiednią liczbę klastrów.
najpierw musimy wybrać zmienne, na których bazujemy nasze klastry. W oknie dialogowym do listy zmiennych dodajemy testy z matematyki, czytania i pisania. Ponieważ chcemy klastrować przypadki, zostawiamy resztę znaczników na domyślnym.
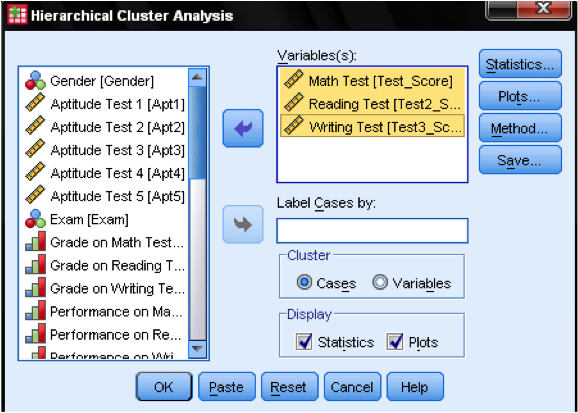
w oknie dialogowym statystyki … możemy określić, czy chcemy wyprowadzić macierz zbliżeniową( są to odległości obliczone w pierwszym etapie analizy) oraz przewidywany skład klastrów przypadków w naszych obserwacjach. Ponownie, zostawiamy wszystkie ustawienia na domyślne.

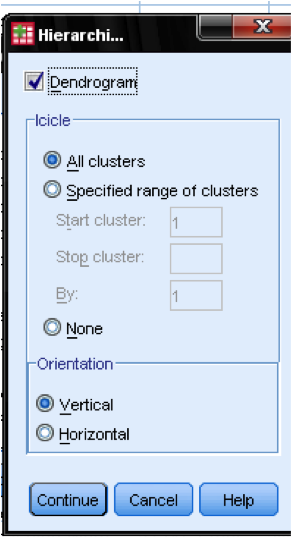
w oknie dialogowym wykresy … powinniśmy dodać Dendrogram. Dendrogram graficznie pokaże, w jaki sposób klastry są łączone i pozwoli nam zidentyfikować odpowiednią liczbę klastrów.
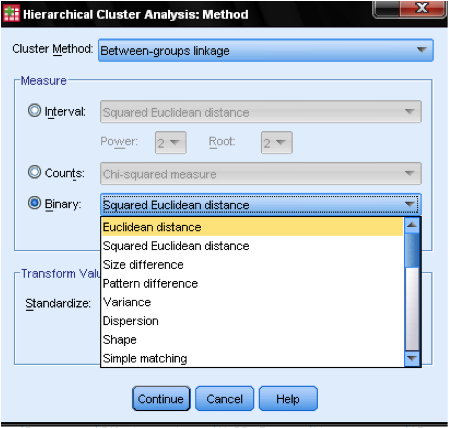
okno dialogowe Metoda … pozwala nam określić miarę odległości i metodę klastrowania. Po pierwsze, musimy zdefiniować prawidłową miarę odległości. SPSS oferuje trzy duże bloki miar odległości dla danych interwałowych (skala), liczonych (porządkowych) i binarnych (nominalnych).
dla danych interwałowych najczęściej jest kwadratową odległością euklidesową. Opiera się na odległości euklidesowej między dwiema obserwacjami, która jest pierwiastkiem kwadratowym sumy kwadratowych odległości. Ponieważ odległość euklidesowa jest kwadratowa, zwiększa znaczenie dużych odległości, osłabiając znaczenie małych odległości.

jeśli mamy dane porządkowe (liczby) możemy wybrać pomiędzy Chi-kwadrat lub standardowy chi-kwadrat zwany Phi-kwadrat. Dla danych binarnych powszechnie stosuje się kwadratową odległość euklidesową.

w naszym przykładzie wybieramy Przedział i kwadratową odległość euklidesową.
następnie musimy wybrać metodę klastra. Zazwyczaj do wyboru są powiązania między grupami (odległość między klastrami to średnia odległość wszystkich punktów danych w tych klastrach), najbliższy sąsiad (pojedyncze powiązanie: odległość między klastrami to najmniejsza odległość między dwoma punktami danych), najdalszy sąsiad (kompletne połączenie: odległość to największa odległość między dwoma punktami danych) i metoda Warda (odległość to odległość wszystkich klastrów do Wielkiej średniej próbki). Pojedyncze połączenie działa najlepiej z długimi łańcuchami klastrów, podczas gdy kompletne połączenie działa najlepiej z gęstymi Plamami klastrów. Połączenie między grupami działa z obydwoma typami klastrów. Zaleca się najpierw użycie pojedynczego połączenia. Chociaż pojedyncze powiązanie ma tendencję do tworzenia łańcuchów klastrów, pomaga w identyfikacji wartości odstających. Po wykluczeniu tych wartości odstających możemy przejść do metody Warda. Metoda Warda wykorzystuje wartość F (jak w ANOVA), aby zmaksymalizować znaczenie różnic między klastrami.
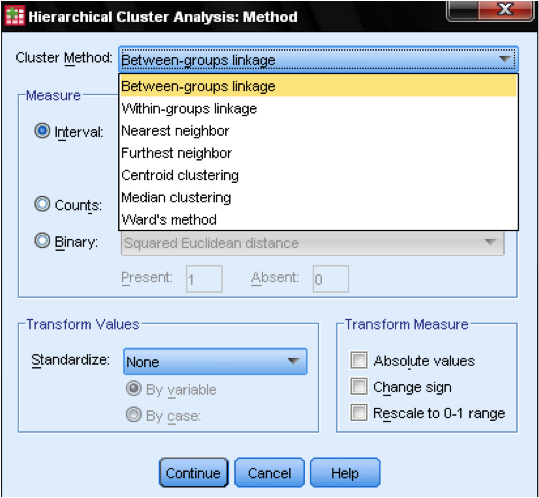
ostatnią kwestią jest standaryzacja. Jeśli zmienne mają różne skale i środki, możemy chcieć znormalizować albo wyniki Z, albo centrując skalę. Możemy również przekształcić wartości do wartości bezwzględnych, jeśli mamy zestaw danych, w którym może to być właściwe.