według Noama Chomosky ’ ego istnieją cztery rodzaje gramatyk − Typ 0, Typ 1, Typ 2 i typ 3. Poniższa tabela pokazuje, jak różnią się one od siebie−
| Typ gramatyki | Gramatyka zaakceptowana | język zaakceptowany | Automat |
|---|---|---|---|
| Typ 0 | gramatyka Nieograniczona | język rekurencyjnie wyliczany | maszyna Turinga |
| Typ 1 | gramatyka kontekstowa | język kontekstowy | automat liniowy |
| Typ 2 | gramatyka bez kontekstu | Język bez kontekstu | Automat Pushdown |
| Typ 3 | Gramatyka regularna | język regularny |
spójrz na poniższą ilustrację. Pokazuje zakres każdego typu gramatyki –
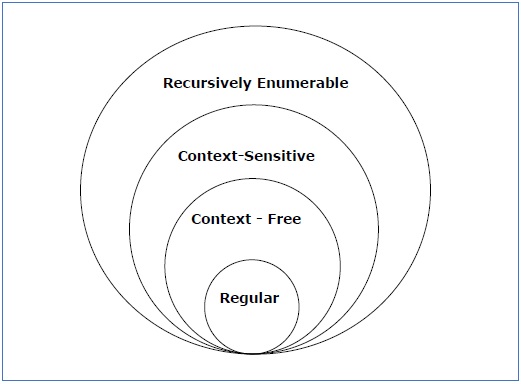
Gramatyka typu 3
gramatyki typu 3 generują języki regularne. Gramatury typu 3 muszą mieć po lewej stronie pojedynczy nie-terminal i po prawej stronie składający się z pojedynczego terminala lub pojedynczego terminala, po którym następuje pojedynczy nie-terminal.
produkcje muszą mieć postać x → A lub X → aY
gdzie X, Y ∈ N (Non terminal)
i A ∈ T (Terminal)
reguła s → ε jest dozwolona, jeśli S nie pojawia się po prawej stronie żadnej reguły.
przykład
X → ε X → a | aYY → b
Gramatyka typu 2
gramatyki typu 2 generują języki wolne od kontekstu.
produkcje muszą mieć postać a → γ
gdzie A ∈ N (Non-terminal)
i γ ∈ (T ∪ N)* (ciąg terminali i nie-terminali).
te języki generowane przez te gramatyki są rozpoznawane przez niedeterministyczny automat wypychania.
przykład
S → X a X → a X → aX X → abc X → ε
Gramatyka typu 1
gramatyki typu 1 generują języki wrażliwe na kontekst. Produkcje muszą mieć postać
α a β → α γ β
gdzie A ∈ N (Non-terminal)
i α, β, γ ∈ (T ∪ N)* (ciągi zacisków i nie-zacisków)
ciągi α i β mogą być puste, ale γ musi być niepuste.
reguła s → ε jest dozwolona, jeśli S nie pojawia się po prawej stronie żadnej reguły. Języki generowane przez te gramatyki są rozpoznawane przez liniowy automat Ograniczony.
przykład
AB → AbBc A → bcA B → b
Gramatyka typu 0
gramatyki typu 0 generują rekurencyjnie wyliczalne języki. Produkcje nie mają żadnych ograniczeń. Są to gramatyki o dowolnej strukturze fazowej, w tym wszystkie gramatyki formalne.
generują języki rozpoznawane przez maszynę Turinga.
produkcje mogą mieć postać α → β, gdzie α jest ciągiem terminali i nieterminali z co najmniej jednym Nie-terminalem, a α nie może być null. β jest ciągiem terminali i nie-terminali.
Przykład
S → ACaB Bc → acB CB → DB aD → Db