fdtd-og FDM-algoritmer for MHOF-analysen
Optisk lys er elektromagnetisk bølge i naturen, og dermed er dets forplantningsegenskaper styrt av elektrodynamikkloven som kollektivt er Kjent Som Maxwells ligninger. Det er kjent at styring av lyssignaler I MHOF med fotoniske bandgapstrukturer er avhengig av konstruktiv interferenseffekt på grunn av periodisk arrangement av identiske lufthull. På den annen side, når lufthullene blir tilfeldige i størrelse, plassering eller begge deler, skjer fenomenet total intern refleksjon og indeksforskjellen mellom kjernen og kledningen gir lysinneslutning og dermed veiledning av lys langs fiberen. Selv om forplantningsegenskapene til kompliserte strukturer som vilkårlig MHOFs ikke kan beregnes enkelt ved hjelp av analytiske metoder, er det måter å løse elektromagnetiske problemer numerisk.
i denne delen, to numeriske teknikker for endelig-difference time-domain (FDTD) og endelig difference method (FDM) er adressert vurderer utvidelse til analyse av holey optiske fibre med vilkårlige luft-hull fordelinger. Hver av disse teknikkene har visse fordeler. VED HJELP AV fdtd-metoden blir det kontinuerlige elektromagnetiske feltet i et begrenset volum plass samplet på forskjellige punkter i et romgitter og på like fordelte samplingspunkter i tid. De samplede dataene på punktene brukes til numeriske beregninger av tillatte moduser, uten å generere falske modusløsninger, i en gitt bølgeleder. Til tross for å være en effektiv teknikk for beregning av forplantningskonstanter av guidede moduser, ER FDTD-metoden ikke godt egnet for evaluering av individuelle modusfeltfordelinger. Dette skyldes at kilden er en impulsfunksjon i tidsdomenet som dekker et uendelig spektrum, og dermed er feltfordelingsløsninger superposisjon av alle mulige moduser. For å lindre dette problemet med forplantningskonstanter tilgjengelig fra FDTD, oppnås individuelle modusfeltfordelinger ved HJELP AV FDM, som raskt og enkelt kan gi individuelle modusfeltløsninger.
FDTD har fått betydelig popularitet de siste årene, fordi denne metoden gir robuste løsninger, basert På Maxwells ligninger, og kan lett imøtekomme komplekse materielle egenskaper. Et vilkårlig materialobjekt kan tilnærmes ved å bygge opp enhetsceller for hvilke feltkomponentposisjoner er anordnet med de ønskede verdier av permittivitet og permeabilitet. Når objektets geometri er spesifisert i den numeriske simuleringsregionen, modelleres kildetilstanden et sted i regionen. I utgangspunktet antas det at alle felt i beregningsdomenet er identisk null. Deretter håndheves en hendelsesbølge for å angi det numeriske beregningsområdet.
Ved HJELP AV mks-systemet av enheter, la Oss først vurdere Maxwells krølleligninger uttrykt som:
der ε er den elektriske permittivitetskonstanten i f/M og μ er den magnetiske permeabilitetskonstanten i h / M. ved å utvide Krølleuttrykkene og likne de lignende komponentene, dannes systemet med seks koblede partielle differensialligninger for FDTD-ANALYSEN av elektromagnetiske bølgeinteraksjoner med generelle tredimensjonale objekter. Det skal bemerkes at de elektriske og magnetiske feltkomponentene (Ex, Ey, Ez, Hx, Hy Og Hz) er interrelaterte. Det Vil Si At Maxwells ligninger ikke direkte gir elektriske og magnetiske feltverdier, men heller relaterer endringshastigheten mellom elektriske og magnetiske feltverdier.
Ved Å Vedta sentral endelig differansetilnærming for rom-og tidderivater med nøyaktighet til andre rekkefølge, kan følgende tilnærminger som representative eksempler i en tredimensjonal (3D) FDTD-formulering utvikles:
hvor i, j, k og n er heltall for Δx, Δy, Δz, og Δt, henholdsvis, som rom og tid intervaller .
siden optiske fibre som MHOFs generelt ikke har noen variasjoner langs forplantningsretningen, og variasjoner av materialegenskaper er begrenset til tverrretningen som vist i Figur 3, kan 3d FDTD-formuleringen forenkles til den kompakte todimensjonale (2D) fdtd-algoritmen . Ved å bruke fasornotasjon med den aksiale forplantningskonstanten (β) erstattes førstegangs partiellderivater med hensyn til z med-jß, fordi z-avhengigheten av felt er som exp (- jß). Og to tilstøtende felt som kreves for førstegangsderivatene i den diskretiserte romregionen, kan representeres av et felt midtpunktet mellom dem. Basert på disse to fakta, er følgende formulering som et eksempel oppnådd:
Den Resulterende 2D-ALGORITMEN utnytter betydelig reduksjon i den nødvendige dataminnetildelingen og kjøretiden. For datamaskinberegning av vilkårlig bølgeledere som er ensartede langs bølgeutbredelsesretningen, er det derfor bare modellering av tverrsnittene av bølgeledere som er tilstrekkelig.
sammen med denne effektive algoritmen må uendelige medier I 2D-rommet for et vilkårlig elektromagnetisk objekt modelleres nøye, fordi datamaskinens minne er begrenset i beregningsområdet selv med avansert nåværende teknologi. For å modellere regioner som strekker seg til uendelig, er et perfekt tilpasset lag (pml) som en svært effektiv absorberende grensetilstand (ABC) utformet ved den ytre gittergrensen til et beregningsdomene. Ideelt sett er det absorberende mediet bare så tykt som noen få gitterceller, svært absorberende, refleksjonsløst for alle impingingbølger, og effektivt over hele spekteret av driftsbølgelengder.
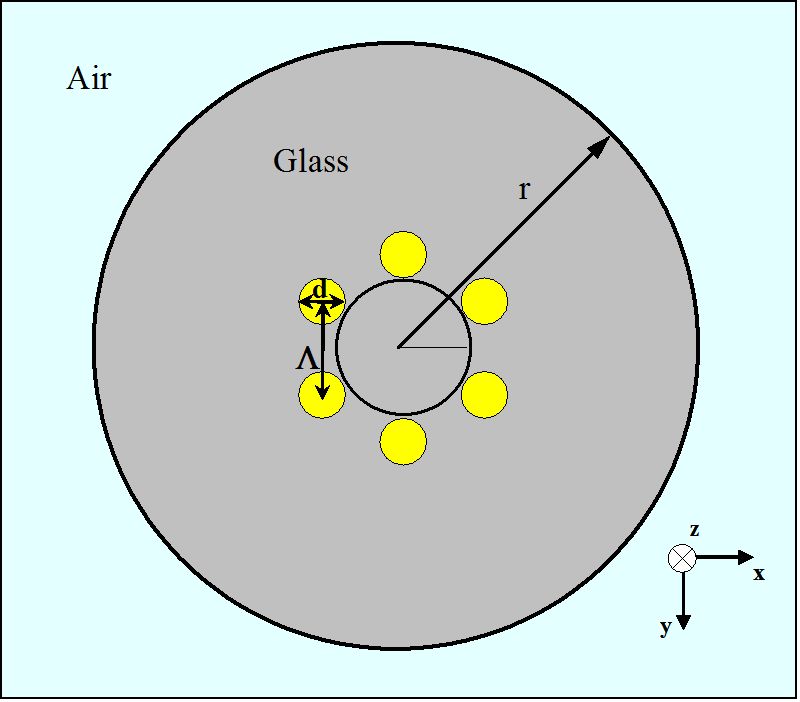
Figur 3.
Skjematisk av et tverrsnitt for EN MHOF med ett lag med lufthull i et sekskantet arrangement
På Samme måte som utviklingen AV fdtd-algoritmen, KAN fdm-formuleringen avledes fra de koblede Maxwells ligninger . For kontinuerlige bølger i lineære og isotropiske medier resulterer kombinering Av Eq (2) og (3) i følgende vektorielle bølgeligning:
hvor n er brytningsindeksen og k0 er forplantningskonstanten i ledig plass. Mange bølgeledere, som optiske fibre, kan ses som z-invariant eller stykkevis z-invariant strukturer. For disse strukturene varierer brytningsindeksen n(x, y,z) sakte langs forplantningsretningen z, som er gyldig for de fleste fotoniske guidede bølgeinnretninger. Ved å bruke vektoridentiteten til∇×∇×=∇(∇⋅)−∇2, Eq (8) kan skrives som
Også med rimelig antagelse om ubetydelig tidsavhengighet langs z-aksen, kan fdm-FORMULERINGEN som i eq (9) implementeres ved å erstatte romlige derivater med endelige differansetilnærminger. Her er det bemerket at den tverrgående del av (9) er
hvor senket skrift «t» står for den tverrgående komponenter. Siden den langsgående komponenten lett kan oppnås ved anvendelse av følgende null divergens (Gauss lov) begrensning:
de tverrgående komponentene er tilstrekkelige til å beskrive det elektromagnetiske feltets fullvektorielle natur i en optisk bølgeleder.
For den første undersøkelsen av veiledningsegenskapene Til MHOFs, er den optiske fiberen vist i Figur 3 datamaskinanalysert. GENERELT KAN MHOF-geometrien beskrives med to parametere, stigningslengde (Λ) og diameter (d), som angitt i Figur 3. Her er tonelengden avstanden mellom sentre av to nærmeste lufthull med sylindrisk form. FOR MHOF i figur 3 har hvert lite lufthull en diameter på 1.4 µ, som utgjør en sekskant med Λ = 1.7 µ. Glasspartiet rundt de seks lufthullene i de gule områdene har en brytningsindeks på 1,45. Den ytre radiusen (r) til holey fiber antas å være 10 µ. OGSÅ UTSIDEN av MHOF er luft.
NÅR tverrsnittet av et holey fiber er definert i et riktig beregningsdomene, kan FDTD-simuleringen gjennomføres med flere spesifiserte parametere, som for eksempel τ ved definering Av En Gaussisk kilde, Δ for stabil simulering, totalt antall (ntot) tidstrinn for prøvetaking av data i tidsdomenet og rimelige verdier av β. Her, for å unngå numerisk divergens og sikre stabiliteten TIL fdtd-algoritmen, må det velges en passende Δ for å tilfredsstille følgende stabilitetsforhold:
hvor cM er maksimal bølgefasehastighet innenfor en gitt numerisk modell. Oppsummering av mekanismen bak fdtd-analysen, fortsetter datasimuleringen med følgende trinn:
-
Velg passende parameterverdier (τ, Δ, ntot og β)
-
datautvalg av en feltkomponent i tidsdomenet
-
Ta Fourier-transformasjonen av tidsdataene
-
Få spektrale data for en feltkomponent
-
Velg modusfrekvenser knyttet til β verdi
-
Samle inn β og modusfrekvensdata
-
Lag et plott av modusindeks versus bølgelengde
Figur 4 illustrerer de karakteristiske kurver, som er oppnådd FRA FDTD beregning, for DE tre første lavere rekkefølge moduser AV MHOF definert i Figur 3.
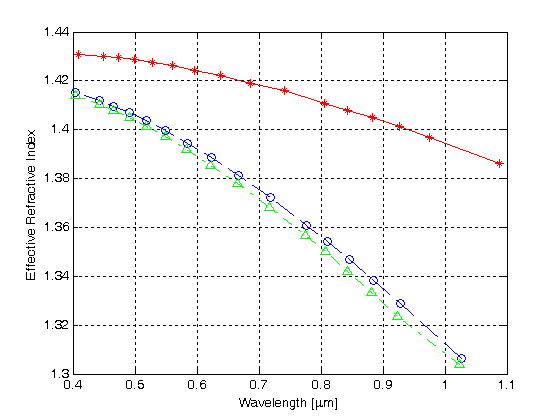
Figur 4.
Effektiv brytningsindeks versus bølgelengde for de tre første modusene I EN MHOF med ett lag med lufthull
den røde kurven med stjernesymbolene plotter den normaliserte forplantningskonstanten for den første modusen versus bølgelengden, mens de blå og grønne kurvene viser de normaliserte forplantningskonstantene for henholdsvis den andre og den tredje modusen. Resultatene indikerer at HMOF med et enkelt sekskantet lufthull kledning lag støtter multimode guiding.