4.2線形回帰モデルの係数の推定
実際には、母集団回帰線の切片\(\beta_0\)と傾き\(\beta_1\)は不明である。 したがって,未知のパラメータの両方を推定するためにデータを用いなければならない。 以下では、これがどのように達成されるかを実証するために、現実世界の例を使用します。 私たちは、カリフォルニアの学校で測定された学生と教師の比率にテストの点数を関連付けたいと考えています。 テストスコアは、五年生のための読書と数学のスコアの地区全体の平均です。 ここでも、クラスのサイズは、生徒の数を教師の数(生徒と教師の比率)で割ったものとして測定されます。 データについては、California Schoolデータセット(CASchools)には、Rを使用したApplied Econometricsの頭字語であるAERと呼ばれるRパッケージが付属しています(Kleiber and Zeileis2020)。 Installでパッケージをインストールした後。パッケージ(”AER”)とそれをライブラリ(AER)に添付すると、データセットは関数data()を使用してロードできます。
## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)パッケージがインストールされると、それはlibrary()で呼び出されたときにそれ以上の機会に使用できるようになります。installを実行する必要はありません。パッケージ()再び!
私たちが扱っているオブジェクトの種類を知ることは興味深いです。class()はオブジェクトのクラスを返します。 オブジェクトのクラスに応じて、いくつかの関数(例えば、plot()とsummary())は異なる動作をします。
オブジェクトCASchoolsのクラスを確認しましょう。
class(CASchools)#> "data.frame"CASchoolsはクラスデータであることが判明しました。フレームは、特に回帰分析を実行するために、で動作するように便利な形式です。
head()の助けを借りて、データの最初の概要を取得します。 この関数は、データセットの最初の6行のみを表示し、コンソール出力の過密を防ぎます。
head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4データセットはたくさんの変数で構成されており、そのほとんどは数値であることがわかります。ところで、class()とhead()の代わりにstr()がありますstr()これは’structure’から推定され、オブジェクトの包括的な概要を提供します。 試してみて!
CASchoolsに戻って、私たちが興味を持っている二つの変数(すなわち、平均テストスコアおよび学生-教師の比率)は含まれていません。 ただし、提供されたデータから両方を計算することは可能です。 生徒と教師の比率を得るには、生徒の数を教師の数で単純に除算します。 平均テストスコアは、読書のためのテストスコアと数学テストのスコアの算術平均です。 次のコードチャンクは、2つの変数をベクトルとして構築する方法と、それらがCASchoolsにどのように追加されるかを示しています。
# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2 実行した場合head(CASchools)再び、STRとscoreという名前の追加列として関心のある2つの変数を見つけます(これを確認してください!).
教科書の表4.1は、テストの点数と生徒と教師の比率の分布をまとめたものです。 同様の結果を生成するために使用できるいくつかの関数があります。,
-
mean()(指定された数値の算術平均を計算します),
-
sd()(サンプル標準偏差を計算します),
-
quantile()(データの指定されたサンプル分位数のベクトルを返します)。
次のコードチャンクは、これを達成する方法を示しています。 まず、CASchoolsの列STRとscoreの要約統計量を計算します。 良い出力を得るために、データ内の測定値を収集します。DistributionSummaryという名前のフレーム。
# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999サンプルデータについては、plot()を使用します。 これにより、単なる数字を見ることで発見するのが難しい外れ値など、データの特性を検出することができます。 今回は、plot()の呼び出しにいくつかの追加の引数を追加します。
plot()の呼び出しの最初の引数score~STRは、y軸とx軸の変数を記述する式です。 ただし、今回は2つの変数は別々のベクトルに保存されず、CASchoolsの列です。 したがって、引数dataが正しく指定されていないと、Rはそれらを見つけません。 データは、データの名前に従っている必要があります。変数が属するフレーム、この場合はCASchools。 さらに引数を使用してプロットの外観を変更します。mainはタイトルを追加しますが、xlabとylabは両方の軸にカスタムラベルを追加します。
plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")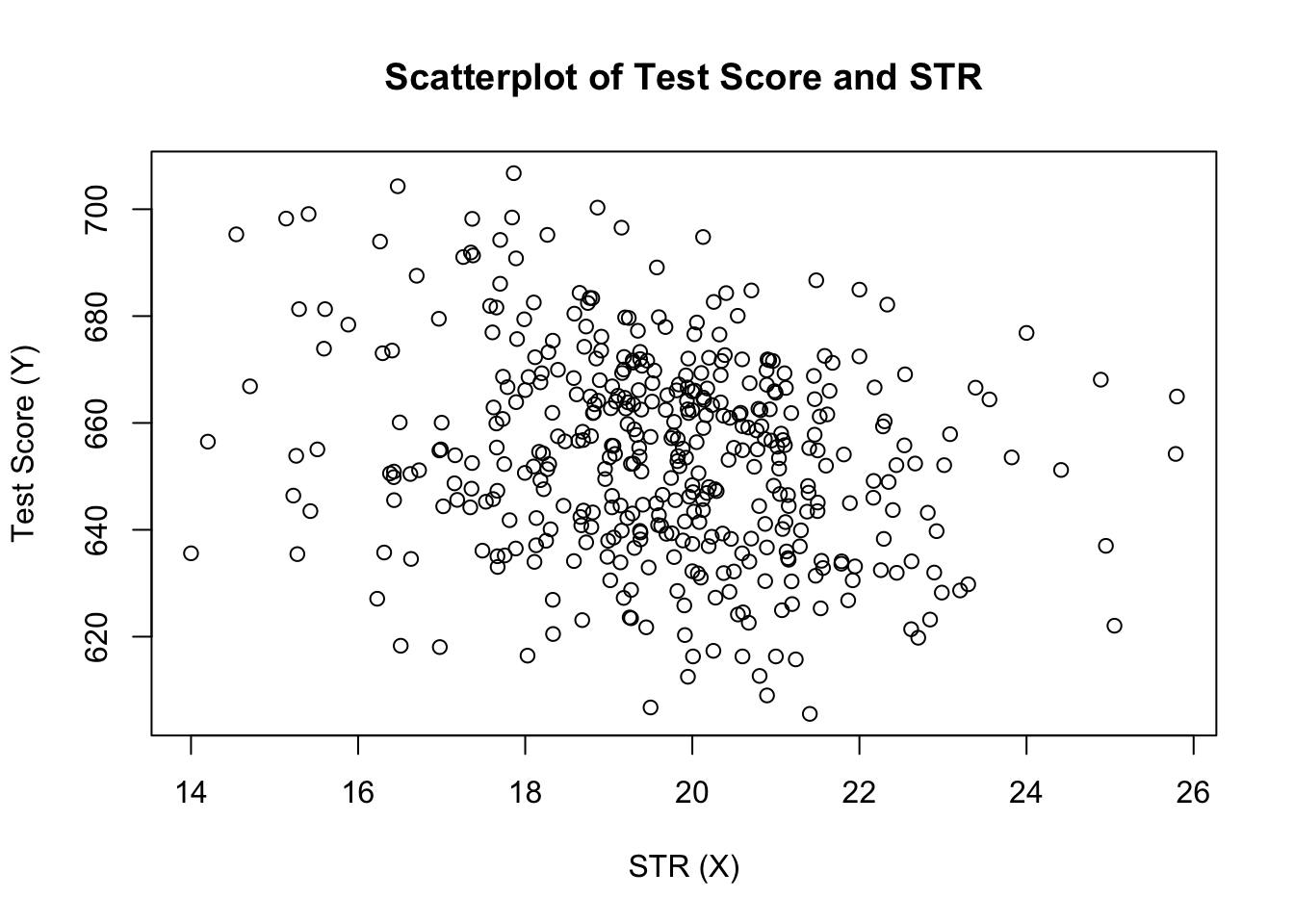
プロット(本の図4.2)は、学生と教師の比率とテストスコアに関するすべての観測値の散布図を示しています。 点は強く散乱され、変数は負の相関があることがわかります。 つまり、大きなクラスではテストの点数が低くなることを期待しています。
関数cor()(参照?corは、2つの数値ベクトル間の相関関係を計算するために使用できます。
cor(CASchools$STR, CASchools$score)#> -0.2263627散布図がすでに示唆しているように、相関は負ですが、むしろ弱いです。
今直面している課題は、データに最も適した線を見つけることです。 当然私達は写実的な点検および相関関係の分析と単に付き、次にeyeballingによって最もよい適切なラインを選ぶことができます。 しかし、これはむしろ主観的であろう:異なるオブザーバーは異なる回帰線を描くだろう。 このため、私たちはあまり恣意的ではない技術に興味があります。 このような手法は、通常の最小二乗法(OLS)推定によって与えられる。
通常の最小二乗推定器
OLS推定器は、推定された回帰直線が観測されたデータポイントにできるだけ”近い”ように回帰係数を選択します。 ここで、近さは、与えられた\(X\)を予測する際に行われた2乗の間違いの合計によって測定されます。 \(B_0\)と\(b_1\)を\(\beta_0\)と\(\beta_1\)の推定量とする。 次に、推定誤差の二乗和は次のように表すことができます
\
単純回帰モデルのOLS推定量は、上記の式を最小化する切片と傾きの推定量のペアです。 両方のパラメータに対するOLS推定量の導出は、本の付録4.1に記載されています。 結果は、キーコンセプト4.2に要約されています。単純線形回帰モデルにおける傾き\(\beta_1\)と切片\(\beta_0\)のOLS推定量は、OLS予測値\(\widehat{Y}_i\)と残差\(\hat{u}_i\)は\
推定切片\(\hat{\widehat{Y}_i\)と残差\(\hat{\widehat{Y}_i\)である。\(\hat{\widehat{Y}_i\)と残差\(\hat{\widehat{Y}_i\)と残差\(\hat{\widehat{Y}_i\)と残差\(\hat{\widehat{Y}_i\)と残差\(\hat{\widehat{Y}_i\)と残差\(\hat{\widehat{Y}_i\)と残差\(\hat{\widehat{Y}_i\)である。\(\Hat{\beta}_0\)、勾配パラメータ\(\hat{\beta}_1\)、および残差\(\Left(\Hat{U}_I\Right)\)は、\(x_i\)および\(y_i\)、\(i\)、\(の観測値のサンプルから計算されます。\(\Hat{U}_I\)、\(\Hat{U}_I\)、\(\Hat{U}_I\)、\(\Hat{U}_I\)、\(\Hat{u}_I\)、\(\Hat{u}_I\)、\(\Hat{u}_..\),\(n\). これらは、未知の母集団の切片\(\left(\beta_0\right)\)、傾き\(\left(\beta_1\right)\)、および誤差項\((u_i)\)の推定値です。
上に示した式は、一見するとあまり直感的ではないかもしれません。 次の対話型アプリケーションでは、OLSの仕組みを理解するのに役立つことを目的としています。 観測値を追加するには、データが点で表される座標系をクリックします。 複数の観測値が利用可能になると、アプリケーションは、OLSと右側のパネルに表示されるいくつかの統計を使用して回帰線を計算します。 左側のパネルにさらに観測値を追加すると、結果が更新されます。 ダブルクリックするとアプリケーションがリセットされ、すべてのデータが削除されます。Rで\(\hat{\beta}_0\)と\(\hat{\beta}_1\)を計算するには、多くの方法があります。 その前に、CASchoolsデータセットを添付します。
attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329attach(CASchools)を呼び出すと、CASchoolsに含まれる変数をその名前でアドレス指定することができます: データセットと組み合わせて$演算子を使用する必要はなくなりました。Rは変数名を直接評価することができます。
rは、このオブジェクトが接続されたデータベースに含まれる変数の名前を共有する場合、ユーザー環境でオブジェクトを使用します。 しかし、そのような(一見)アンビバレンスを避けるために、常に独特の名前を使用する方が良い方法です!
この章の残りの部分では、添付されたデータセットCASchoolsに含まれる変数を直接アドレスすることに注意してください!
もちろん、これらのタスクを実行するにはさらに手動の方法があります。 OLSが最も広く使用されている推定手法の1つであるため、Rには既にlm()(線形モデル)という名前の組み込み関数が含まれており、回帰分析を実行する
指定する関数の最初の引数は、plot()と同様に、基本構文y~xを使用した回帰式で、yは従属変数、xは説明変数です。 引数dataは、回帰で使用されるデータセットを決定します。 ここでは、テストの点数とクラスサイズの関係が分析される本の例を再訪します。 次のコードでは、lm()を使用して、本書の図4.3に示されている結果を複製します。
# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28推定された回帰直線をプロットに追加しましょう。 今回は、引数xlimとylimを設定することで、両方の軸の範囲を拡大します。
# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model) 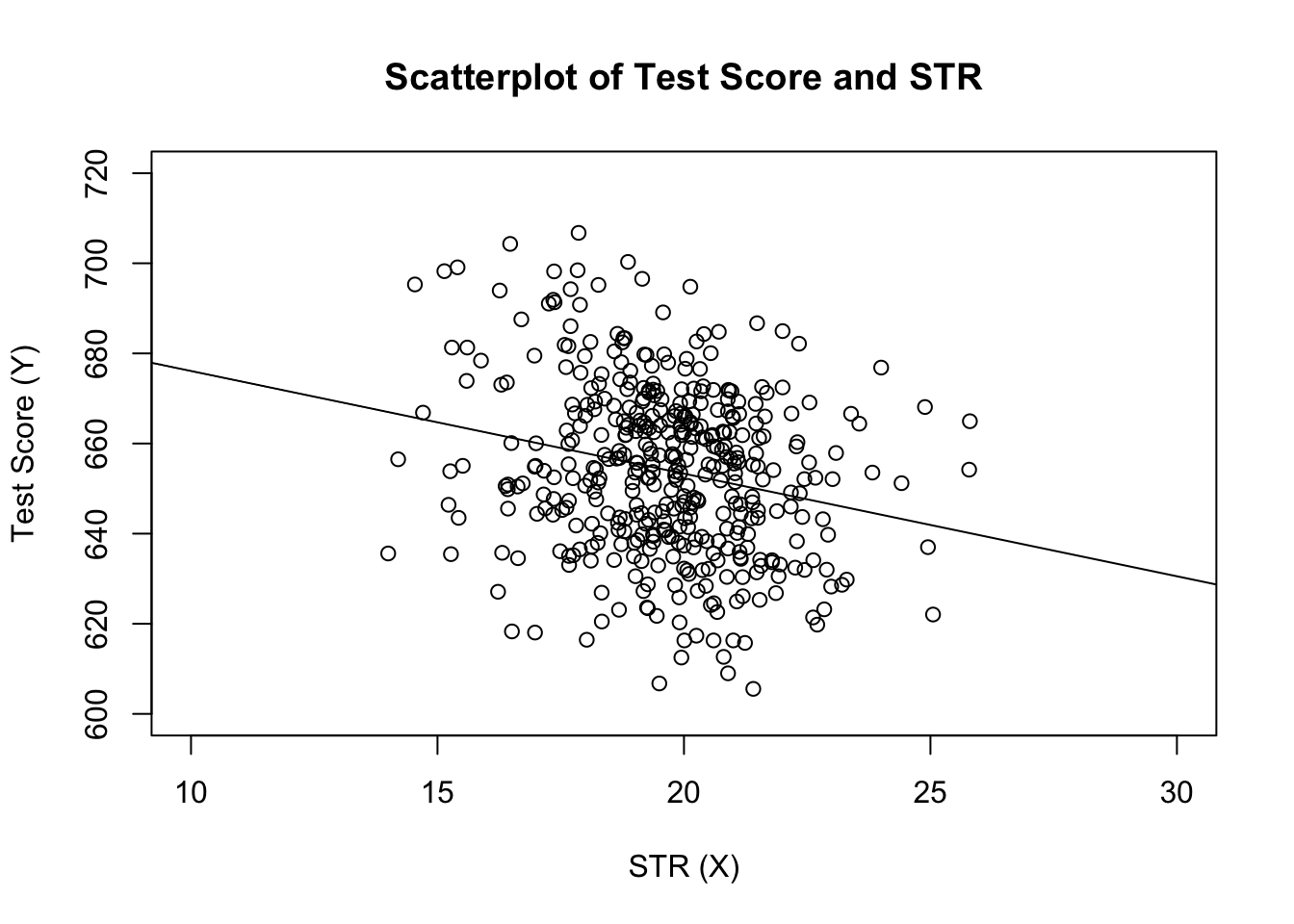
今回は、切片パラメータと勾配パラメータをablineに渡していないことに気付きましたか? 単一のリグレッサーのみを含むクラスlmのオブジェクトでabline()を呼び出すと、Rは回帰線を自動的に描画します。