仮定された知識
学生は、以前の年に幾何学との広範な非公式の経験を持っていたでしょう、これは年7-10に適切な幾何学へのより体系的なア このモジュールに関連する年F−6からの特定のトピックは次のとおりです:
- コンパスと定規の使用と幾何学的図形の慎重な描画。
- 角度の種類、少なくとも直角、鋭角、鈍角、および
反射角を含む。 - 三角形、二等辺三角形と正三角形の非公式な紹介を含む。
- 四角形、正方形、長方形、平行四辺形、台形、菱形への非公式な紹介を含む。
- 翻訳、反射、回転、拡大、
、二等辺三角形、長方形、菱形の折り畳みなどの活動の文脈における対称性を持つ非公式の経験。
 幾何学は、私たちの周りの世界をモデル化するために使用されます。 家の屋根の眺めは三角形、trapeziaおよび長方形を明らかにし、舗装および浴室のタイルパターンは六角形、五角形、三角形および正方形を使用する。
幾何学は、私たちの周りの世界をモデル化するために使用されます。 家の屋根の眺めは三角形、trapeziaおよび長方形を明らかにし、舗装および浴室のタイルパターンは六角形、五角形、三角形および正方形を使用する。
建築家、タイラー、建築家、グラフィックデザイナー、webデザイナーは、日常的に自分の仕事で幾何学的なアイデアを使用しています。 そのような幾何学的物体を分類し、その特性を研究することは非常に重要である。 幾何学はまた、芸術において多くの用途を有する。
算術は基本的な研究対象と同じように数を持っているので、点、線、円は平面幾何学の基本的な構成要素です。
中等学校の幾何学では、正確に定義するのがまったく容易ではないいくつかの直感的なアイデア(点、線、角度)から始まり、いくつかの定義(垂直に反対の角度、平行線など)が続き、これらから重要な事実を推論し、しばしば定理と呼ばれる。 中学校では、厳しさのレベルは一年から次の年にゆっくりと開発する必要がありますが、すべての段階で明確な設定は非常に重要であり、強調すべき
したがって、幾何学は、学生が人生の多くの分野でアプリケーションを持っている彼らの幾何学的直感を開発する機会を与え、また、論理的な引数を構
コンテンツ
点と線
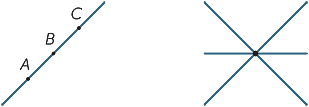
平面幾何学における最も単純なオブジェクトは点と線です。 それらは非常に単純なので、それらの正確な定義を与えることは難しいので、代わりに私たちは学生に私たちの直感に沿った特性の大まかな説明を ポイントは位置をマークしますが、サイズはありません。 実際には、点を描くとき、それは明らかに明確な幅を持っていますが、それは私たちの想像力の中の点を表しています。 線には幅がなく、両方向に無限に延びています。 私たちが線を描くとき、それは幅を持ち、端を持っているので、実際には線ではなく、私たちの想像力の中の線を表しています。 2つの異なる点AとBが与えられた場合、両方の点を通過する1つの(そして1つだけの)線があります。 ポイントと名前の行を参照するには、行上の2つのポイントを示すか、 やmのような小さな文字を使用します。
やmのような小さな文字を使用します。

二つの異なる線が与えられた場合、二つの可能性があります:それらは一点で会うか、それらがどれだけ延長されていても(または生成されていても)会うことはないかもしれません。 交わることのない線は平行線と呼ばれます。 第二の図では、AB||CDと書いています。
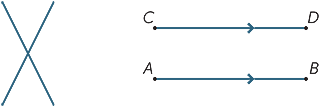
直線上にある3つ(またはそれ以上)の点を共線と呼びます。
一点で交わる三つの(またはそれ以上の)線は並行と呼ばれます。
|
|
|
| コリニア |
コンカレント |
演習1
並行していない3本の線を描き、2本の線が平行にならないようにします。
演習2
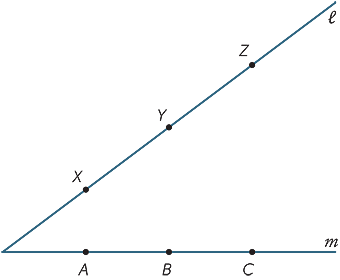
下の図の大きなコピーを作成します。 点x、Y、Zは線 上の任意の点であり、A、B、Cは線m上の任意の点です。AyとXBを結合して交点Rを呼び出します。BzとYCを結合して交点Pを呼びます。CXとZAを結合して交点Qを呼びます。点P、Q、Rについて何に気づいていますか? (この結果はパップスの定理、c.340ADと呼ばれています。)
上の任意の点であり、A、B、Cは線m上の任意の点です。AyとXBを結合して交点Rを呼び出します。BzとYCを結合して交点Pを呼びます。CXとZAを結合して交点Qを呼びます。点P、Q、Rについて何に気づいていますか? (この結果はパップスの定理、c.340ADと呼ばれています。)
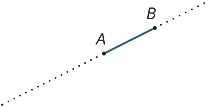 AとBを直線上の2点とする。 区間
AとBを直線上の2点とする。 区間
ABは、2つの端点を含む、AとBの間の線の一部です。
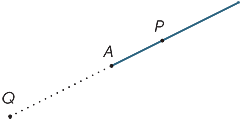 図中の点Aは、線を光線と呼ばれる2つの部分に分割しています。 光線APは、点P(および点A)を含む光線である。
図中の点Aは、線を光線と呼ばれる2つの部分に分割しています。 光線APは、点P(および点A)を含む光線である。
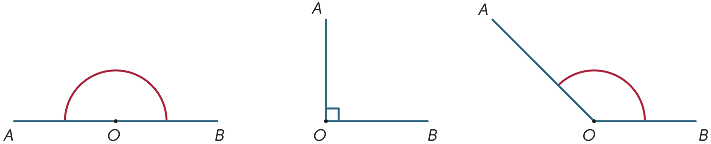
9.図では、光線OAとOBの間の影付き領域は、角度AOBまたは角度BOAと呼ばれています。 角度記号![]() が書かれているので、
が書かれているので、![]() AOBと書きます。
AOBと書きます。
 外側の影付き領域は、OAとOBによって形成される反射角と呼ばれます。 ほとんどの場合、reflexという言葉を指定しない限り、すべての角度は光線の間の領域を指し、光線の外ではありません。
外側の影付き領域は、OAとOBによって形成される反射角と呼ばれます。 ほとんどの場合、reflexという言葉を指定しない限り、すべての角度は光線の間の領域を指し、光線の外ではありません。
角度の大きさ
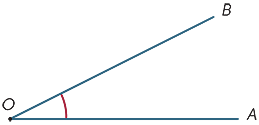 光線OBが点Oを中心に回転してOAに沿っていると想像してください。 旋回の量は、角度AOBの大きさと呼ばれます。 同様に、反射角のサイズを定義することができます。
光線OBが点Oを中心に回転してOAに沿っていると想像してください。 旋回の量は、角度AOBの大きさと呼ばれます。 同様に、反射角のサイズを定義することができます。
私たちはしばしば小さなギリシャ文字、α、β、γ、を使用します。.. 角度のサイズを表す。
一つの完全な回転に対応する角度の大きさは、(バビロニア人によって)360等分に分割され、これを度と呼んでいます。 (それは年の日数に近いので、彼らはおそらく360を選択しました。 したがって、直線の大きさは180°であり、直角の大きさは90°である。 他の角度は、分度器を使用して(およそ)測定することができる。
|
|
||
| 直線 | 直角 |
鈍角 |
角度は、そのサイズに応じて分類されます。 サイズαの角度は、0°<α<90°であれば急性
(シャープを意味する単語)であり、
90°<α<180°であれば鈍角(鈍く意味する単語)であり、180°<α<360°であれば反射であると言う。
分度器は二つのスケールを持っているので、学生は描画と
角度を測定するときに注意する必要があります。 分度器を使用して次のような角度を描画することは価値のある練習です30°, 78°, 130°, 163°.
3
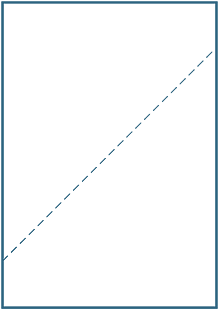 a4用紙を(斜めに)反対側の角に合わせて折ります。 形成された折り目に沿って線を描き、折り目と側面との間の角度を測定します。
a4用紙を(斜めに)反対側の角に合わせて折ります。 形成された折り目に沿って線を描き、折り目と側面との間の角度を測定します。
上記の演習では、二つの角度が一緒に直線を形成するので、180°に追加します。 180°に加えられる2つの角度は補足の角度と呼ばれます;従って45°および135°は補足の角度です。
90°に加算される2つの角度は相補的な角度と呼ばれ、23°と67°は
相補的な角度です。
点における角度
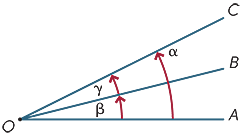 ある点における二つの角度は、それらが共通の光線を共有する場合、隣接していると言われています。 したがって、図中では、<5 0 0 8>AOBと<5 0 0 8>BOCが隣接している。
ある点における二つの角度は、それらが共通の光線を共有する場合、隣接していると言われています。 したがって、図中では、<5 0 0 8>AOBと<5 0 0 8>BOCが隣接している。
隣接する角度を加えることができるので、図中の
α=β+γ。
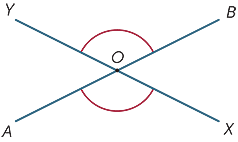
二つの線が交差すると、交点に四つの角度が形成されます。 図中の
は、![]() AOXと
AOXと![]() BOYとマークされた角度を垂直方向に反対と呼びます。
BOYとマークされた角度を垂直方向に反対と呼びます。
 以降
以降
-
 AOXは
AOXは BOX(ストレートアングル)の補足です。
BOX(ストレートアングル)の補足です。 -
 少年も
少年も 箱の補足です(直アングル),
箱の補足です(直アングル),
我々は、これらの垂直方向に反対する角度、![]() AOXと
AOXと![]() BOYは等しいと結論づけることができます。 したがって、私たちは最初の
BOYは等しいと結論づけることができます。 したがって、私たちは最初の
重要な幾何学的声明を持っています:
垂直方向の反対の角度は等しいです。
幾何学(および一般的には数学)の結果はしばしば定理と呼ばれます。 定理は、論理的控除によって証明できる重要な文です。 上の議論は定理の証明であり、定理の宣言の後に形式的に証明が提示されることがある。
 二つの線が交差して四つの角度がすべて直角である場合、線は垂直であると言われます。
二つの線が交差して四つの角度がすべて直角である場合、線は垂直であると言われます。
点における角度-幾何学的引数
幾何学的引数には、次の理由が使用できます:
- 隣接する角度を加算または減算することができます。
- 回転中の角度は360°に追加されます。
- 直線の角度は180°に追加されます。
横線と平行線
 横とは、他の2本の線と交わる線のことです。
横とは、他の2本の線と交わる線のことです。
対応する角度
さまざまな角度が横方向によって形成されます。 下の図では、2つのマークされた角度は対応する角度と呼ばれます。
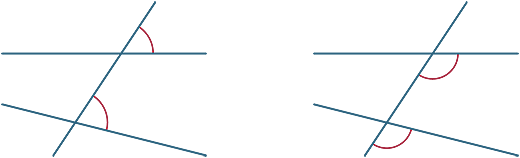
 ここでは、横方向で切断された2本の線が平行であるときに何が起こるかを見ていきます。
ここでは、横方向で切断された2本の線が平行であるときに何が起こるかを見ていきます。
最初に、角度αがβより大きい場合、CDはABをFの左に交差し、βより小さい場合、Fの右に交差します。
あるいは、角度QGDをGがFと一致するまでGFに沿って平行移動すると想像してください。 この観察は、推測に私たちをリードしています:
平行線から形成される対応する角度は等しい。
この結果を証明することはできませんが、幾何学的にもっともらしいことが示されています。 私たちはそれを幾何学の公理として受け入れます。 公理は、私たちが証明することはできませんが、直感的に合理的な声明です。 隣接する角度が追加されてもよく、2つの点が線などを決定するなど、我々がすでに述べた事実の多くがあることに注意してください。 は公理でもありますが、このように明示的に述べていません。
交互の角度
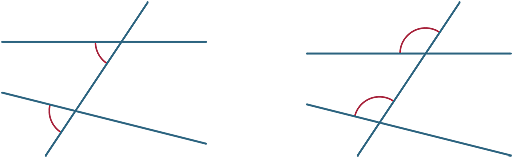
各図では、2つのマークされた角度は交互の角度と呼ばれています(横の交互の側面にあるため)。

 線ABとCDが平行である場合、交互の角度は等しくなります。 この結果は今証明することができる。
線ABとCDが平行である場合、交互の角度は等しくなります。 この結果は今証明することができる。
![]() DGQ=α(対応する角度,AB|/CD)
DGQ=α(対応する角度,AB|/CD)
![]() DGQ=β(Gで垂直に反対の角度)
DGQ=β(Gで垂直に反対の角度)
だからα=β。
要約すると、
平行線から形成される代替角度は等しい。
共内角
最後に、以下の各図では、二つのマークされた角度は共内角と呼ばれ、横の同じ側にあります。

線ABとCDが平行である場合、共内角が等しくないことは明らかですが、それらは補足的であること、すなわちそれらの合計は180°であることがわ
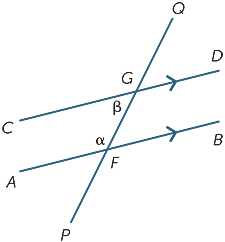 これは証明するのも簡単な結果です:
これは証明するのも簡単な結果です:
![]() BFG=β(alternate angle,AB||CD)
BFG=β(alternate angle,AB||CD)
α+β=180°(Fにおける直線角)
要約すると、
平行線から形成される共内角は補足的なものです。
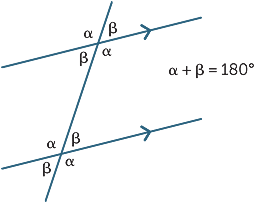 三つの結果は、次の図によって
三つの結果は、次の図によって
要約することができます:
数値例
図の角度に関する情報を考えると、上記の結果を使用して、図の他の角度の大きさ これは、多くの場合、非公式に角度追跡と呼ばれるシンプルだが非常に重要なスキルです。 問題を解決する際には、ステップの順序は必ずしも一意ではありません。 いくつかの異なるが、同様に有効なアプローチがあるかもしれません。
たとえば、次の図では、角度BACのサイズを求めます。

![]() DCA=102°(交互の角度、AC/BD)
DCA=102°(交互の角度、AC/BD)
![]() BAC=78°(共内角、AB//CD))
BAC=78°(共内角、AB//CD))
演習4
代替の一連のステップを使用して![]() BACを見つけます。
BACを見つけます。
運動5
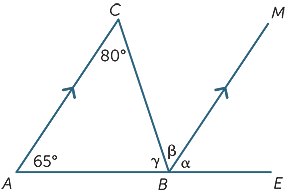 平行線のプロパティのみを使用して、次の図で欠けている角度を(理由付きで)見つけます。
平行線のプロパティのみを使用して、次の図で欠けている角度を(理由付きで)見つけます。
演習6
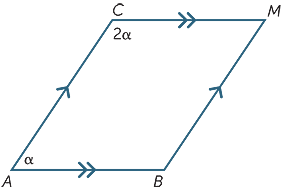
次の図でαの値を求めます。
逆の文
数学の多くの文には逆の文があり、その中で含意は反対の方向に行きます。 たとえば、ステートメント
‘は、すべての偶数で0、2、4、6、または8で終わります。’
は逆
‘0、2、4、6、または8で終わるすべての数は偶数です。’
この特定の文とその逆は両方とも真実ですが、これは決して常に
の場合ではありません。
たとえば、次の2つのステートメントは互いに逆です。
‘4の倍数はすべて偶数です。’
‘すべての偶数は4の倍数です。’
ここでは、最初の文は真ですが、2番目の文は偽です。
練習7
書き留める:
a![]() その逆も真である真の幾何学的文、
その逆も真である真の幾何学的文、
b![]() その逆も真である偽の幾何学的文、
その逆も真である偽の幾何学的文、
c![]() その逆も偽である偽の幾何学的文。
その逆も偽である偽の幾何学的文。
平行線の逆定理
平行線から形成された対応する角度が等しいことがわかりました。 逆の文は次のように書き留めることができます。
文:線が平行であれば、対応する角度は等しくなります。
コンバース: 対応する角度が等しい場合、線は平行である。
逆の文も真であり、しばしば二つの線が平行であることを証明するために使用されます。 同じことが、交互および共内角に関しても同様である。
文:線が平行であれば、代替角度は等しい。
逆:交互の角度が等しい場合、線は平行です。
声明:線が平行であれば、共内角は補足的です。
コンバース: 共内角が補助的である場合、線は平行である。
したがって、各図において、線ABとCDは平行である。

運動8
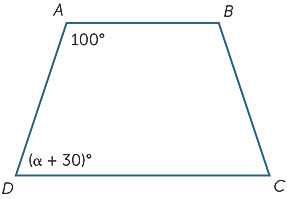 αのどの値がABをCDと平行にするのでしょうか?
αのどの値がABをCDと平行にするのでしょうか?
三つの会話の証明
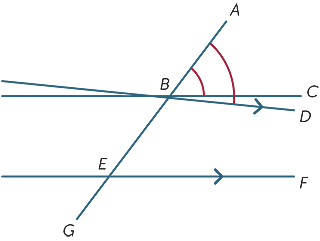 我々は、横によって形成された対応する角度が等しいと仮定し、我々は線が平行であることを示しています。図では、
我々は、横によって形成された対応する角度が等しいと仮定し、我々は線が平行であることを示しています。図では、![]() ABC=
ABC=![]() BEFと仮定します。
BEFと仮定します。
BCとEFが平行でない場合、
BDをEFと平行に描画します。BDとEFは平行であるため、![]() ABD=
ABD=![]() BEFなので、
BEFなので、![]() ABC=
ABC=![]() ABDこれは、線BCとBDが同じでない限り明らかに不可能です。 したがって、線BCとEFは平行です。
ABDこれは、線BCとBDが同じでない限り明らかに不可能です。 したがって、線BCとEFは平行です。
他の証明も同様に続く。
演習9
は、第二の逆定理(代替角度)の証明を与えます。
三角形の角度和
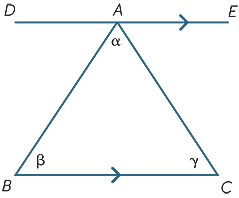 前のセクションからの結果は、幾何学における最も重要な事実の一つを推測するために使用することができます−三角形の角度の合計は180°です。
前のセクションからの結果は、幾何学における最も重要な事実の一つを推測するために使用することができます−三角形の角度の合計は180°です。
図のように、角度α、β、γを持つ三角形ABCから始めます。 BCに平行なDAE線を描きます。 その後,
![]() DAB=β(交互の角度,BC|/DE)
DAB=β(交互の角度,BC|/DE)
![]() Α+β+γ=1 8 0°(直線角)である。
Α+β+γ=1 8 0°(直線角)である。
したがって、我々は定理を証明しました
三角形の角度の合計は180°です。
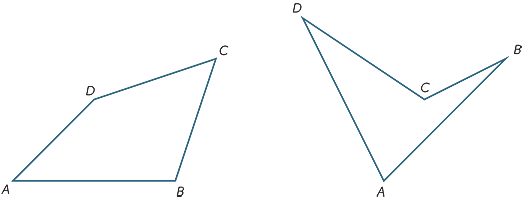
四辺形は四辺で囲まれた平面図形です。 <7751><3086><4357>練習問題10<7751><4357>四辺形ABCDを2つの三角形に分割して、角度の合計を求めます。
Links forward
このモジュールの材料は、慎重に定義されたオブジェクト、仮定される公理、および私たちが証明した定理の合理的に体系的な基礎の上に幾何学を置き始めています。 これに基づいて、我々は含む平面幾何学の体系的なアカウントを開発することができます:
- ピタゴラスの定理
- 合同と合同の三角形
- 類似と類似の三角形
- 二等辺三角形と正三角形
- 正方形、長方形、平行四辺形、菱形、台形を含む特別な四辺形
- 円の幾何学
- 円の幾何学
- 円の幾何学
- 円の幾何学
- 円の幾何学
- 円の幾何学
- 円の幾何学
- 円の幾何学
- 円の幾何学…..
平面幾何学は、数学の他の多くの分野でも基本的なものになります:
- 変換
- 三次元幾何学
- 面積と体積
- 三角法
- 座標幾何学
- 円と放物線のグラフ。
接線と領域のアイデアは、11-12年に微積分につながります。
歴史と応用
歴史
エジプトのピラミッドと巨大な寺院の信じられないほどの構造は、エジプト人が少なくとも実用的なレベルで、基本的な幾何学の非常に良い実用的な知識と理解を持っていたに違いないことを明らかにしている。 一方、彼らがその知識を正式な方法で体系化したという証拠はありません。 これは古代ギリシャ人に任されました。 私たちは、Thales(ca)という主張を除いて、その体系化の詳細な知識を持っていません。 紀元前624年-紀元前624年。 紀元前546年)は、演繹幾何学の始まりをマーク幾何学的事実の最初の”証明”を与えた。 ピタゴラスの学校はこの仕事を続け、プラトン(紀元前428年-紀元前348年)は、彼が彼の文章で幾何学的事実に言及したときに、以前の数学者の仕事に明らかに ソクラテスが一連の論理的控除によって幾何学的定理に到達するために奴隷の少年を得る彼の作品The Menoの幾何学的対話は、読む価値がある。 幾何学の起源が不明な場合、「最終生成物」はそうではありません。 アレクサンドリアで書いたユークリッド(紀元前323年-紀元前283年)は、2000年以上にわたって幾何学の標準教科書に残った要素と呼ばれる顕著な作品を生み出した。 この作品では、ユークリッドは、(そのような点や線のためのような)定義、仮定、および共通の概念の数を設定します。 (これらの日、私たちはそれらを公理と呼んでいます。)これらから、彼は論理的に、非常に慎重に選択された順序で、我々は一般的にユークリッド幾何学として参照する非常に多くの定理を開発しました。 ユークリッドの後に発見されたパップスの定理のような他の幾何学的結果の数がありますが、これらは一般的に中等学校ではカバーされていません。
ユークリッドの5つの仮定のうちの1つは、他の仮定ほど明らかに真実ではありませんでした。 Playfairの公理として知られているその1つのバージョンは、次のように述べています: 線 と点Pが与えられ、
と点Pが与えられ、 上ではなく、Pを通過する
上ではなく、Pを通過する に平行な線が1つだけあります。「これは、そのような平行線がないと仮定するか、そのような線が複数あると言うことによって行われます。 これは、非ユークリッド幾何学の開発につながり、そのうちの一つは宇宙のための良いモデルの一つを提供することが判明しました。
に平行な線が1つだけあります。「これは、そのような平行線がないと仮定するか、そのような線が複数あると言うことによって行われます。 これは、非ユークリッド幾何学の開発につながり、そのうちの一つは宇宙のための良いモデルの一つを提供することが判明しました。
アプリケーション
非常に現実的な意味では、幾何学と幾何学的直感はすべての
数学の基盤を形成します−幾何学は微積分と
すべての多くの応用につながる座標幾何学につながります−そしてカリキュラムにおいて非常に重要です。
より実用的なレベルでは、建築家、測量士、エンジニア、建築家は何世紀にもわたって幾何学と幾何学的アイデアのヘビーユーザーでした。 最近では、コンピュータの発展に伴い、グラフィックアーティストやwebデザイナーは、自分の仕事で幾何学を必要とし、使用する人々のこのグループに参加し 幾何学がいかに有用であるか最近尋ねられたとき、ジムケリー、応用科学者は言った:。.. ジオメトリは、設計、図面、およびコンピュータモデリングの重要な部分です。 それはまた頻繁に使用されます。.. 複合固体の構造およびバランスポイント(重心)に対する負荷の影響を理解する一環として、物理学およびその他の物理科学コース。 化学では、分子の幾何学を理解することは、物質の性質を理解することに関連しています。 より多くの例が存在する。 (Ask A Scientistのウェブサイトから。)
数学の歴史: イントロダクション、第3版、ビクター J.カッツ、アディソン-ウェスリー, (2008)
数学の歴史、D.E.スミス、ドーバー出版物ニューヨーク, (1958)
演習への回答
演習への回答1
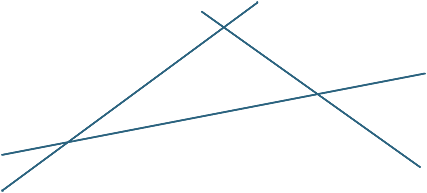
演習2
ポイントは同一直線上にあります
演習3
60°
運動4
![]() DBA=102°(対応する角度、AB||CD))
DBA=102°(対応する角度、AB||CD))
![]() Α=65°
Α=65°![]() (対応する角度、AC//BM)
(対応する角度、AC//BM)
β=80°![]() (代替角度、AC//BM)
(代替角度、AC//BM)
θ+β=115°![]() (co-section角度、AC//BM)
(co-section角度、AC//BM)
α=65°![]() (co-section角度、AC//BM)
(co-section角度、AC//BM)
β=80°![]() (co-section角度、ac//BM)
(co-section角度、ac//BM)
β=115°![]() (co-section角度、ac//BM)
(co-section角度、ac//BM)
γ+β=115°![]() (co-section角度、ac//BM)
(co-section角度、ac//BM)
内角,ac||bm)
したがって、Θ= 35°
(これは、三角形の角度合計が180°であることを証明するための構造です)
運動6
α=60°
運動7
a![]() 四辺形で、それぞれの内角を直角とする直角は長方形です。
四辺形で、それぞれの内角を直角とする直角は長方形です。
逆:長方形の各内角は直角です。
b![]() 長方形は正方形です
長方形は正方形です
逆:正方形は長方形です
c![]() 三角形の内角の角度の合計は200°です
三角形の内角の角度の合計は200°です
逆:内角の合計が200°である多角形は三角形です。
運動8
α=50°
運動9
同じ図を参照してください。
eの左にある線EF上に点Hを置きます。
![]() CBE=
CBE=![]() BEH
BEH
BCとEFが平行でない場合は、BDをEFに平行に描きます。<7751><4357>BDとEFは平行であるため、<5008>EBD=<5008>BEHとなり、線分BCとBDが同じでなければ明らかに不可能である。
したがって、線BCとEFは平行です。
10
360°
学校における数学教育の改善(タイムズ)プロジェクト2009-2011は、教育、雇用と職場関係のオーストラリア政府部門によって資金を供給されました。
ここで表明されている見解は著者のものであり、必ずしもオーストラリア政府教育雇用職場関係省の見解を表すものではありません。
©The University Of Melbourne in International Centre of Excellence for Education in Mathematics(ICE-EM),The education division of The Australian Mathematical Sciences Institute(AMSI),2010(特に明記されている場合を除く). この作品は、クリエイティブ*コモンズ表示-非営利-NoDerivs3.0Unportedライセンスの下でライセンスされています。
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()