これは、Excelスプレッドシートでk-meansクラスター分析を最初から最後まで実行する方法についてのステップバイステップガイドです。 このウェブサイトで無料でダウンロードできるクラスタ分析を自動的に実行するExcelテンプレートがあることに注意してくださ しかし、Excelでk-meansクラスタリングを自分で実行する方法を知りたい場合は、この記事を参照してください。
この記事に加えて、Excelでクラスター分析を実行する方法のビデオウォークスルーもあります。
ステップ1-データセットから始める
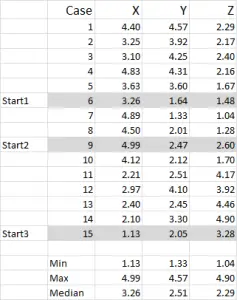
図1
この例では、x、Y、Zの3つの変数のデータがある15のケース(または回答者)を使用しています。
この例では、データが1–5にスケーリングされていることに気づ あなたのデータは、名目上のデータスケールを除いて任意の形式にすることができます(使用するデータの記事を参照してください)。
注:スケーリングされたデータを使用することを好みますが、必須ではありません。 この理由は、外れ値を「含む」ためです。 たとえば、私は所得データ(人口統計学的尺度)を使用しています–データのほとんどは約4 40,000から1 100,000かもしれませんが、私はincome5mの収入を持つ一人の人を持っています。”over250,000以上”の所得ブラケットとスケール収入1–9にその人を分類するのは簡単です-しかし、それはあなたが作業しているデータに応じてあなた次第です。
このサンプルセットから、3つの開始位置が強調表示されていることがわかります–以下のステップ3でそれらについて説明します。ステップ2–変数が2つだけの場合は、Excelで散布図を使用します
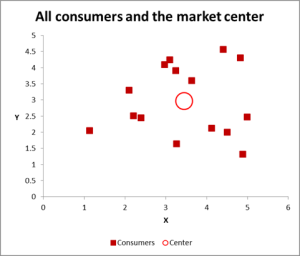
図2
このクラスター分析の例では、3つの変数を使用していますが、クラスターする変数が2つしかない場合は、散布図を開始するのに最適な方法です。 そして、時には、視覚的な手段を介してデータをクラスター化することができます。この散布図でわかるように、個々のケース(この例ではconsumerと呼んでいます)は、すべてのケース(赤い円)の平均(平均)とともにマップされています。
データ/グラフをどのように表示するかによって、いくつかのクラスターがあるように見えます。 この場合、次のグラフに示すように、3つまたは4つの比較的異なるクラスターを識別できます。
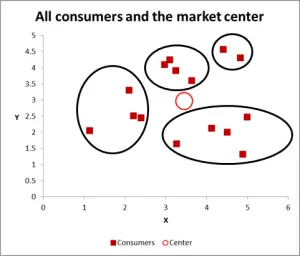
図3
この次のグラフでは、私は目に見えて可能性のあるクラスターを特定し、それらを丸で囲んでいます。 私が提案したように、考慮すべき変数が2つしかない場合の良いアプローチですが、この場合は3つの変数があります(さらに多くの変数があります)ので、この視覚的なアプローチは基本的なデータセットでのみ機能します。k–meansクラスタリングのExcel計算を行う方法を見てみましょう。
ステップThree–各データ点からクラスタの中心までの距離を計算する
このウォークスルーの例では、三つのセグメント/クラスタのみを識別すると仮定し はい、上の図では4つのクラスターが明らかですが、それは2つの変数だけを見ています。 このExcelのアプローチを使用して、好きなだけ多くのクラスターを識別できることに注意してください–以下で説明するのと同じ概念に従ってください。
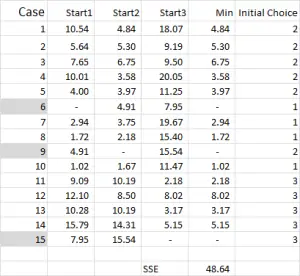
図4
k-meansクラスタリングでは、通常、分析を開始するためにいくつかのランダムなケース(開始点またはシード)を選択します。この例では、3つのクラスターを作成したいので、3つの開始点が必要です。 これらの開始点については、ケース6、9、および15を選択しましたが、任意のランダムな点も適している可能性があります。
私がこれらのケースを選択した理由は、変数Xのみを見ると、ケース6が中央値、ケース9が最大値、ケース15が最小値であったためです。 これは、これらの三つのケースが互いに多少異なっていることを示唆しているので、彼らが広がっているように良い出発点。
クラスター分析が異なる結果を生成することがある理由についての記事を参照してください。
テーブル出力を参照する–これはExcelでの最初の計算であり、クラスターの「最初の選択」を生成します。 開始1はケース6のデータであり、開始2はケース9であり、開始3はケース15です。 これらのそれぞれの共通部分は、テーブル内で0(-)を与えることに注意する必要があります。
計算はどのように機能しますか?
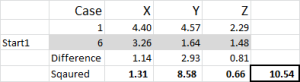
図5
ケース1、開始1=10.54–のは、テーブルの最初の番号を見てみましょう。
ケース6をクラスター1のランダムな開始点として任意に指定したことを覚えておいてください。 ここに示すように、距離を計算し、二乗和法を使用します。 セット内の3つのデータポイントのそれぞれの差を計算し、差を2乗して合計します。
ここに示すように「機械的に」行うことができます–しかし、Excelには使用する組み込みの式があります:SUMXMY2-これは使用する方がはるかに効率的です。
図4に戻ると、3つの開始点のそれぞれから各ケースの最小距離を見つけます–これは、ケースが最も近いクラスター(1、2、または3)を示します–これは”初期選択列”に示されています。
ステップ4–各クラスターセットの平均(平均)を計算する
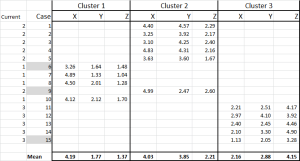
図6
これで、各ケースを最初のクラスターに割り当てました–そして、テーブル内のIF文を使用してそれをレイアウトすることができます(図6に示すように)。
表の下部には、これらの各ケースの平均(平均)があります。 N0w–1つの「代表的な」データポイントに頼るのではなく、それぞれを表す一連のケースがあります。
ステップ5–ステップ3を繰り返します–改訂された平均からの距離
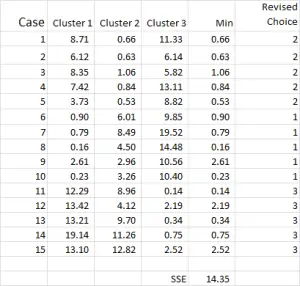
図7
クラスター解析プロセスは、クラスターが安定するまでステップ4と5(反復)を繰り返すことになりました。
各クラスターの改訂された平均を使用するたびに。 したがって、図7は2回目の反復を示していますが、今回は(図1の開始点ではなく)図6の下部で生成された平均を使用しています。
これで、クラスタアプリケーションにわずかな変更があり、ケース9–出発点の一つ–が再割り当てされていることがわかります。
下部に計算された二乗誤差の和(SSE)も表示されます。 私たちの目標は、SSEが最小限の改善しか示さず、および/または各反復でクラスター割り当ての変更が軽微になるまで、ステップ4と5を繰り返すことで
最後のステップ–クラスターをグラフ化して要約する
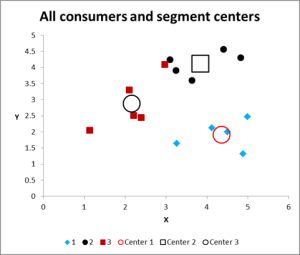
図8
複数の反復を実行した後、データをグラフ化して要約する出力が得られました。
このクラスタ分析Excelの例の出力グラフは次のとおりです。
ご覧のように、各クラスタの重心(平均)とともに、3つの異なるクラスタが示されています。
必要に応じて、このデータをExcelで作成したように、テーブル形式で提示することもできます。
クラスター3のケースを見てください–グラフの上部中央の黒い点のすぐ隣にある小さな赤い四角。 その場合は、この2つの変数チャートには表示されていない3番目の変数の影響のためにそこに座っています。