いずれかのcatamorphismはその折畳の一般化である。 カタモルフィズムは、foldを介して利用できない操作を可能にします。
この記事は、catamorphismsについての記事シリーズの一部です。 カタモルフィズムは、データ構造を潜在的によりコンパクトな値に消化する方法を記述する普遍的な抽象化です。
この記事では、どちらかのカタモルフィズム(結果とも呼ばれます)と、それを識別する方法について説明します。 この記事の冒頭では、C#のカタモルフィズムを例とともに紹介します。 この記事の残りの部分では、カタモルフィズムを推測する方法について説明します。 この記事のこの部分では、Haskellでの私の仕事を紹介します。 Haskellに慣れていない読者は、最初の部分を読むだけで、記事の残りの部分をオプションの付録と見なすことができます。
Eitherは、2つの相互に排他的な結果をモデル化するデータコンテナです。 これは、正しい(右)、または正しくない(左)のいずれかの値を返すためによく使用されます。 静的に型付けされた関数型プログラミングでは、関数全体を優先して、例外をスローするよりも成功とエラーの結果をモデル化するための、より合理的な方法を提供します。
C#catamorphism#
この記事では、いずれかのChurchエンコーディングを使用します。 いずれかのカタモルフィズムはMatchメソッドです:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
この記事まで、以前のすべてのカタモルフィズムは、初期値と関数から作られたペアでした。 どちらかのカタモルフィズムは、関数のペアであるため、一般化です。 一方の関数は左の値がある場合を処理し、もう一方の関数は右の値がある場合を処理します。 どちらの関数も同じ統一型を返す必要がありますが、これは多くの場合、ユーザーインターフェイスに表示できる文字列または類似のものです:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
左と右の両方のケースを文字列や統一的な応答タイプとして表すことができるものに変換する上記のような例がよく見られますが、これは決して必 統一型を考え出すことができれば、両方のケースをその型に変換することができます:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
上記の2つの例では、それぞれGuidとstringの値を数値に減らす2つの異なる関数を使用します。 Guidの値を数値に変換する関数は、A(10)以上の十六進数字の数をカウントします。 他の関数は、単にstringの長さを返します。 この例はほとんど意味がありませんが、Matchメソッドはそれを気にしません。
実際の使用では、どちらかがエラー処理によく使用されます。 いずれかの教会符号化に関する記事には、例が含まれています。前の記事のように、F-代数に関するBartosz Milewskiの優れた記事で説明されているように、Fixとcataを使用します。
f-代数と固定小数点は主に再帰的なデータ構造に使用されますが、非再帰的なデータ構造のF-代数を定義することもできます。 あなたはすでにBoolean catamorphismと多分catamorphismについての記事でその例を見ました。 たとえば、Maybe valuesとEitherの違いは、Eitherの両方のケースが値を運ぶことです。 これをFunctorとしてモデル化するには、いずれかに含まれる可能性のあるデータのキャリア型と2つの型引数の両方を使用します:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
私は’データ型’l(左用)とr(右用)、およびキャリアタイプc(キャリア用)を呼び出すことを選択しました。 BoolFおよびMaybeFの場合と同様に、Functorインスタンスは、キャリアタイプがLeftFケースとRightFケースの両方から欠落しているため、map関数を無視します。 BoolFとMaybeFのFunctorインスタンスのように、何も起こらないように見えますが、型レベルでは、これはまだEitherF l r cからEitherF l r c1への変換です。 関数の多くではないかもしれませんが、間違いなくendofunctorです。
MaybeとList catamorphismsを推測するときもそうであったように、HaskellはFix (EitherF l r)ような型のインスタンスを定義することにあまり満足していません。 この問題に対処するために、newtypeラッパーを導入することができます:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
次のように定義できますFunctor, Applicative, Monad, など。 ファンキーなGHC拡張機能に頼らずに、このタイプのインスタンス。 最終的には、このすべてのコードの目的は、カタモルフィズムがどのように見えるかを把握することだけです。 このコードは実際の使用を意図したものではありません。
ヘルパー関数のペアは、EitherFix値を定義することを容易にします:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
これらの関数を使用すると、EitherFix値を作成できます:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
それはあなたがカタモルフィズムを識別するために必要なすべてです。
Haskell catamorphism#
この時点で、あなたはF-代数の3つの要素のうち2つを持っています。 Endofunctor(EitherF l r)とobjectcがありますが、それでも射EitherF l r c -> cを見つける必要があります。 あなたが見つけなければならない代数は、ファンクタを’データ型’lとrではなく、そのキャリア型cに還元する関数であることに注意してください。 これに慣れるには時間がかかりますが、それはカタモルフィズムがどのように機能するかです。 しかし、これは、あなたが見るように、lとrを無視することを意味するものではありません。
前の記事と同様に、まず、次のように基づいて、カタモルフィズムになる関数を書くことから始めますcata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
これはコンパイルされていますが、undefined実装では、明らかに有用なことは何もしません。 しかし、私はそれが私が考えるのに役立つことを見つけます。 どのようにしてLeftFケースからc型の値を返すことができますか? 引数をeitherF関数に渡すことができます:技術的には、c型の引数をeitherFに渡してから、LeftFケースからその値を返すことはできますが、それはl値を無視することを意味します。
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
を使用すると、c型の引数をeitherFに渡してから、LeftFケースからその値を返すことができますが、それはl値を無視することを意味します。 これは間違っているので、代わりに引数を関数にしてlで呼び出します。 同様に、同じ方法でRightFケースを扱うことができます:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
これは動作します。 cataはFunctor f => (f a -> a) -> Fix f -> a型であるため、algはf a -> a型であることを意味します。 EitherFの場合、コンパイラはalg関数の型がEitherF l r c -> cであると推測します。
キャリアタイプcが何のためのものであるかを見ることができます。 これは代数が抽出する型であり、したがってカタモルフィズムが返す型です。
これは、どちらかのカタモルフィズムです。 これまで一貫してきたように、それはペアですが、今は2つの関数から作られています。 あなたが繰り返し見てきたように、あなたは、例えば、自明にeitherFに引数を反転することができますので、これは、唯一の可能な異形ではありません。Haskellの組み込みData.Eitherモジュールのeither関数と同型であるため、ここに示す表現を選択しました。
関数を「Either型のケース分析」と呼びます。 これらの関数(eitherFおよびeither)は、上記のC#Matchメソッドと同等です。
Basis#
eitherFを使用すると、他のほとんどの便利な機能を実装できます。 ここにBifunctorインスタンスがあります:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
そのインスタンスから、Functorインスタンスは自明に次のようになります:
instance Functor (EitherFix l) where fmap = second
Functorの上にApplicativeを追加することができます:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
<*>の実装はMaybeFixの<*>の実装に似ていることに注意してください。 同じことがMonadインスタンスの場合も同様です:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
EitherFixFoldableだけでなく、Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
興味深いことに、bifoldMapはeitherFと同一であることに注意してください。
Bifoldableインスタンスを使用すると、Foldableインスタンスを簡単に実装できます:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
bifoldMap(またはeitherF;それらは同じです)が引数として2つの関数を取るので、memptyの存在が不可解であることに気付くかもしれません。 memptyは関数ですか?
はい、memptyは関数にすることができます。 ここでは、それはあります。 任意の関数a -> mのMonoidインスタンスがあり、mはMonoidインスタンスであり、memptyはそのモノイドの恒等式です。 これがここで使用されているインスタンスです。
EitherFixがBifoldableであるのと同じように、Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
Bitraversableインスタンスに基づいてTraversableインスタンスを快適に実装できます:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
最後に、anaを使用して、標準のEither型との間の変換を実装できます。cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
これは、EitherFixがEitherと同型であることを示しており、eitherFとeitherが等価であることを再び証明しています。
リレーションシップ#
このシリーズでは、折り目を持たない構造のカタモフィズム、折り目と一致するカタモフィズム、そして今では折り目よりも一般的なカタモフィズムの様々な例を見てきました。 シリーズの紹介には、次の図が含まれています:
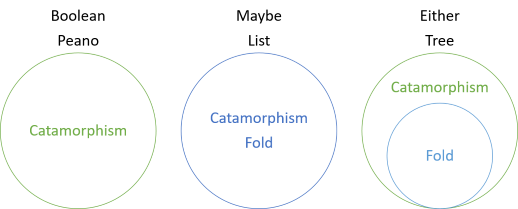
これは、ブール値とペアノ数は異形を持っていますが、折り目はありませんが、MaybeとListの場合、倍と異形は同じです。 しかし、いずれかの場合、折り畳みはカタモルフィズムの特別な場合です。 いずれかの折り目は、左側が存在しないことを”ふり”します。 代わりに、左の値は右の値が欠落していると解釈されます。 したがって、いずれかの値を折り畳むには、いずれかの値が正しい値でない場合に使用される’fallback’値を指定する必要があります:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
上記のようなGHCiセッションでは、同じタイプの2つのいずれかの値を作成できます。 右のケースはOrderingの値で、左のケースはIntegerの値です。
foldrでは、左のケースにアクセスする方法はありません。 右のOrdering値にアクセスして変換することはできますが、数値42は折畳中は無視されます。 代わりに、デフォルト値""が返されます。
これは、両方のケースにアクセスできるカタモルフィズムとは対照的です:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
このようなセッションでは、同じ値を再作成しますが、catamorphismeitherFを使用すると、左ケースと右ケースの両方にアクセスして変換できるようになりました。 言い換えれば、カタモルフィズムは、折り畳みでは不可能な操作を実行することを可能にします。
しかし、興味深いことに、折り目はカタモルフィズムの特殊化ですが、二重形はカタモルフィズムと同じであることに注意してください。
要約#
いずれかのカタモルフィズムは、関数のペアです。 一方の関数は左のケースを変換し、もう一方の関数は右のケースを変換します。 いずれかの値では、これらの関数の1つだけが使用されます。
私が最初にカタモルフィズムの概念に遭遇したとき、私はカタモルフィズムとフォールドを区別することが困難であることを発見しました。 私の問題は、私が遭遇したチュートリアルでは、主にリンクリストを使用して、その場合、折り畳みがカタモルフィズムであることを示していたと思います。 しかし、これは必ずしもそうではないことが判明しました。 カタモルフィズムは一般的な抽象化です。 折目は、一方では、私にはコレクションに大抵関連しているようである。
この記事では、倍以上のことができるカタモルフィズムの最初の例を見ました。 いずれの場合も、折畳はカタモルフィズムの特別な場合にすぎません。 しかし、あなたはまた、カタモルフィズムが二重形とどのように同一であったかを見ました。 したがって、これらの概念がどのように関連しているかはまだ完全には明らかではありません。 したがって、次の記事では、二重になっていないコンテナの例と、カタモルフィズムが実際には折り畳みの一般化であるコンテナの例を示します。
次:木のカタモルフィズム。