今日は、循環統計(方向統計と呼ばれることもあります)の簡単な紹介になります。 循環統計は、単位円の周りのベクトルとして取られた観測値を含む統計の興味深い細分です。 例として、24時間サイクルで病院で出生時間を測定したり、渡り鳥の動物のグループの方向性の分散を想像してみてください。 この種のデータは、生態学、気候学、生化学などの様々な分野に関与しています。 単位円の周りの観測値を測定する性質は、仮説検定に異なるアプローチを必要とします。 分布は、使用するために円の周りに「ラップ」する必要があり、サンプル平均やサンプル分散などの従来の推定量は水を保持しません。
この記事では、円形データセットの均一性を評価するためにRaoの間隔テストを実施します。 これは基本的な手順であり、循環データの処理の概要と考える必要があります。
はじめに
私たちは、10匹のアオウミガメの巣島への到着角からなる小さなデータセットであるカメについて仮説検定を実施します。 私たちの目標は、到着角が方向性の兆候を示すか、またはランダムな散乱をより示す場所を決定することです。
まず、circularパッケージをインストールし、turtlesデータセットを添付します。
install.packages("circular")require(circular)attach(turtles)
データのプロット
circularパッケージには独自のプロット関数plot.circularが含まれています。 カメの到着角を観察してみましょう。
plot.circular(arrival)
ここにプロットがあります: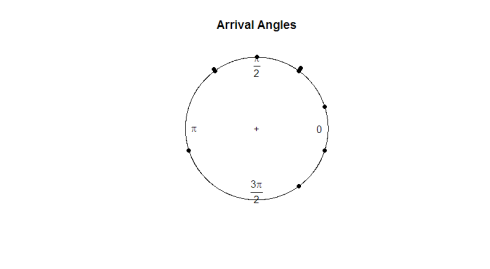
目のテストを考えると、観測値は円の周りで均一であるように見えます。 データが本当に一様であるかどうかを判断するために仮説検定を実行する場合は、角度データで機能する検定統計量を開発する必要があります。
私たちが利用するための良いパラメータは何ですか? サンプル平均を取っても、データの方向についてはあまり教えてくれません(180度は2度と358度の有用な平均ではありません)。 次のプロットでは、サンプル平均がデータの形状や広がりを表すのにどのように役に立たないかを観察します。
mean(arrival)plot.circular(mean(arrival)) 0.9120794
ここにプロットがあります: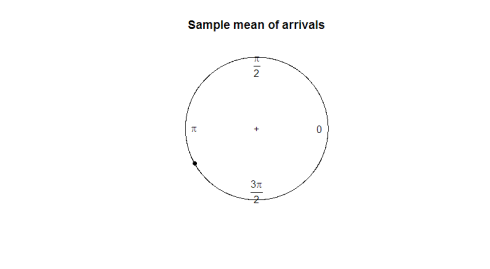
代わりに、観測間の平均空間を測定することによって方向性を決定する方法を使用します。 このテストはRaoの間隔テストと呼ばれます。
Raoの間隔テスト
Raoの間隔テストは、円形データの均一性を評価するために開発されました。 データが有意な方向性を示すかどうかを判断するために、観測間のスペースを使用します。 データが一様である場合、観測値は等間隔に配置される傾向があります。
Raoの間隔検定の検定統計量\(U\)は次のとおりです: $ $U=1/2\sum\limits_{i=1}/n|t_{i}-λ|whereここで、λ=360/n、t_{I}=f_{i+1}-f_{i}\)および\(t_{N}=(360-f_{n})+f_{n}+{1}\)
基本的に、検定統計量は連続した点間の偏差を集計し、各点はデータセット内の観測値の合計数で重み付けされます。
この仮説検定を実行するには、rao.spacing.test()関数を使用します。 私たちの帰無仮説は、データが一様分布であると言い、代替状態はデータが方向性の兆候を示しています。 テストを実行しましょう。
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
127の検定統計量が161の臨界値を下回っている場合、データはどの方向にも大きく傾くことができません。 カメの到着が一様分布であるという仮説を棄却することはできません。
結論
Raoの間隔テストは、方向性の傾向の兆候を示さないようにデータを決定しました。 一様性の帰無仮説を棄却することはできず、到着の方向に関して一様性を仮定する。 この投稿は比較的基本的なチュートリアルでしたが、データサイエンスコミュニティの多くの人々はこれまで循環データを使用していませんでした。 それはまだ進化している統計の若い分野だけでなく、に飛び込むための興味深いサブトピックです。
最後の発言
私はカリフォルニア大学サンタバーバラ校のS.Rao Jammalamadaka博士と、彼の教科書”Topics in Circular Statistics”に、循環統計の分野への関心を高めてくれたことに感謝します。