エネルギーバンド構造
半導体は、外殻原子レベルが価電子帯、”禁止”エネルギーギャップ、伝導帯からなるエネルギーバンド構造を示す結晶性材料である。
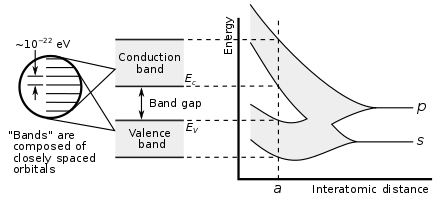
エネルギーバンドは、実際には多くの離散レベルの領域であり、連続体と見なすことができるほど密接に離間しているが、”禁止された”エネルギーギャップは、利用可能なエネルギーレベルが全くない領域である。 パウリの原理は同じ状態で複数の電子を禁止するので、外側の原子殻エネルギー準位の縮退は、互いにわずかに分離された多くの離散準位を形成する。 反対のスピンの2つの電子が同じレベルに存在する可能性があるので、結晶中に電子の対があるのと同じくらい多くのレベルがあります。 しかし、この縮退破壊は、より緊密に結合している内部原子レベルには影響しません。
最高エネルギー帯は伝導帯です。 この領域の電子は、それらの親原子から切り離され、結晶全体を自由に歩き回ることができます。 しかし,価電子帯準位の電子はより緊密に結合しており,それぞれの格子原子に関連したままである。
ギャップとバンドの幅は、原子間の格子間隔によって決まります。 これらの変数は温度および圧力にこうして依存している。 導体では、エネルギーギャップは存在しないが、絶縁体ではギャップが大きい。
常温では、絶縁体中の電子は通常すべて価電子帯にあり、熱エネルギーはこのギャップを横切って電子を励起するには不十分です。 したがって、外部電場が印加されると、結晶を通る電子の動きはなく、したがって電流はない。 一方、導体の場合、ギャップがないため、熱的に励起された電子が伝導帯に飛び込み、結晶の周りを自由に移動することが非常に容易になります。 その後、電界が印加されると電流が流れます。
半導体では、エネルギーギャップは、熱エネルギーによって伝導帯にわずかな電子しか励起されないような中間の大きさです。 したがって、電界が印加されると、小さな電流が観察される。 しかし、半導体が冷却されると、ほとんどすべての電子が価電子帯に落ち、半導体の導電率が低下する。
半導体中の電荷キャリア
0Kでは、半導体の最低エネルギー状態では、価電子帯の電子はすべて格子原子間の共有結合に関与します。
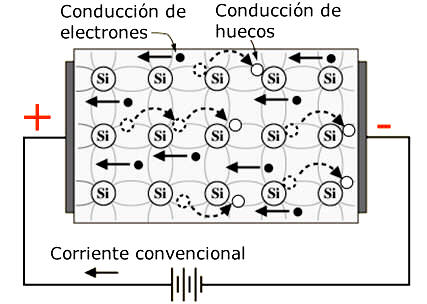
しかし、常温では、熱エネルギーの作用により価電子が伝導帯に励起され、元の位置に正孔を残すことができます。 この状態では、隣接する原子価電子がその結合から飛び降りて穴を埋めることは容易である。 これは現在、隣接する位置に穴を残します。 次の隣接する電子がシーケンスを繰り返すと、正孔は結晶を通って移動するように見えます。 正孔は価電子帯の負の電子の海に対して正であるため、正孔は正の電荷キャリアのように作用し、結晶を通るその動きも電流を構成する。
半導体では、このように二つのソースから電流が発生します: 伝導帯における自由電子の動きと価電子帯における正孔の動き。 これは、電流が電子のみによって運ばれる金属とは対照的である。
半導体に電荷を運ぶのに必要なエネルギー
媒体を横断する荷電質量粒子によって半導体中にe-h対を作るのに必要なエネルギー Wは、材料のバンドギャップエネルギー Egに依存するため、わずかではあるが温度に依存する。
この量の測定はバンドギャップエネルギーにほぼ線形依存性を示し、異なる材料について得られたデータへの線形フィットは
![]()
フォノン状態とプラズモン状態の追加励起の可能性があるため、電荷キャリア生成のエネルギーは常にバンドギャップエネルギーよりも高い。 フォノン励起はエネルギーを格子に伝達し,伝達されたエネルギーは最終的に検出器内の熱として現れる。
プラズモンは、ケイ素の平均エネルギーが17eVの価電子密度振動の量子である。 価電子はM殻の電子であり、原子に弱く結合しているだけである。 したがって、それらは高密度でほぼ均質な密度のガス、すなわち半導体材料体積中の負電荷キャリアのプラズマと考えることができる。
高エネルギー荷電粒子とX線光子を含む実験で、e-h対を作成するための平均エネルギー Wが計算され、測定されています。 シリコン中にe−h対を形成するのに必要な平均エネルギー Wは、W≦3.