Noam Chomoskyによると、文法にはタイプ0、タイプ1、タイプ2、タイプ3の4つのタイプがあります。 次の表は、それらが互いにどのように異なるかを示しています−
| 文法タイプ | 文法受け入れ | 言語受け入れ | オートマトン |
|---|---|---|---|
| タイプ0 | 無制限文法 | 再帰的に列挙可能な言語 | チューリングマシン |
| タイプ1 | 文脈依存文法 | 文脈依存言語 | 線形有界オートマトン |
| タイプ2 | 文脈自由文法 | 文脈自由言語 | プッシュダウンオートマトン |
| タイプ3 | 正規文法 | 正規言語 | 有限状態オートマトン |
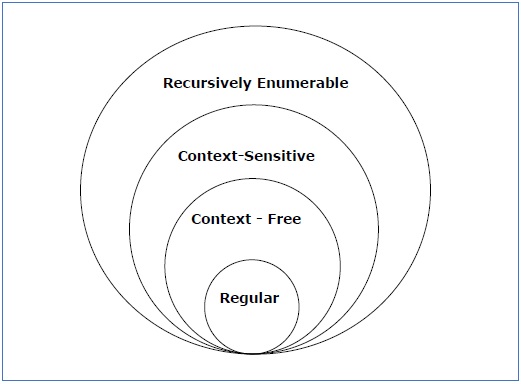
次の図を見てみましょう。 これは、文法の各タイプのスコープを示しています−
Type-3文法
type-3文法の包含は、通常の言語を生成します。 タイプ3文法は、左側に単一の非端子を持ち、右側に単一の端子または単一の端子の後に単一の非端子が続くことで構成されなければなりません。
生成は、X→aまたはX→aY
の形式でなければなりません。X,Y≤N(非端子)
およびa≤T(端子)
sがルールの右側に表示されない場合、ルールS→∞が許可されます。
例
X → ε X → a | aYY → b
タイプ2文法
タイプ2文法は文脈自由言語を生成します。
プロダクションは、a→∞
の形式でなければなりません。A≤N(非端子)
および∞(t≤N)*(端子と非端子の文字列)。
これらの文法によって生成されたこれらの言語は、非決定論的プッシュダウンオートマトンによって認識されます。
例
S → X a X → a X → aX X → abc X → ε
タイプ1文法
タイプ1文法は状況依存言語を生成します。 生成は
α a β→α≠β
の形式でなければなりません。a≤N(非端子)
とα,β,γ(t≤N)*(端子と非端子の文字列)
文字列αとβは空であってもよいが、γは空でなければならない。
ルールの右側にSが表示されない場合、ルールS→∞が許可されます。 これらの文法によって生成された言語は、線形有界オートマトンによって認識されます。
例
AB → AbBc A → bcA B → b
タイプ0文法
タイプ0文法は再帰的に列挙可能な言語を生成します。 制作には制限はありません。 それらはすべての形式文法を含む任意の位相構造文法です。
チューリングマシンによって認識される言語を生成します。
生成はα→βの形にすることができます。αは端子と非端子の文字列であり、少なくとも一つの非端子を持ち、αはnullにすることはできません。 βは端子と非端子の文字列です。
S → ACaB Bc → acB CB → DB aD → Db