評価|生物心理学|比較|認知|発達|言語|個人差|人格|哲学|社会|
方法|統計|臨床|教育|産業|専門項目|世界心理学|
統計:科学的方法·研究方法·実験デザイン·学部統計コース·統計テスト·ゲーム理論·決定理論
できれば自分でこのページを改善するのを助けてください。.
クラスター分析またはクラスタリングは、機械学習、データマイニング、パターン認識、画像解析、バイオインフォマティクスなど、多くの分野で使用されている統計データ分析のための一般的な手法です。 クラスタリングとは、類似したオブジェクトを異なるグループに分類すること、より正確にはデータセットをサブセット(クラスター)に分割することで、各サブセット内のデータが(理想的には)いくつかの共通の特性を共有すること、しばしば定義された距離尺度に従った近接性を共有することである。
データクラスタリング(または単にクラスタリング)という用語のほかに、クラスター分析、自動分類、数値分類、ボトリロジー、類型分析など、同様の意味を持つ多くの用語があります。
クラスタリングの種類
データクラスタリングアルゴリズムは、階層型または分割型にすることができます。 階層アルゴリズムは、以前に確立されたクラスターを使用して連続するクラスターを検索しますが、partitionalアルゴ 階層アルゴリズムは、凝集性(ボトムアップ)または分割性(トップダウン)にすることができます。 凝集アルゴリズムは、各要素を別々のクラスターとして開始し、それらを連続して大きなクラスターにマージします。 分割アルゴリズムは、セット全体から始まり、それを連続して小さなクラスターに分割します。
階層クラスタリング
距離メジャー
階層クラスタリングの重要なステップは、距離メジャーを選択することです。 単純な測度はマンハッタン距離であり、各変数の絶対距離の和に等しい。 名前は、2変数の場合、変数を街の通りと比較できるグリッド上にプロットすることができ、2つの点の間の距離は人が歩くブロックの数であるとい
より一般的な尺度はユークリッド距離であり、各変数間の距離の二乗を求め、二乗を合計し、その和の平方根を求めることによって計算されます。 二変数の場合、距離は三角形の斜辺の長さを見つけることに似ています。”健康心理学の研究におけるクラスター分析のレビューは、その研究分野で公開された研究の中で最も一般的な距離の尺度は、ユークリッド距離または二乗ユークリッド距離であることがわかりました。
クラスターの作成
距離測度が与えられれば、要素を組み合わせることができます。 階層クラスタリングは、クラスターの階層を構築(凝集)、または分割(分割)します。 この階層の伝統的な表現は、ツリーデータ構造(樹形図と呼ばれる)であり、一方の端に個々の要素があり、もう一方の端にすべての要素がある単一のクラスター 凝集アルゴリズムはツリーの上部から始まり、分割アルゴリズムは下部から始まります。 (図では、矢印は凝集クラスタリングを示しています。)
指定された高さでツリーを切断すると、選択された精度でクラスタリングが得られます。 次の例では、2番目の行の後に切断すると、クラスター{A}{b c}{d e}{f}が生成されます。 第三の行の後に切断すると、クラスター{a}{b c}{d e f}が生成されます。
凝集階層クラスタリング
たとえば、このデータをクラスター化するとします。 ここで、ユークリッド距離は距離計量である。
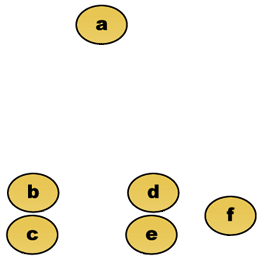
生データ
階層クラスタリング樹枝図は次のようになります:
伝統的な表現
このメソッドは、クラスターを段階的にマージすることによって、個々の要素から階層を構築します。 繰り返しになりますが、6つの要素{a}{b}{c}{d}{e}と{f}があります。 最初のステップは、クラスター内でマージする要素を決定することです。 通常、2つの最も近い要素を取りたいので、距離
二つの最も近い要素bとcをマージしたと仮定すると、次のクラスター{a}、{b、c}、{d}、{e}、{f}があり、それらをさらにマージしたいとします。 しかし、それを行うには、{a}と{b c}の間の距離を取る必要があるため、2つのクラスター間の距離を定義する必要があります。 通常、2つのクラスター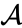
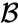
- 各クラスターの要素間の最大距離(完全リンケージクラスタリングとも呼ばれます):
- 各クラスターの要素間の最小距離(単一リンケージクラスタリングとも呼ばれます):
- 各クラスターの要素間の平均距離(平均リンケージクラスタリングとも呼ばれます):
- すべてのクラスター内分散の合計
- マージされるクラスターの分散の増加(ウォードの基準)
- 候補クラスターが同じ分布関数(V-linkage)から出現する確率)
各凝集は、以前の凝集よりもクラスタ間のより大きな距離で発生し、クラスタが発生したときにクラスタを停止することを決定することができま 離れすぎてマージできない場合(距離基準)、またはクラスターの数が十分に少ない場合(数基準)。
Partitional clustering
k-means and derivatives
K-means clustering
K-meansアルゴリズムは、中心(重心とも呼ばれる)が最も近いクラスタに各点を割り当てます。 つまり、その座標は、各次元の算術平均であり、クラスター内のすべての点について個別に計算されます。
: データセットには3つの次元があり、クラスターにはX=(x1,x2,x3)およびY=(y1,y2,y3)の2つの点があります。 このとき、重心ZはZ=(z1,z2,z3)となり、ここでz1=(x1+y1)/2およびz2=(x2+y2)/2およびz3=(x3+y3)/2となる。
アルゴリズムはおおよそ(J.マックイーン, 1967):
- ランダムにk個のクラスターを生成し、クラスターの中心を決定するか、クラスターの中心としてk個のシード点を直接生成します。
- 各点を最も近いクラスタ中心に割り当てます。
- いくつかの収束基準が満たされるまで繰り返します(通常、割り当ては変更されていません)。
このアルゴリズムの主な利点は、大規模なデータセットで実行できるシンプルさとスピードです。 その欠点は、結果のクラスターは最初のランダムな割り当てに依存するため、各実行で同じ結果が得られないことです。 これは、クラスタ間の分散を最大化します(またはクラスタ内の分散を最小化します)が、結果がグローバルな最小分散を持つことを保証しません。
QT Clust algorithm
QT(Quality Threshold)クラスタリング(Heyer et al,1999)は、遺伝子クラスタリングのために発明されたデータを分割する代替方法です。 これは、k-meansよりも多くの計算能力を必要としますが、先験的にクラスタの数を指定する必要はなく、数回実行したときに常に同じ結果を返します。
:
- ユーザーは集りのための最高の直径を選ぶ。
- クラスターの直径がしきい値を超えるまで、最も近い点、次の最も近い点などを含めて、各ポイントの候補クラスターを構築します。
- 最も多くのポイントを持つ候補クラスターを最初の真のクラスターとして保存し、クラスター内のすべてのポイントを追加の考慮から削除します。
ポイントとポイントのグループの間の距離は、完全なリンケージを使用して計算されます。 ポイントからグループの任意のメンバーまでの最大距離として(クラスター間の距離については、”凝集階層クラスタリング”のセクションを参照してくださ
Fuzzy c-means clustering
ファジィクラスタリングでは、ファジィ論理のように、各点は完全に一つのクラスターに属するのではなく、クラスターに属する程度を持ちます。 したがって、クラスタの端にある点は、クラスタの中心にある点よりも低い程度にクラスタ内にある可能性がある。 各点xに対して、k番目のクラスター

ファジィc平均では、クラスターの重心はすべての点の平均であり、クラスターに属する度合いで重み付けされている:
所属度は、クラスター
このとき、係数は正規化され、実数のパラメータ
mが2に等しい場合、これは係数を線形に正規化して合計を1にすることに相当します。 Mが1に近い場合、点に最も近いクラスタ中心には他のものよりもはるかに多くの重みが与えられ、アルゴリズムはk-meansに似ています。
ファジィc-meansアルゴリズムは、k-meansアルゴリズムと非常によく似ています:
- クラスターの数を選択します。
- クラスター内にある各点係数にランダムに割り当てます。
- アルゴリズムが収束するまで繰り返します(つまり、2回の反復間の係数の変化は、与えられた感度しきい値
以下になります)。 :
- 上記の式を使用して、各クラスターの重心を計算します。
- 各点について、上記の式を使用して、クラスタ内にある係数を計算します。
このアルゴリズムはクラスター内分散も最小化しますが、k-meansと同じ問題があり、最小値は局所最小値であり、結果は重みの初期選択に依存します。
Elbow criterion
elbow criterionは、k-meansや凝集階層クラスタリングなど、どのクラスタ数を選択すべきかを決定するための一般的な経験則です。
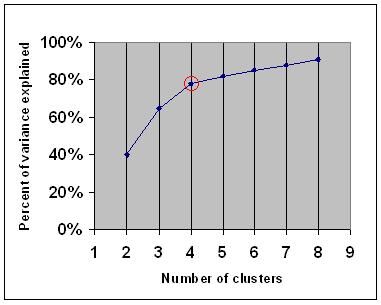
elbow criterionは、別のクラスターを追加しても十分な情報が追加されないように、いくつかのクラスターを選択する必要があると述べています。 より正確には、クラスターによって説明される分散の割合をクラスターの数に対してグラフ化すると、最初のクラスターは多くの情報を追加します(多くの分散を説明します)が、ある時点で限界利得が低下し、グラフ内の角度(エルボー)が与えられます。
次のグラフでは、肘は赤い円で示されています。 したがって、選択されたクラスターの数は4にする必要があります。
スペクトルクラスタリング
データ点の集合が与えられた場合、類似行列は行列


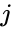
そのような手法の1つは、画像分割に一般的に使用されるShi-Malikアルゴリズムです。 これは、ラプラシアン


ここで、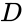
この分割は、



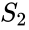
関連するアルゴリズムはMeila-Shiアルゴリズムであり、行列
応用
生物学
生物学におけるクラスタリングは、計算生物学とバイオインフォマティクスの分野で多くの応用があります。:
- トランスクリプトミクスでは、クラスタリングは関連する発現パターンを持つ遺伝子のグループを構築するために使用されます。 多くの場合、そのような基は、特定の経路のための酵素、または共調節される遺伝子などの機能的に関連するタンパク質を含む。 発現配列タグ(ESTs)またはDNAマイクロアレイを用いた高スループット実験は、ゲノミクスの一般的な側面であるゲノムアノテーションのための強力なツー
- 配列解析では、クラスタリングを使用して相同配列を遺伝子ファミリーにグループ化します。 これは、バイオインフォマティクス、および一般的な進化生物学において非常に重要な概念です。 遺伝子の重複による進化を参照してください。
マーケティングリサーチ
クラスター分析は、アンケートやテストパネルからの多変量データを扱うときに市場調査で広く使用されています。 市場研究者は、消費者の一般集団を市場セグメントに分割し、消費者/潜在的な顧客の異なるグループ間の関係をよりよく理解するために、クラスター分析
- 市場のセグメント化とターゲット市場の決定
- 製品ポジショニング
- 新製品開発
- テスト市場の選択(参照 : 実験技術)
その他のアプリケーション
ソーシャルネットワーク分析:ソーシャルネットワークの研究では、クラスタリングを使用して大規模な人々のグループ内のコミュ
画像セグメンテーション:クラスタリングを使用して、境界検出または物体認識のためにデジタル画像を別個の領域に分割することができます。
データマイニング:多くのデータマイニングアプリケーションでは、データ項目を関連するサブセットに分割する必要があります。 別の一般的なアプリケーションは、World Wide Webページなどの文書をジャンルに分割することです。
データクラスタ間の比較
二つのクラスタ間の類似性の尺度についていくつかの提案がありました。 このような尺度を使用して、一連のデータに対して異なるデータクラスタリングアルゴリズムがどの程度実行されるかを比較することができます。 これらの測度の多くは、ランド測度やFowlkes-Mallows bk測度などのマッチング行列(混同行列)から導出される。
- Jain,Murty and Flynn:データクラスタリング:レビュー,ACM Comp. サーヴ, 1999. ここで利用可能。
- 階層、k-means、ファジー c-meansの別のプレゼンテーションについては、このクラスタリングの概要を参照してください。 また、ガウスの混合についての説明もあります。
- David Dowe,Mixture Modelling page-その他のクラスタリングと混合モデルのリンク。
- クラスタリングに関するチュートリアル
- David J.C.MacKayによるオンライン教科書:Information Theory,Inference,and Learning Algorithmsには、k-means clustering、soft k-means clustering、e-M algorithmおよびe-M algorithmの変分ビューを含む派生に関する章が含まれています。
も参照してください
- k平均
- 人工ニューラルネットワーク(ANN)
- 自己組織化マップ
- 期待値最大化(EM)
参考文献
- Clatworthy,J.,Buick,D.,Hankins,M.,Weinman,J.,&Horne,R.(2005). 健康心理学におけるクラスター分析の使用と報告:レビュー。 健康心理学の英国ジャーナル10:329-358。
- Romesburg,H.Clarles,Cluster Analysis for Researchers,2004,340pp. ISBN1411606175または出版社、クリーガーパブによって出版された1990年版の復刻。 Co… 日本語訳は内田六角出版から入手可能である。 (株)エヌ-ティ-ティ、東京、日本。
- Heyer,L.J.,Kruglyak,S.and Yooseph,S.,Exploring Expression Data:Identification and Analysis of Coexpressed Genes,Genome Research9:1106-1115.
- David J.C.MacKayによるオンライン教科書:Information Theory,Inference,and Learning Algorithmsには、k-means clustering、soft k-means clustering、e-M algorithmおよびe-M algorithmの変分ビューを含む派生に関する章が含まれています。スペクトルクラスタリング用
:
- Jianbo Shi and Jitendra Malik,”Normalized Cuts and Image Segmentation”,IEEE Transactions on Pattern Analysis and Machine Intelligence,22(8),888-905,August2000. Jitendra Malikのホームページ
- Marina Meila and Jianbo Shi,”Learning Segmentation with Random Walk”,Neural Information Processing Systems,NIPS,2001. クラスター数の推定については、Jianbo Shiのホームページ
から入手できます:
- Can,F.,Ozkarahan,E.A. (1990)”テキストデータベースのカバー係数ベースのクラスタリング方法論の概念と有効性。”データベースシステム上のACMトランザクション。 15 (4) 483-517.
ソフトウェア実装
無料
- R用flexclustパッケージ
- YALE(Yet Another Learning Environment):クラスタリング用プラグインを含む知識発見とデータマイニングのための無料>クラスタリング評価のためのコンパクトな比較パッケージ(matlabでも)
- mixmod : モデルベースのクラスターと判別分析。 C++でのコード,MatlabとScilabとのインターフェイス
- LingPipeクラスタリングチュートリアルlingpipeを使用して完全およびシングルリンククラスタリングを行うためのチュート
- Weka:Wekaには、データの前処理、分類、回帰、クラスタリング、関連ルール、および可視化のためのツールが含まれています。 また、新しい機械学習スキームの開発にも適しています。