Il catamorphism per O è una generalizzazione della sua piega. Il catamorfismo consente operazioni non disponibili tramite fold.
Questo articolo fa parte di una serie di articoli sui catamorfismi. Un catamorfismo è un’astrazione universale che descrive come digerire una struttura di dati in un valore potenzialmente più compatto.
Questo articolo presenta il catamorfismo per Entrambi (noto anche come Risultato), nonché come identificarlo. L’inizio di questo articolo presenta il catamorfismo in c#, con esempi. Il resto dell’articolo descrive come dedurre il catamorfismo. Questa parte dell’articolo presenta il mio lavoro in Haskell. I lettori non confortevole con Haskell può solo leggere la prima parte, e considerare il resto dell’articolo come un’appendice opzionale.
O è un contenitore di dati che modella due risultati che si escludono a vicenda. Viene spesso utilizzato per restituire valori che possono essere corretti (a destra) o errati (a sinistra). Nella programmazione funzionale tipizzata staticamente con una preferenza per le funzioni totali, O offre un modo più sano e più ragionevole per modellare i risultati di successo e di errore rispetto alle eccezioni di lancio.
C# catamorphism #
Questo articolo utilizza la codifica Church di Entrambi. Il catamorfismo per entrambi è il metodo Match :
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
Fino a questo articolo, tutti i catamorfismi precedenti erano una coppia composta da un valore iniziale e una funzione. Il catamorfismo è una generalizzazione, poiché è una coppia di funzioni. Una funzione gestisce il caso in cui c’è un valore sinistro e l’altra funzione gestisce il caso in cui c’è un valore giusto. Entrambe le funzioni devono restituire lo stesso tipo unificante, che spesso è una stringa o qualcosa di simile che può essere mostrato in un’interfaccia utente:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
Vedrai spesso esempi come il precedente che trasforma entrambi i casi sinistro e destro in stringhe o qualcosa che può essere rappresentato come un tipo di risposta unificante, ma questo non è in alcun modo richiesto. Se riesci a trovare un tipo unificante, puoi convertire entrambi i casi in quel tipo:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
Nei due esempi precedenti, si utilizzano due funzioni diverse che riducono rispettivamente i valori Guid e string a un numero. La funzione che trasforma i valori Guid in un numero conta quante cifre esadecimali sono maggiori o uguali a (10). L’altra funzione restituisce semplicemente la lunghezza di string, se è lì. Questo esempio ha poco senso, ma il metodo Match non si preoccupa di questo.
Nell’uso pratico, O viene spesso utilizzato per la gestione degli errori. L’articolo sulla codifica della Chiesa di Entrambi contiene un esempio.
O F-Algebra #
Come nell’articolo precedente, userò Fix e cata come spiegato nell’eccellente articolo di Bartosz Milewski sulle F-Algebre.
Mentre le F-Algebre e i punti fissi sono utilizzati principalmente per strutture di dati ricorsive, è anche possibile definire un’F-Algebra per una struttura di dati non ricorsiva. Ne hai già visto un esempio negli articoli sul catamorfismo booleano e forse sul catamorfismo. La differenza tra ad esempio Maybe values e O è che entrambi i casi di Entrambi portano un valore. È possibile modellarlo come Functor con un tipo di supporto e due argomenti di tipo per i dati che possono contenere:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
Ho scelto di chiamare i’ tipi di dati ‘ l (per sinistra) e r (per destra) e il tipo di supporto c (per il supporto). Come nel caso di BoolF e MaybeF, l’istanza Functor ignora la funzione map perché il tipo di vettore manca sia nel caso LeftF che nel caso RightF. Come le istanze Functor per BoolF e MaybeF, sembrerebbe che non accada nulla, ma a livello di tipo, questa è ancora una traduzione da EitherF l r ca EitherF l r c1. Non molto di una funzione, forse, ma sicuramente un endofunctor.
Come nel caso di dedurre i catamorfismi Maybe e List, Haskell non è troppo felice di definire istanze per un tipo come Fix (EitherF l r). Per risolvere questo problema, è possibile introdurre un wrapper newtype :
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
È possibile definire Functor, Applicative, Monad, ecc. istanze per questo tipo senza ricorrere a estensioni GHC funky. Tieni presente che in definitiva, lo scopo di tutto questo codice è solo quello di capire come appare il catamorfismo. Questo codice non è destinato all’uso effettivo.
Una coppia di funzioni di supporto semplifica la definizione dei valori EitherFix :
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
Con queste funzioni, è possibile creare valori EitherFix :
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
Questo è tutto ciò che serve per identificare il catamorfismo.
Haskell catamorphism #
A questo punto, hai due su tre elementi di una F-Algebra. Hai un endofunctor (EitherF l r) e un oggetto c, ma devi ancora trovare un morfismo EitherF l r c -> c. Si noti che l’algebra che si deve trovare è la funzione che riduce il funtore al suo tipo portante c, non i ‘tipi di dati’ l e r. Questo richiede un po ‘ di tempo per abituarsi, ma è così che funzionano i catamorfismi. Questo non significa, tuttavia, che puoi ignorare l e r, come vedrai.
Come negli articoli precedenti, inizia scrivendo una funzione che diventerà il catamorfismo, basata su cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
Mentre questo compila, con le sue implementazioni undefined, ovviamente non fa nulla di utile. Trovo, tuttavia, che mi aiuta a pensare. Come è possibile restituire un valore del tipo c dal caso LeftF? È possibile passare un argomento alla funzione eitherF :
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
Mentre è possibile, tecnicamente, passare un argomento del tipo c a eitherF e quindi restituire quel valore dal caso LeftF, ciò significherebbe ignorare il valore l. Questo non sarebbe corretto, quindi, invece, rendere l’argomento una funzione e chiamarlo con l. Allo stesso modo, puoi gestire il caso RightF allo stesso modo:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
Funziona. Poiché cata ha il tipo Functor f => (f a -> a) -> Fix f -> a, ciò significa che algha il tipo f a -> a. Nel caso di EitherF, il compilatore deduce che la funzione alg ha il tipo EitherF l r c -> c, che è proprio quello di cui hai bisogno!
Ora puoi vedere a cosa serve il tipo di supporto c. È il tipo che l’algebra estrae, e quindi il tipo che il catamorfismo restituisce.
Questo, quindi, è il catamorfismo per entrambi. Come è stato coerente finora, è una coppia, ma ora fatta da due funzioni. Come hai visto ripetutamente, questo non è l’unico catamorfismo possibile, dal momento che puoi, ad esempio, capovolgere banalmente gli argomenti a eitherF.
Ho scelto la rappresentazione mostrata qui perché è isomorfa alla funzione either dal modulo incorporato Data.Either di Haskell, che chiama la funzione “Analisi dei casi per il tipo Either“. Entrambe queste funzioni (eitherF e either) sono equivalenti al metodo C# Match sopra.
Basis #
È possibile implementare la maggior parte delle altre funzionalità utili con eitherF. Ecco l’istanza Bifunctor :
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
Da quell’istanza, l’istanza Functor segue banalmente:
instance Functor (EitherFix l) where fmap = second
In cima a Functor puoi aggiungere Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Si noti che l’implementazione <*> è simile all’implementazione <*> per MaybeFix. Lo stesso vale per l’istanza Monad :
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
Non solo è EitherFix Foldable, è Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
Si noti, è interessante notare, che bifoldMap è identico a eitherF.
L’istanza Bifoldable consente di implementare banalmente l’istanza Foldable :
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
Potresti trovare la presenza di mempty sconcertante, poiché bifoldMap (o eitherF; sono identici) prende come argomenti due funzioni. mempty è una funzione?
Sì, mempty può essere una funzione. Eccolo qui. Esiste un’istanza Monoid per qualsiasi funzione a -> m, dove m è un’istanza Monoid e mempty è l’identità per quel monoid. Questa è l’istanza in uso qui.
come EitherFix è Bifoldable, è anche Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
Si può comodamente implementare il Traversable istanza basata sui Bitraversable istanza:
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
Infine, è possibile implementare le conversioni da e per la serie Either tipo, utilizzando ana come il doppio di cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
Questo dimostra che EitherFix è isomorfi a Either, che a sua volta stabilisce che eitherF e either sono equivalenti.
Relazioni #
In questa serie, hai visto vari esempi di catamorfismi di strutture che non hanno pieghe, catamorfismi che coincidono con le pieghe e ora un catamorfismo che è più generale della piega. L’introduzione alla serie includeva questo diagramma:
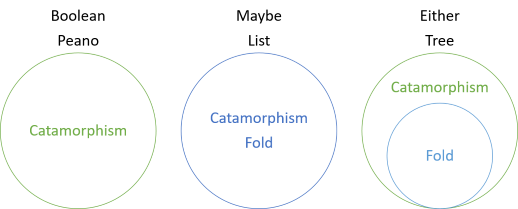
Questo mostra che i valori booleani e i numeri di Peano hanno catamorfismi, ma nessuna piega, mentre per Maybe e List, la piega e il catamorfismo sono gli stessi. Per entrambi, tuttavia, la piega è un caso speciale del catamorfismo. La piega per entrambi ‘finge’ che il lato sinistro non esiste. Invece, il valore sinistro viene interpretato come un valore destro mancante. Pertanto, per piegare entrambi i valori, è necessario fornire un valore di “fallback” che verrà utilizzato nel caso in cui uno dei due valori non sia un valore corretto:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
In una sessione GHCi come la precedente, è possibile creare due valori dello stesso tipo. Il caso destro è un valore Ordering, mentre il caso sinistro è un valore Integer.
Con foldr, non c’è modo di accedere al caso sinistro. Mentre è possibile accedere e trasformare il valore Ordering giusto, il numero 42 viene semplicemente ignorato durante la piega. Viene invece restituito il valore predefinito "".
Contrasta questo con il catamorfismo, che può accedere a entrambi i casi:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
In una sessione come questa, si ricreano gli stessi valori, ma utilizzando il catamorfismo eitherF, è ora possibile accedere e trasformare sia i casi sinistro che destro. In altre parole, il catamorfismo consente di eseguire operazioni non possibili con la piega.
È interessante notare, tuttavia, che mentre la piega è una specializzazione del catamorfismo, la bifold è identica al catamorfismo.
Sommario #
Il catamorfismo per entrambi è una coppia di funzioni. Una funzione trasforma il caso sinistro, mentre l’altra funzione trasforma il caso destro. Per qualsiasi valore, verrà utilizzata solo una di queste funzioni.
Quando ho incontrato originariamente il concetto di catamorfismo, ho trovato difficile distinguere tra catamorfismo e fold. Il mio problema era, penso, che i tutorial in cui mi sono imbattuto utilizzavano principalmente elenchi collegati per dimostrare come, in tal caso, la piega sia il catamorfismo. Si scopre, tuttavia, che questo non è sempre il caso. Un catamorfismo è un’astrazione generale. Una piega, d’altra parte, mi sembra essere per lo più legata alle collezioni.
In questo articolo hai visto il primo esempio di un catamorfismo che può fare più della piega. Per entrambi, la piega è solo un caso speciale del catamorfismo. Hai anche visto, tuttavia, come il catamorfismo fosse identico al bifold. Quindi, non è ancora del tutto chiaro come questi concetti si relazionano. Pertanto, nel prossimo articolo, si otterrà un esempio di un contenitore dove non c’è bifold, e dove il catamorfismo è, infatti, una generalizzazione della piega.
Successivo: Albero catamorfismo.