4.2 Stima dei Coefficienti del Modello di Regressione Lineare

In pratica, l’intercetta $\beta_0$ e la pista $\beta_1$ della popolazione retta di regressione sono sconosciuti. Pertanto, dobbiamo utilizzare i dati per stimare entrambi i parametri sconosciuti. Di seguito, verrà utilizzato un esempio del mondo reale per dimostrare come questo è raggiunto. Vogliamo mettere in relazione i punteggi dei test con i rapporti studente-insegnante misurati nelle scuole californiane. Il punteggio del test è la media a livello di distretto di lettura e matematica punteggi per quinta elementare. Anche in questo caso, la dimensione della classe viene misurata come il numero di studenti diviso per il numero di insegnanti (il rapporto studente-insegnante). Per quanto riguarda i dati, il California School data set (CASchools) viene fornito con un pacchetto R chiamato AER, acronimo di Applied Econometrics with R (Kleiber and Zeileis 2020). Dopo aver installato il pacchetto con install.pacchetti (“AER”) e collegandolo con la libreria(AER) il set di dati può essere caricato utilizzando la funzione data ().

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

Una volta che un pacchetto è stato installato è disponibile per l’uso in altre occasioni quando invocato con library() — non c’è bisogno di eseguire install.pacchetti () di nuovo!

È interessante sapere che tipo di oggetto abbiamo a che fare.class () restituisce la classe di un oggetto. A seconda della classe di un oggetto alcune funzioni (ad esempio plot () e summary ()) si comportano in modo diverso.

Controlliamo la classe dell’oggetto CASchools.

class(CASchools)#> "data.frame"

Si scopre che CASchools è di dati di classe.frame che è un formato conveniente per lavorare con, soprattutto per l’esecuzione di analisi di regressione.

Con l’aiuto di head () otteniamo una prima panoramica dei nostri dati. Questa funzione mostra solo le prime 6 righe del set di dati che impedisce un’uscita della console sovraffollata.

Premere ctrl + L per cancellare la console. Questo comando elimina qualsiasi codice digitato ed eseguito dall’utente o stampato nella console dalle funzioni R. La buona notizia è che qualsiasi altra cosa è lasciata intatta. Non perdete variabili definite ecc. né la storia del codice. È ancora possibile richiamare i comandi R eseguiti in precedenza utilizzando i tasti su e giù. Se stai lavorando in RStudio, premi ctrl + Su sulla tastiera (CMD + Su su un Mac) per rivedere un elenco di comandi inseriti in precedenza.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

Troviamo che il set di dati è costituito da molte variabili e che la maggior parte di esse sono numeriche.

A proposito: un’alternativa a class() e head() è str() che viene dedotta da ‘structure’ e fornisce una panoramica completa dell’oggetto. Provi!

Tornando a CASchools, le due variabili a cui siamo interessati (cioè, il punteggio di prova medio e il rapporto di studente-insegnante) non sono inclusi. Tuttavia, è possibile calcolare entrambi dai dati forniti. Per ottenere i rapporti studente-insegnante, dividiamo semplicemente il numero di studenti per il numero di insegnanti. Il punteggio medio del test è la media aritmetica del punteggio del test per la lettura e il punteggio del test di matematica. Il prossimo blocco di codice mostra come le due variabili possono essere costruite come vettori e come vengono aggiunte a CASchools.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

Se corressimo di nuovo head (CASchools) troveremmo le due variabili di interesse come colonne aggiuntive denominate STR e score (controlla questo!).

La tabella 4.1 del libro di testo riassume la distribuzione dei punteggi dei test e dei rapporti studente-insegnante. Ci sono diverse funzioni che possono essere utilizzate per produrre risultati simili, ad esempio,

media () () calcola la media aritmetica dei numeri),
sd () () calcola la deviazione standard del campione),
quantile() (restituisce un vettore specificato campione quantili per i dati).

Il prossimo blocco di codice mostra come raggiungere questo obiettivo. In primo luogo, calcoliamo le statistiche di riepilogo sulle colonne STR e punteggio di CASchools. Al fine di ottenere un buon output raccogliamo le misure in un dato.frame denominato DistributionSummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

Per quanto riguarda i dati di esempio, usiamo plot (). Questo ci permette di rilevare le caratteristiche dei nostri dati, come valori anomali che sono più difficili da scoprire guardando semplici numeri. Questa volta aggiungiamo alcuni argomenti aggiuntivi alla chiamata di plot ().

Il primo argomento nella nostra chiamata di plot(), score ~ STR, è di nuovo una formula che afferma variabili sull’asse y e sull’asse x. Tuttavia, questa volta le due variabili non vengono salvate in vettori separati ma sono colonne di CASchools. Pertanto, R non li troverebbe senza che i dati dell’argomento siano specificati correttamente. i dati devono essere conformi al nome dei dati.frame a cui appartengono le variabili, in questo caso CASchools. Ulteriori argomenti vengono utilizzati per modificare l’aspetto della trama: mentre main aggiunge un titolo, xlab e ylab aggiungono etichette personalizzate a entrambi gli assi.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")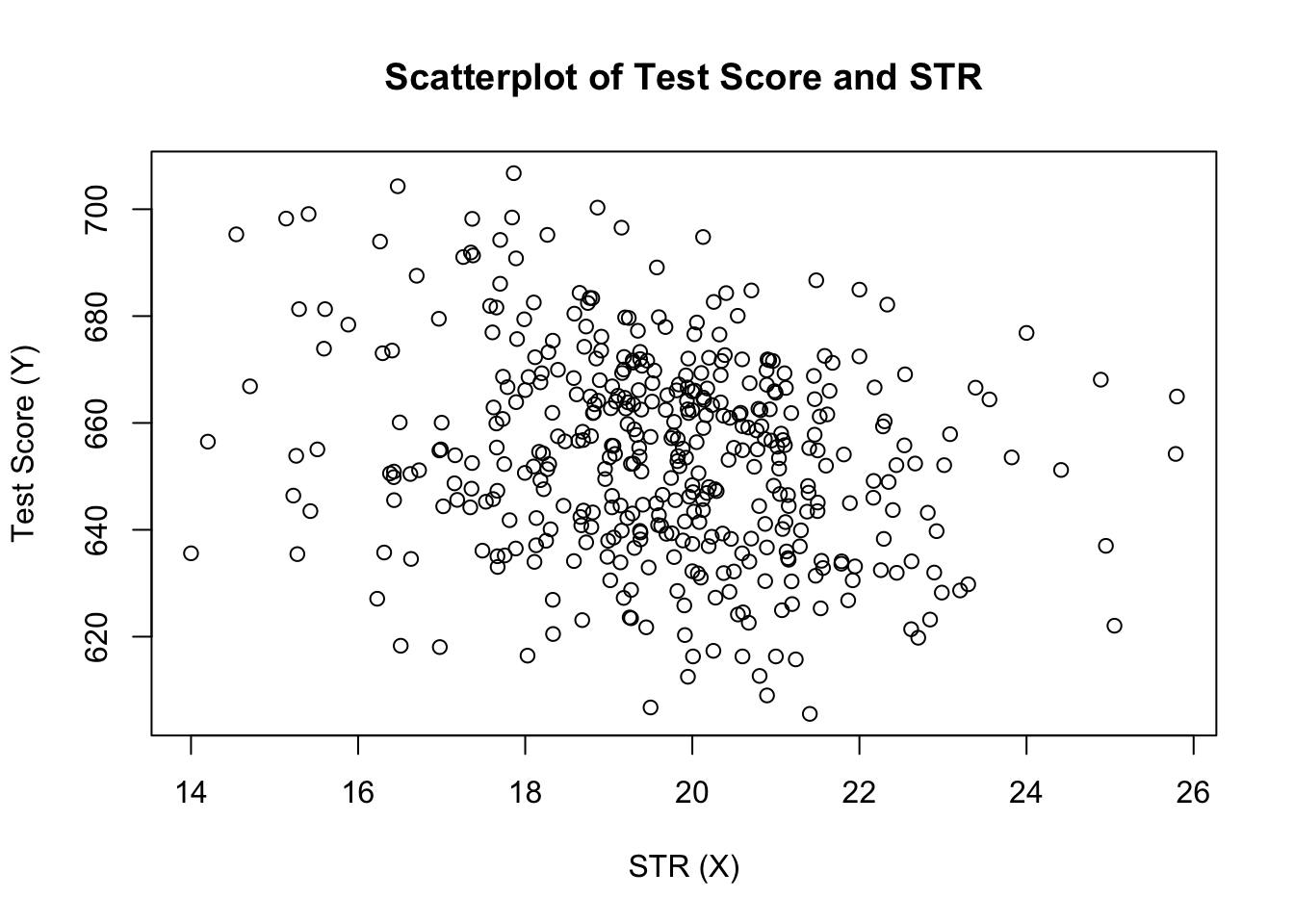

La trama (Figura 4.2 nel libro) mostra la trama a dispersione di tutte le osservazioni sul rapporto studente-insegnante e sul punteggio del test. Vediamo che i punti sono fortemente sparsi e che le variabili sono correlate negativamente. Cioè, ci aspettiamo di osservare punteggi dei test più bassi nelle classi più grandi.

La funzione cor () (vedi ?cor per ulteriori informazioni) può essere utilizzato per calcolare la correlazione tra due vettori numerici.

cor(CASchools$STR, CASchools$score)#> -0.2263627

Come suggerisce già il grafico a dispersione, la correlazione è negativa ma piuttosto debole.

Il compito che stiamo affrontando è trovare una linea che si adatti meglio ai dati. Naturalmente potremmo semplicemente attaccare con ispezione grafica e analisi di correlazione e quindi selezionare la migliore linea di montaggio eyeballing. Tuttavia, questo sarebbe piuttosto soggettivo: diversi osservatori trarrebbero diverse linee di regressione. Per questo motivo, siamo interessati a tecniche meno arbitrarie. Tale tecnica è data dalla stima dei minimi quadrati ordinari (OLS).

Lo stimatore dei minimi quadrati ordinari

Lo stimatore OLS sceglie i coefficienti di regressione in modo tale che la linea di regressione stimata sia il più “vicina” possibile ai punti dati osservati. Qui, la vicinanza è misurata dalla somma degli errori al quadrato fatti nel predire\ (Y\) dato \ (X\). Sia $b_0$ e $b_1$ alcuni stimatori di\ (\beta_0\) e$\beta_1$. Quindi la somma degli errori di stima al quadrato può essere espressa come

Lo stimatore OLS nel modello di regressione semplice è la coppia di stimatori per intercept e slope che minimizza l’espressione sopra. La derivazione degli stimatori OLS per entrambi i parametri è presentata nell’appendice 4.1 del libro. I risultati sono riassunti nel Concetto chiave 4.2.

Lo Stimatore OLS, i Valori previsti, e Residui

stimatori OLS del pendio $\beta_1$ e l’intercetta $\beta_0$ in un semplice modello di regressione lineare sono\OLS predetto valori di $\widehat{Y}_i$ e residui di $\hat{u}_i$ per\

La stima di intercettare $\hat{\beta}_0$, la pendenza del parametro $\hat{\beta}di 1$ e i residui di $\left(\hat{u}_i\right)$ sono calcolati su un campione di $n$ osservazioni di $X_i$ e $Y_i$, $i$, $…$, $e$. Queste sono stime della popolazione sconosciuta intercept $\left (\beta_0 \ right)$, slope $\left (\beta_1\ right)$ e error term$(u_i)$.

Le formule presentate sopra potrebbero non essere molto intuitive a prima vista. La seguente applicazione interattiva ha lo scopo di aiutare a capire la meccanica di OLS. È possibile aggiungere osservazioni facendo clic nel sistema di coordinate in cui i dati sono rappresentati da punti. Una volta disponibili due o più osservazioni, l’applicazione calcola una linea di regressione utilizzando OLS e alcune statistiche che vengono visualizzate nel pannello di destra. I risultati vengono aggiornati quando si aggiungono ulteriori osservazioni al pannello di sinistra. Un doppio clic ripristina l’applicazione, ovvero tutti i dati vengono rimossi.

Ci sono molti modi possibili per calcolare $\hat{\beta}_0$ e $\hat{\beta}_1$ in R. Ad esempio, potremmo implementare le formule presentate in Key Concept 4.2 con due delle funzioni più basilari di R: mean() e sum(). Prima di farlo alleghiamo il set di dati CASchools.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

Chiamare attach (CASchools) ci consente di indirizzare una variabile contenuta in CASchools con il suo nome: non è più necessario utilizzare l’operatore $ insieme al set di dati: R può valutare direttamente il nome della variabile.

R utilizza l’oggetto nell’ambiente utente se questo oggetto condivide il nome della variabile contenuta in un database allegato. Tuttavia, è una pratica migliore usare sempre nomi distintivi per evitare tali (apparentemente) ambivalenze!

Si noti che indirizziamo le variabili contenute nel set di dati allegato CASchools direttamente per il resto di questo capitolo!

Naturalmente, ci sono ancora più modi manuali per eseguire queste attività. Poiché OLS è una delle tecniche di stima più utilizzate, R ovviamente contiene già una funzione integrata denominata lm () (modello lineare) che può essere utilizzata per eseguire l’analisi di regressione.

Il primo argomento della funzione da specificare è, simile a plot(), la formula di regressione con la sintassi di base y ~ x dove y è la variabile dipendente e x la variabile esplicativa. I dati argomento determina il set di dati da utilizzare nella regressione. Ora rivisitiamo l’esempio del libro in cui viene analizzata la relazione tra i punteggi dei test e le dimensioni delle classi. Il seguente codice utilizza lm () per replicare i risultati presentati nella figura 4.3 del libro.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

Aggiungiamo la linea di regressione stimata alla trama. Questa volta ingrandiamo anche gli intervalli di entrambi gli assi impostando gli argomenti xlim e ylim.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)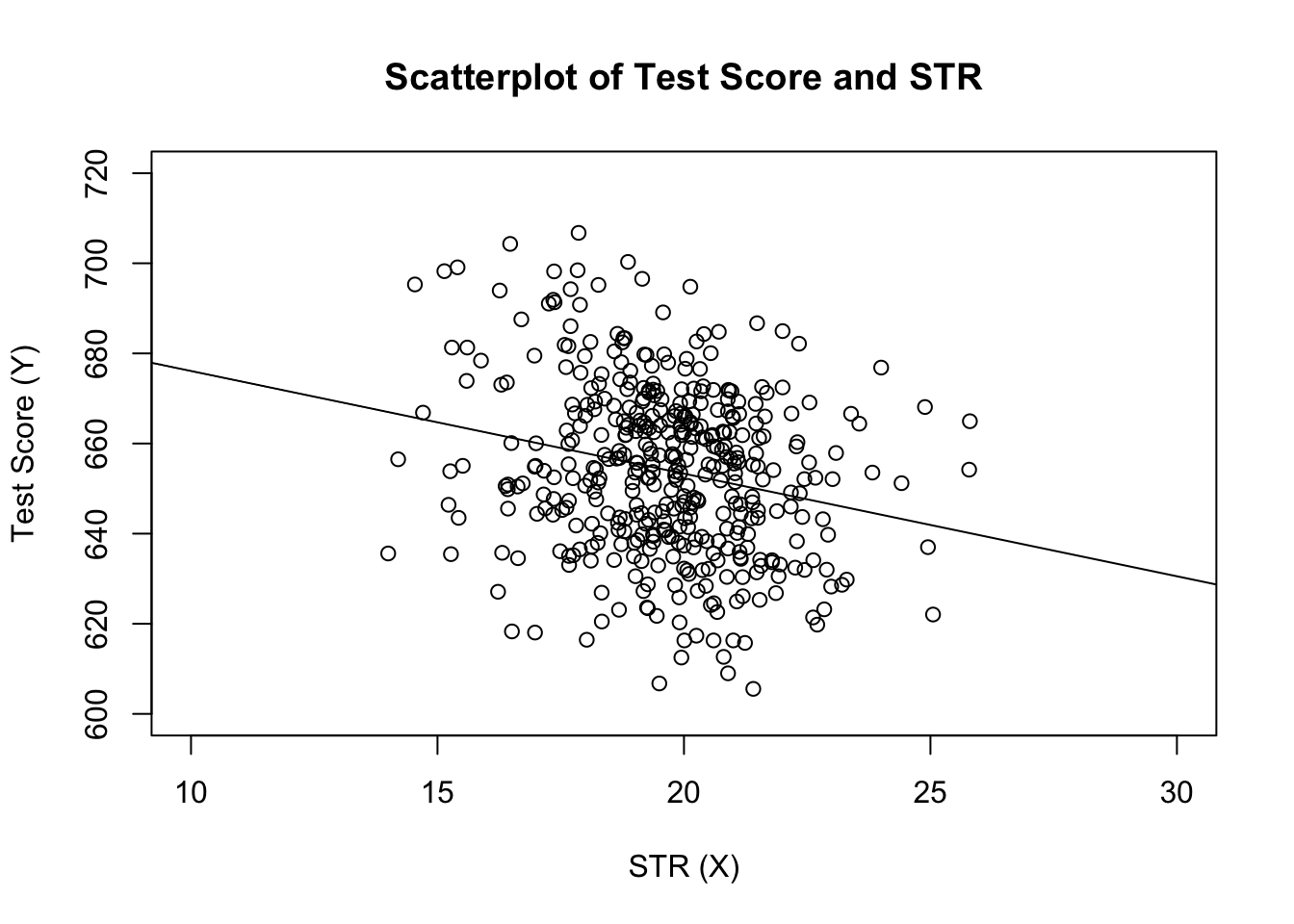

Hai notato che questa volta non abbiamo passato i parametri di intercettazione e pendenza a abline? Se si chiama abline() su un oggetto di classe lm che contiene solo un singolo regressore, R disegna automaticamente la linea di regressione!

Introduzione all’Econometria con R