Oggi sarà una breve introduzione alle statistiche circolari (a volte indicato come statistiche direzionali). La statistica circolare è un’interessante suddivisione di statistiche che coinvolgono osservazioni prese come vettori attorno a un cerchio unitario. Ad esempio, immagina di misurare i tempi di nascita in un ospedale su un ciclo di 24 ore o la dispersione direzionale di un gruppo di animali migratori. Questo tipo di dati è coinvolto in una varietà di campi, come l’ecologia, la climatologia e la biochimica. La natura delle osservazioni di misurazione attorno a un cerchio unitario richiede un approccio diverso al test di ipotesi. Le distribuzioni devono essere “avvolte” attorno al cerchio per essere utili e gli stimatori convenzionali come la media del campione o la varianza del campione non contengono acqua.
In questo post, condurremo il test di spaziatura di Rao per valutare l’uniformità di un set di dati circolare. Questa è una procedura di base e dovrebbe essere pensata come un’introduzione alla gestione dei dati circolari.
Guida introduttiva
Stiamo per condurre un test di ipotesi sulle tartarughe, un piccolo set di dati costituito dagli angoli di arrivo di 10 tartarughe marine verdi alla loro isola di nidificazione. Il nostro obiettivo è determinare dove gli angoli di arrivo mostrano segni di direzionalità o sono più indicativi di una dispersione casuale.
Innanzitutto, installa il pacchetto circular e collega il set di dati turtles.
install.packages("circular")require(circular)attach(turtles)
Stampa dei dati
Il pacchetto circular contiene la propria funzione di stampa, plot.circular. Osserviamo gli angoli di arrivo delle tartarughe.
plot.circular(arrival)
Ecco la trama: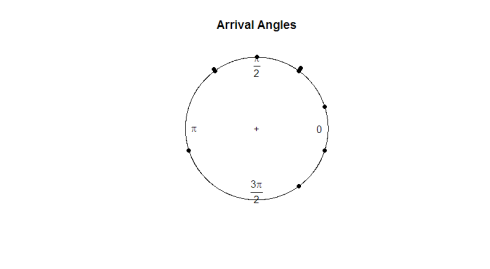
Dato il test dell’occhio, le osservazioni sembrano essere uniformi attorno al cerchio. Se vogliamo eseguire un test di ipotesi per determinare se i dati sono veramente uniformi, avremo bisogno di sviluppare una statistica di test che funzioni con i dati angolari.
Qual è un buon parametro da utilizzare? Prendendo la media del campione non ci dice molto sulla direzione dei dati (180 gradi non è una media utile di 2 gradi e 358 gradi). Nel grafico seguente, osserva come la media del campione non è utile per rappresentare la forma o la diffusione dei nostri dati.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
Ecco la trama: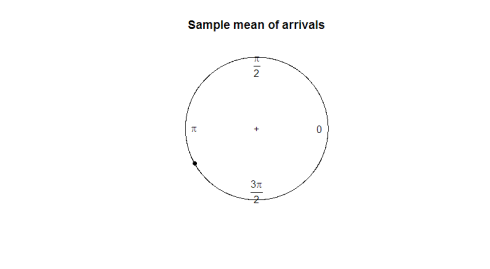
Invece, useremo un metodo che determina la direzionalità misurando lo spazio medio tra le osservazioni. Questo test è chiamato Test di spaziatura di Rao.
Test di spaziatura di Rao
Il test di spaziatura di Rao è stato sviluppato per valutare l’uniformità dei dati circolari. Utilizza lo spazio tra le osservazioni per determinare se i dati mostrano una direzionalità significativa. Se i dati sono uniformi, le osservazioni dovrebbero tendono ad essere equamente distanziate.
Ecco la statistica del test \(U\) per il test di spaziatura di Rao: $$U = 1/2\sum\limits_{i=1}^n |T_{i} – λ| $$ dove \(λ = 360/n, T_{i} = f_{i+1}-f_{i}\) e \(T_{n} = (360-f_{n})+f_{1}\)
in sostanza, il test statistici aggregati scostamenti tra punti consecutivi, ognuno ponderata per il numero totale di osservazioni nel set di dati.
Useremo la funzione rao.spacing.test() per eseguire questo test di ipotesi. La nostra ipotesi nulla dice che i dati sono di una distribuzione uniforme, mentre gli stati alternativi i dati mostrano segni di direzionalità. Facciamo il test.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
Con una statistica di test di 127 che scende al di sotto del valore critico di 161, i dati non riescono a inclinarsi in modo significativo in qualsiasi direzione. Non possiamo respingere l’ipotesi che gli arrivi delle tartarughe siano di una distribuzione uniforme.
Conclusione
Il test di spaziatura di Rao ha determinato che i dati non mostrano segni di tendenze direzionali. Non possiamo respingere l’ipotesi nulla di uniformità e assumeremo uniformità per quanto riguarda la direzione di arrivo. Mentre questo post è stato un tutorial relativamente di base, molte persone nella comunità di scienza dei dati non hanno lavorato con i dati circolari prima. Si tratta di un subtopic interessante per tuffarsi a così come un giovane campo di statistiche che è ancora in evoluzione.
Osservazioni finali
Vorrei estendere credito a S. Rao Jammalamadaka PhD, dell’Università della California, Santa Barbara, e il suo libro di testo “Argomenti in Statistica circolare” per suscitare il mio interesse nel campo della statistica circolare.