Conoscenza presunta
Gli studenti avranno avuto una vasta esperienza informale con la geometria negli anni precedenti, e questo fornirà una buona base intuitiva per l’approccio più sistematico alla geometria appropriato negli anni 7-10. Gli argomenti particolari degli anni F-6 rilevanti per questo modulo sono:
- L’uso di bussole e righelli e l’attento disegno di figure geometriche.
- Tipi di angoli, compresi almeno angoli retti, angoli acuti, angoli ottusi e
angoli riflessi. - Triangoli, tra cui un’introduzione informale a isoscele e triangoli equilateri.
- Quadrilateri, tra cui un’introduzione informale a quadrati, rettangoli, parallelogrammi, trapezi e rombi.
- Esperienza informale con traduzioni, riflessioni, rotazioni e ingrandimenti,
e con simmetria nel contesto di attività come piegare un triangolo isoscele, un rettangolo o un rombo.
Motivazione
 La geometria viene utilizzata per modellare il mondo che ci circonda. Una vista dei tetti delle case rivela triangoli, trapezi e rettangoli, mentre i modelli di piastrelle nei pavimenti e nei bagni utilizzano esagoni, pentagoni, triangoli e quadrati.
La geometria viene utilizzata per modellare il mondo che ci circonda. Una vista dei tetti delle case rivela triangoli, trapezi e rettangoli, mentre i modelli di piastrelle nei pavimenti e nei bagni utilizzano esagoni, pentagoni, triangoli e quadrati.
Costruttori, piastrellisti, architetti, grafici e web designer utilizzano abitualmente idee geometriche nel loro lavoro. La classificazione di tali oggetti geometrici e lo studio delle loro proprietà sono molto importanti. La geometria ha anche molte applicazioni nell’arte.
Proprio come l’aritmetica ha i numeri come i suoi oggetti di base di studio, così punti, linee e cerchi sono gli elementi costitutivi di base della geometria piana.
Nella geometria della scuola secondaria, iniziamo con una serie di idee intuitive (punti, linee e angoli) che non sono affatto facili da definire con precisione, seguite da alcune definizioni (angoli verticalmente opposti, linee parallele e così via) e da queste deduciamo fatti importanti, che sono spesso indicati come teoremi. Nella scuola secondaria, il livello di rigore dovrebbe svilupparsi lentamente da un anno all’altro, ma in ogni fase una chiara impostazione è molto importante e dovrebbe essere sottolineata.
Così geometria dà agli studenti l’opportunità di sviluppare la loro intuizione geometrica, che ha applicazioni in molti settori della vita, e anche per imparare a costruire ragionamenti logici e fare deduzioni, in un ambiente che è, per la maggior parte, indipendente
di numero.
Content
Punti e linee
Gli oggetti più semplici nella geometria piana sono punti e linee. Perché sono così semplici, è difficile dare definizioni precise di loro, così invece ci proponiamo di dare agli studenti una descrizione approssimativa delle loro proprietà che sono in linea con la nostra intuizione. Un punto segna una posizione ma non ha dimensioni. In pratica, quando disegniamo un punto ha chiaramente una larghezza definita, ma rappresenta un punto nella nostra immaginazione. Una linea non ha larghezza e si estende infinitamente in entrambe le direzioni. Quando disegniamo una linea ha larghezza e ha estremità, quindi non è davvero una linea, ma rappresenta una linea nella nostra immaginazione. Dati due punti distinti A e B, allora c’è una (e solo una) linea che passa attraverso entrambi i punti. Usiamo lettere maiuscole per fare riferimento a punti e linee di nome indicando due punti sulla linea, o usando lettere minuscole come  e m. Quindi, la linea indicata di seguito è indicata come la linea AB o come la linea
e m. Quindi, la linea indicata di seguito è indicata come la linea AB o come la linea  .
.

Date due linee distinte, ci sono due possibilità: possono incontrarsi in un singolo punto o non possono mai incontrarsi, indipendentemente da quanto siano estesi (o prodotti). Le linee che non si incontrano mai sono chiamate parallele. Nel secondo diagramma, scriviamo AB / / CD.
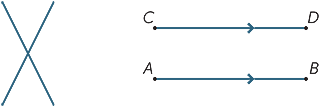
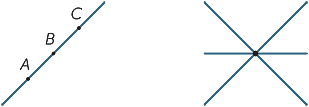
Tre (o più) punti che si trovano su una linea retta sono chiamati collineari.
Tre (o più) linee che si incontrano in un singolo punto sono chiamate simultanee.
|
|
|
| Collineare |
Simultaneo |
Esercizio 1
Disegna tre linee che non sono simultanee in modo tale che non ci siano due linee parallele.
Esercizio 2
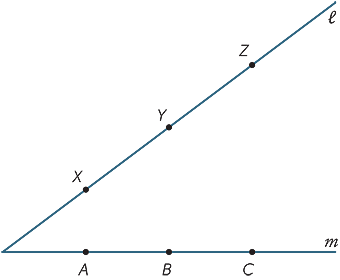
Fare una grande copia del diagramma sottostante. I punti X, Y, Z sono punti sulla linea  e A, B, C sono punti sulla linea m. Join AY e XB chiamano la loro intersezione R. Join BZ e YC e chiamano la loro intersezione P. Join CX e ZA e chiamano la loro intersezione Q. Cosa noti dei punti P, Q, R? (Questo risultato è chiamato teorema di Pappus, c.340 DC.)
e A, B, C sono punti sulla linea m. Join AY e XB chiamano la loro intersezione R. Join BZ e YC e chiamano la loro intersezione P. Join CX e ZA e chiamano la loro intersezione Q. Cosa noti dei punti P, Q, R? (Questo risultato è chiamato teorema di Pappus, c.340 DC.)
Intervalli, raggi e angoli
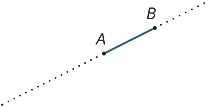 Supponiamo che A e B siano due punti su una linea. L’intervallo
Supponiamo che A e B siano due punti su una linea. L’intervallo
AB è la parte della linea tra A e B, inclusi i due endpoint.
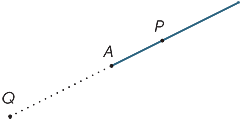 Il punto A nel diagramma divide la linea in due pezzi chiamati raggi. Il raggio AP è quel raggio che contiene il punto P (e il punto A).
Il punto A nel diagramma divide la linea in due pezzi chiamati raggi. Il raggio AP è quel raggio che contiene il punto P (e il punto A).
Angoli
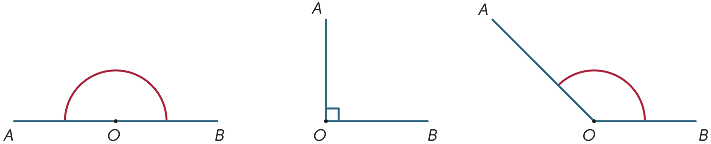
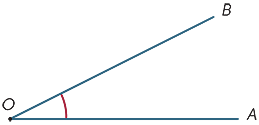
 Nel diagramma, la regione ombreggiata tra i raggi OA e OB è chiamata angolo AOB o angolo BOA. Il segno dell’angolo
Nel diagramma, la regione ombreggiata tra i raggi OA e OB è chiamata angolo AOB o angolo BOA. Il segno dell’angolo ![]() è scritto in modo da scrivere
è scritto in modo da scrivere ![]() AOB.
AOB.
 La regione ombreggiata all’esterno è chiamata angolo riflesso formato da OA e OB. Il più delle volte, a meno che non specifichiamo la parola riflesso, tutti i nostri angoli si riferiscono all’area tra i raggi e non al di fuori di essi.
La regione ombreggiata all’esterno è chiamata angolo riflesso formato da OA e OB. Il più delle volte, a meno che non specifichiamo la parola riflesso, tutti i nostri angoli si riferiscono all’area tra i raggi e non al di fuori di essi.
La dimensione di un angolo
 Immagina che il raggio OB sia ruotato attorno al punto O finché non giace lungo OA. La quantità di rotazione è chiamata la dimensione dell’angolo AOB. Allo stesso modo possiamo definire la dimensione dell’angolo riflesso.
Immagina che il raggio OB sia ruotato attorno al punto O finché non giace lungo OA. La quantità di rotazione è chiamata la dimensione dell’angolo AOB. Allo stesso modo possiamo definire la dimensione dell’angolo riflesso.
Useremo spesso piccole lettere greche, α, β, γ, … per rappresentare la dimensione di un angolo.
La dimensione dell’angolo corrispondente a una rivoluzione completa fu divisa (dai babilonesi) in 360 parti uguali, che chiamiamo gradi. (Probabilmente hanno scelto 360 poiché era vicino al numero di giorni in un anno.) Quindi, la dimensione di un angolo retto è 180° e la dimensione di un angolo retto è 90°. Altri angoli possono essere misurati (approssimativamente) usando un goniometro.
|
|
||
| angolo retto | angolo retto |
angolo Ottuso |
gli Angoli sono classificati secondo la loro dimensione. Diciamo che un angolo con dimensione α è acuto
(una parola che significa ‘sharp’) se 0° < α <90°, α è ottuso (una parola che significa ‘blunt’) se
90° < α < 180° e α è riflesso se 180° < α < 360°.
Poiché il goniometro ha due scale, gli studenti devono fare attenzione quando disegnano e
misurano gli angoli. È un esercizio utile usare un goniometro per disegnare alcuni angoli come 30°, 78°, 130°, 163°.
Esercizio 3
 Piegare un foglio di carta A4 corrispondente agli angoli opposti (diagonalmente). Disegna una linea lungo la piega che si forma e misura gli angoli tra la piega e il lato.
Piegare un foglio di carta A4 corrispondente agli angoli opposti (diagonalmente). Disegna una linea lungo la piega che si forma e misura gli angoli tra la piega e il lato.
Nell’esercizio sopra, i due angoli insieme formano una linea retta e quindi si aggiungono a 180°. Due angoli che si aggiungono a 180 ° sono chiamati angoli supplementari; quindi 45° e 135° sono angoli supplementari.
Due angoli che si aggiungono a 90° sono chiamati complementari; quindi 23° e 67° sono
angoli complementari.
Angoli in un punto
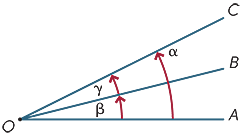 Si dice che due angoli in un punto siano adiacenti se condividono un raggio comune. Quindi, nel diagramma,
Si dice che due angoli in un punto siano adiacenti se condividono un raggio comune. Quindi, nel diagramma, ![]() AOB e
AOB e ![]() BOC sono adiacenti.
BOC sono adiacenti.
È possibile aggiungere angoli adiacenti, quindi nel diagramma
α = β + γ.
Quando due linee si intersecano, si formano quattro angoli nel punto di intersezione.
Nel diagramma, gli angoli contrassegnati ![]() AOX e
AOX e ![]() BOY sono chiamati verticalmente opposti.
BOY sono chiamati verticalmente opposti.
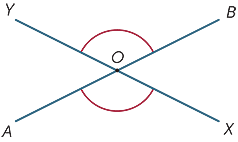 Dal
Dal
-
 AOX è il supplemento di
AOX è il supplemento di  BOX (angolo retto).
BOX (angolo retto). -
 BOY è anche il supplemento di
BOY è anche il supplemento di  BOX (angolo retto),
BOX (angolo retto),
possiamo concludere che questi angoli verticalmente opposti,![]() AOX e
AOX e ![]() BOY sono uguali. Abbiamo quindi la nostra prima
BOY sono uguali. Abbiamo quindi la nostra prima
importante affermazione geometrica:
Gli angoli verticalmente opposti sono uguali.
Un risultato in geometria (e in matematica in generale) è spesso chiamato teorema. Un teorema è un’affermazione importante che può essere dimostrata dalla deduzione logica. L’argomento di cui sopra è una prova del teorema; a volte le prove sono presentate formalmente dopo l’affermazione del teorema.
 Se due linee si intersecano in modo che tutti e quattro gli angoli siano angoli retti, si dice che le linee siano perpendicolari.
Se due linee si intersecano in modo che tutti e quattro gli angoli siano angoli retti, si dice che le linee siano perpendicolari.
Angoli in un punto − Argomenti geometrici
I seguenti motivi possono essere utilizzati in argomenti geometrici:
- Gli angoli adiacenti possono essere aggiunti o sottratti.
- Gli angoli in una rivoluzione si aggiungono a 360°.
- Gli angoli in linea retta si aggiungono a 180°.
- Gli angoli verticalmente opposti sono uguali.
Linee trasversali e parallele
 Una linea trasversale è una linea che incontra altre due linee.
Una linea trasversale è una linea che incontra altre due linee.
Angoli corrispondenti
Vari angoli sono formati dal trasversale. Nei diagrammi seguenti, i due angoli contrassegnati sono chiamati angoli corrispondenti.
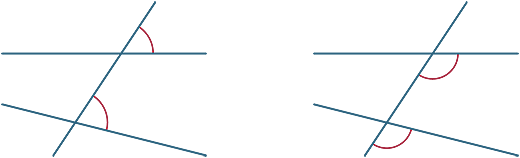
 Vediamo ora cosa succede quando le due linee tagliate dal trasversale sono parallele.
Vediamo ora cosa succede quando le due linee tagliate dal trasversale sono parallele.
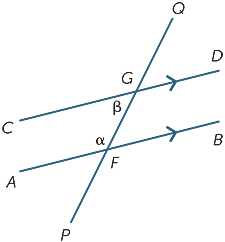
Inituitivamente, se l’angolo α fosse maggiore di β, CD attraverserebbe AB a sinistra di F e se fosse inferiore a β, attraverserebbe a destra di F. Quindi, poiché le linee non si incrociano affatto, α non può essere né inferiore né superiore a β e quindi uguale a β.
In alternativa, immagina di tradurre l’angolo QGD lungo GF fino a quando G coincide con F. Poiché le linee sono parallele, ci aspetteremmo che l’angolo α coincida con l’angolo β. Questa osservazione ci porta a congetturare che:
Gli angoli corrispondenti formati da linee parallele sono uguali.
Non possiamo dimostrare questo risultato, anche se abbiamo dimostrato che è geometricamente plausibile. Lo accetteremo come un assioma della geometria. Un assioma è un’affermazione che non possiamo dimostrare, ma che è intuitivamente ragionevole. Si noti che molti dei fatti che abbiamo già dichiarato come: angoli adiacenti possono essere aggiunti, e due punti determinano una linea ecc., sono anche assiomi, anche se non li abbiamo esplicitamente dichiarati in questo modo.
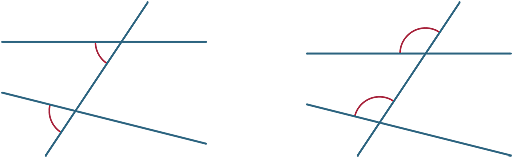
Angoli alternativi
In ogni diagramma i due angoli contrassegnati sono chiamati angoli alternativi (poiché si trovano su lati alternativi del trasversale).

 Se le linee AB e CD sono parallele, gli angoli alternativi sono uguali. Questo risultato può ora essere dimostrato.
Se le linee AB e CD sono parallele, gli angoli alternativi sono uguali. Questo risultato può ora essere dimostrato.
![]() DGQ = α (angoli corrispondenti, AB / / CD)
DGQ = α (angoli corrispondenti, AB / / CD)
![]() DGQ = β (angoli verticalmente opposti a G)
DGQ = β (angoli verticalmente opposti a G)
Quindi α = β.
Per riassumere:
Gli angoli alternativi formati da linee parallele sono uguali.
Angoli co-interni
Infine, in ogni diagramma sottostante, i due angoli marcati sono chiamati angoli co-interni e si trovano sullo stesso lato del trasversale.

Se le linee AB e CD sono parallele, allora è ovvio che gli angoli co-interni non sono uguali ma risulta che sono supplementari, cioè la loro somma è di 180° .
 Questo è un risultato che è anche facile da dimostrare:
Questo è un risultato che è anche facile da dimostrare:
![]() BFG = β (angoli alternati, AB ||CD)
BFG = β (angoli alternati, AB ||CD)
α + β = 180° (angolo retto a F)
Per riassumere:
Gli angoli co-interni formati da linee parallele sono supplementari.
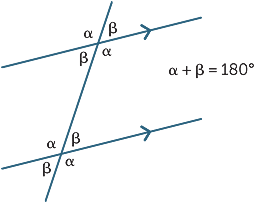 I tre risultati possono essere riassunti
I tre risultati possono essere riassunti
dal seguente diagramma:
Esempi numerici
Date informazioni sugli angoli in un diagramma, possiamo utilizzare i risultati di cui sopra per trovare la dimensione di altri angoli nel diagramma. Questa è un’abilità semplice ma molto importante, spesso definita informalmente come angle chasing. Nel risolvere i problemi, la sequenza di passaggi non è sempre unica. Ci possono essere diversi approcci diversi, ma ugualmente validi.
Ad esempio, nel diagramma seguente, cerchiamo la dimensione dell’angolo BAC.

![]() DCA = 102° (angoli alternati, AC / BD)
DCA = 102° (angoli alternati, AC / BD)
![]() BAC = 78° (angoli interni co, AB / / CD)
BAC = 78° (angoli interni co, AB / / CD)
Esercizio 4
Utilizzare una sequenza alternatie di passi per trovare ![]() BAC.
BAC.
Esercizio 5
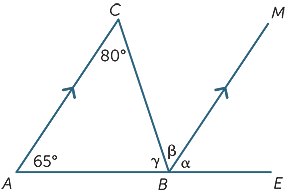 Usando solo le proprietà delle linee parallele, trova (con le ragioni) gli angoli mancanti nel diagramma seguente.
Usando solo le proprietà delle linee parallele, trova (con le ragioni) gli angoli mancanti nel diagramma seguente.
Esercizio 6
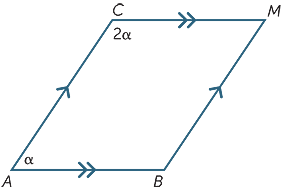
Trova il valore di α nel diagramma seguente.
Dichiarazioni converse
Molte affermazioni in matematica hanno un converse, in cui l’implicazione va nella direzione opposta. Ad esempio, l’istruzione
‘Ogni numero pari termina in 0, 2, 4, 6 o 8.’
ha converse
‘Ogni numero che termina in 0, 2, 4, 6 o 8 è pari.’
Questa particolare affermazione e il suo contrario sono entrambi veri, ma questo non è sempre
il caso.
Ad esempio, le seguenti due istruzioni sono converse l’una dell’altra:
‘Ogni multiplo di 4 è un numero pari.’
‘ Ogni numero pari è un multiplo di 4.’
e qui, la prima affermazione è vera, ma la seconda è falsa.
Esercizio 7
Annotare:
a![]() una vera dichiarazione geometrica il cui contrario è anche vero,
una vera dichiarazione geometrica il cui contrario è anche vero,
b![]() falsa dichiarazione geometrica il cui contrario è vero,
falsa dichiarazione geometrica il cui contrario è vero,
c ![]() una falsa dichiarazione geometrica il cui contrario è anche falso.
una falsa dichiarazione geometrica il cui contrario è anche falso.
I Teoremi Converse per le rette parallele
Abbiamo visto che gli angoli corrispondenti formati da rette parallele sono uguali. Possiamo scrivere la dichiarazione inversa come segue.
Istruzione: se le linee sono parallele, gli angoli corrispondenti sono uguali.
Converse: Se gli angoli corrispondenti sono uguali, le linee sono parallele.
Anche l’istruzione inversa è vera e viene spesso utilizzata per dimostrare che due linee sono parallele. Lo stesso vale per gli angoli alternati e co-interni.
Istruzione: se le linee sono parallele, gli angoli alternativi sono uguali.
Converse: se gli angoli alternativi sono uguali, le linee sono parallele.
Istruzione: se le linee sono parallele, gli angoli co-interni sono supplementari.
Converse: Se gli angoli co-interni sono supplementari, le linee sono parallele.
Quindi, in ogni diagramma, le linee AB e CD sono parallele.

Esercizio 8
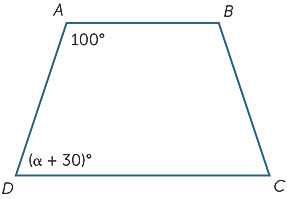 Quale valore di α renderà AB parallelo al CD?
Quale valore di α renderà AB parallelo al CD?
Prove delle tre conversazioni
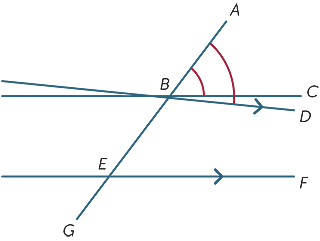 Supponiamo che gli angoli corrispondenti formati dal trasversale siano uguali e mostriamo che le linee sono parallele.
Supponiamo che gli angoli corrispondenti formati dal trasversale siano uguali e mostriamo che le linee sono parallele.
Nel diagramma, supponiamo che ![]() ABC =
ABC = ![]() BEF.
BEF.
Se BC ed EF non sono paralleli, quindi disegnare
BD parallelo a EF.
Ora poiché BD ed EF sono paralleli ![]() ABD =
ABD = ![]() BEF e così
BEF e così ![]() ABC =
ABC = ![]() ABD che è chiaramente impossibile a meno che le linee BC e BD non siano le stesse. Quindi le linee BC ed EF sono parallele.
ABD che è chiaramente impossibile a meno che le linee BC e BD non siano le stesse. Quindi le linee BC ed EF sono parallele.
Le altre prove seguono nello stesso modo.
Esercizio 9
Dare una prova del secondo teorema di converse (angoli alternativi).
Somma angolare di un triangolo
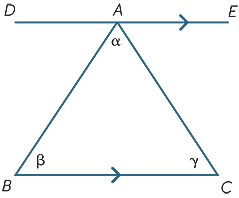 I risultati della sezione precedente possono essere utilizzati per dedurre uno dei fatti più importanti della geometria: la somma dell’angolo di un triangolo è di 180° .
I risultati della sezione precedente possono essere utilizzati per dedurre uno dei fatti più importanti della geometria: la somma dell’angolo di un triangolo è di 180° .
Iniziamo con il triangolo ABC con angoli α, β, γ come mostrato. Disegna la linea DAE parallela a BC. Allora,
![]() DAB = β (angoli alternati, BC / / DE)
DAB = β (angoli alternati, BC / / DE)
![]() EAC = γ (angoli alternati, BC||DE)
EAC = γ (angoli alternati, BC||DE)
α+ β + γ = 180° (angolo retto).
Quindi, abbiamo dimostrato il teorema
La somma degli angoli in un triangolo è di 180°.
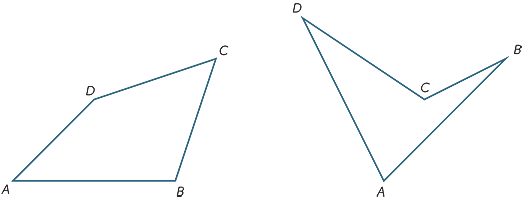
Un quadrilatero è una figura piana delimitata da quattro lati.
Esercizio 10
Dividendo il quadrilatero ABCD in due triangoli, trova la somma degli angoli.
Link in avanti
Il materiale in questo modulo ha iniziato a collocare la geometria su una base ragionevolmente sistematica di oggetti accuratamente definiti, assiomi che devono essere assunti e teoremi che abbiamo dimostrato. Su questa base, possiamo sviluppare un resoconto sistematico della geometria piana che coinvolge:
- Teorema di Pitagora
- triangoli di congruenza e congruenti
- triangoli di similarità e simili
- triangoli isosceli e equilateri
- quadrilateri speciali, compresi quadrati, rettangoli, parallelogrammi, rombi e trapezi
- la geometria dei cerchi.
La geometria piana sarà fondamentale anche in molte altre aree della matematica degli anni 7-10:
- trasformazioni
- geometria tridimensionale
- aree e volumi
- trigonometria
- geometria delle coordinate
- i grafici di cerchi e parabole.
Le idee di tangenti e aree portano a loro volta al calcolo negli anni 11-12.
Storia e applicazione
Storia
Le incredibili costruzioni delle piramidi e degli enormi templi dell’Egitto rivelano che gli egiziani dovevano avere un’ottima conoscenza e comprensione della geometria di base, almeno a livello pratico. D’altra parte, non ci sono prove che abbiano sistematizzato tale conoscenza in alcun modo formale. Questo è stato lasciato agli antichi greci. Non abbiamo una conoscenza dettagliata di tale sistematizzazione, ad eccezione dell’affermazione che Thales (ca. 624 a. C. – ca. 546 AC) ha dato le prime ‘prove’ di fatti geometrici che ha segnato gli inizi della geometria deduttiva. La scuola pitagorica ha continuato questo lavoro e Platone (428 AC -348 AC) è chiaramente attingendo al lavoro dei matematici precedenti quando menziona fatti geometrici nei suoi scritti. Il dialogo geometrico nella sua opera il Meno, in cui Socrate ottiene un ragazzo schiavo per arrivare a un teorema geometrico da una serie di deduzioni logiche, merita una lettura. Se le origini della geometria non sono chiare, il “prodotto finale” non lo è. Euclide (323-283 AC), scrivendo ad Alessandria, produsse un lavoro notevole, chiamato the Elements, che rimase il libro di testo standard in geometria per più di 2000 anni. In questo lavoro, Euclide stabilisce una serie di definizioni (come per punti e linee), postulati e nozioni comuni. (In questi giorni li chiamiamo assiomi.) Da questi, ha logicamente sviluppato, in un ordine molto accuratamente scelto, un gran numero di teoremi che generalmente si riferiscono a come Geometria Euclidea. Ci sono una serie di altri risultati geometrici, come il teorema di Pappus, che sono stati scoperti dopo Euclide, ma questi non sono generalmente coperti nella scuola secondaria.
Uno dei cinque postulati di Euclide non era ovviamente vero come gli altri sembravano essere. Una versione di esso, nota come Assioma di Playfair afferma che: Data una linea e un punto P, non su
e un punto P, non su , c’è una e una sola linea parallela a
, c’è una e una sola linea parallela a  che passa attraverso P. Nel 19 ° secolo, un certo numero di matematici ha posto la domanda ‘Cosa succede se neghiamo questo postulato?”Questo viene fatto assumendo che o non esiste una tale linea parallela, o dicendo che esiste più di una tale linea. Ciò ha portato allo sviluppo di geometrie non euclidee, una delle quali si è rivelata uno dei buoni modelli per l’universo.
che passa attraverso P. Nel 19 ° secolo, un certo numero di matematici ha posto la domanda ‘Cosa succede se neghiamo questo postulato?”Questo viene fatto assumendo che o non esiste una tale linea parallela, o dicendo che esiste più di una tale linea. Ciò ha portato allo sviluppo di geometrie non euclidee, una delle quali si è rivelata uno dei buoni modelli per l’universo.
Applicazioni
In un senso molto reale, la geometria e l’intuizione geometrica costituiscono le basi di tutti
Matematica − la geometria porta alla geometria coordinata che porta al calcolo e
tutte le sue numerose applicazioni − e quindi è cruciale nel curriculum.
A livello più pratico, costruttori, geometri, ingegneri e architetti sono stati pesanti utilizzatori di geometria e idee geometriche per secoli. Più recentemente, con lo sviluppo dei computer, artisti grafici e web designer si sono uniti a questo gruppo di persone che hanno bisogno e usano la geometria nel loro lavoro. Quando è stato chiesto di recente quanto sia utile la geometria, Jim Kelly, uno scienziato applicato, ha detto:… la geometria è una parte importante del design, del disegno e della modellazione al computer. Inoltre è usato frequentemente in … corsi di fisica e altre scienze fisiche come parte della comprensione degli effetti dei carichi sulle strutture e sui punti di bilanciamento (centri di gravità) per i solidi compositi. In chimica, la comprensione della geometria di una molecola è correlata alla comprensione delle proprietà delle sostanze. Esistono molti altri esempi. (dal sito web Chiedi uno scienziato.)
Una storia della matematica: Un’introduzione, 3a edizione, Victor J. Katz, Addison-Wesley, (2008)
Storia della Matematica, D. E. Smith, Dover publications New York, (1958)
RISPOSTE AGLI ESERCIZI
ESERCIZIO 1
ESERCIZIO 2
I punti collineari
ESERCIZIO 3
60°
ESERCIZIO 4
![]() DBA = 102° (angoli corrispondenti, AB||CD)
DBA = 102° (angoli corrispondenti, AB||CD)
![]() BAC = 78° (co-angoli interni, AC||BD)
BAC = 78° (co-angoli interni, AC||BD)
ESERCIZIO 5
α = 65°![]() (angoli corrispondenti, AC||BM)
(angoli corrispondenti, AC||BM)
β = 80°![]() (angoli alterni, AC||BM)
(angoli alterni, AC||BM)
γ + β = 115°![]() (co-angoli interni, AC||BM)
(co-angoli interni, AC||BM)
Quindi, γ = 35°
(Questa è la struttura per una prova del risultato che la somma degli angoli di un triangolo è 180°)
ESERCIZIO 6
α = 60°
ESERCIZIO 7
a ![]() Un quadrilatero con ciascuno dei suoi angoli interni un angolo retto è un rettangolo.
Un quadrilatero con ciascuno dei suoi angoli interni un angolo retto è un rettangolo.
Converse: Ogni angolo interno di un rettangolo è un angolo retto.
b![]() Un rettangolo è un quadrato
Un rettangolo è un quadrato
Converse: un quadrato è Un rettangolo
c![]() L’angolo somma degli angoli interni di un triangolo è di 200°
L’angolo somma degli angoli interni di un triangolo è di 200°
Converse: Un poligono per il quale la somma degli angoli interni è di 200° è un triangolo.
ESERCIZIO 8
α = 50°
ESERCIZIO 9
Ci riferiamo allo stesso diagramma.
Posiziona un punto H sulla linea EF a sinistra di E.
![]() CBE =
CBE = ![]() BEH
BEH
Se BC ed EF non sono paralleli, disegna BD parallelo a EF.
Poiché BD ed EF sono paralleli, ![]() EBD=
EBD= ![]() BEH, che è chiaramente impossibile a meno che le linee BC e BD non siano le stesse.
BEH, che è chiaramente impossibile a meno che le linee BC e BD non siano le stesse.
Quindi le linee BC ed EF sono parallele.
ESERCIZIO 10
360°
Il progetto Improving Mathematics Education in Schools (TIMES) 2009-2011 è stato finanziato dal Dipartimento dell’Istruzione, dell’occupazione e delle relazioni sul posto di lavoro del governo australiano.
Le opinioni espresse qui sono quelle dell’autore e non rappresentano necessariamente le opinioni del Dipartimento del governo australiano per l’Istruzione, l’occupazione e le relazioni sul posto di lavoro.
© Università di Melbourne per conto dell’International Centre of Excellence for Education in Mathematics (ICE-EM), la divisione educativa dell’Australian Mathematical Sciences Institute (AMSI), 2010 (salvo dove diversamente indicato). Questo lavoro è distribuito sotto la licenza Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()