Questa è una guida passo passo su come eseguire l’analisi del cluster k-means su un foglio di calcolo Excel dall’inizio alla fine. Si prega di notare che esiste un modello di Excel che esegue automaticamente l’analisi del cluster disponibile per il download gratuito su questo sito web. Ma se vuoi sapere come eseguire un clustering k-means su Excel, allora questo articolo è per te.
Oltre a questo articolo, ho anche un video walk-through di come eseguire l’analisi del cluster in Excel.
- Fase Uno – Iniziare con il set di dati
- Passo a Due, Se solo due variabili, utilizzare un grafico a dispersione su Excel
- Fase tre – Calcolare la distanza da ogni punto dati al centro di un cluster
- Come funziona il calcolo?
- Fase quattro – Calcolare la media (media) di ciascun set di cluster
- Passo cinque-Ripetere il passo 3-la distanza dalla media riveduta
- Fase finale-Grafico e riassumere i cluster
Fase Uno – Iniziare con il set di dati
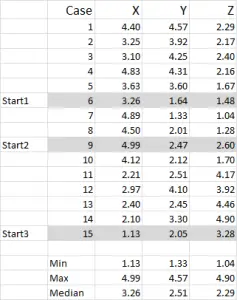
Figura 1
Per questo esempio sto usando 15 casi (o rispondenti), dove abbiamo i dati per tre variabili – genericamente etichettati X, Y e Z.
Dovresti notare che i dati sono ridimensionati 1-5 in questo esempio. I tuoi dati possono essere in qualsiasi forma tranne che per una scala di dati nominale (vedi l’articolo di quali dati utilizzare).
NOTA: preferisco utilizzare i dati in scala, ma non è obbligatorio. La ragione di ciò è “contenere” eventuali valori anomali. Diciamo, ad esempio, che sto usando i dati sul reddito (una misura demografica) – la maggior parte dei dati potrebbe essere di circa 4 40.000 a $100.000, ma ho una persona con un reddito di $5m. È solo più facile per me classificare quella persona nella fascia di reddito “oltre $250.000” e scalare il reddito 1-9 – ma dipende da te a seconda dei dati con cui stai lavorando.
Puoi vedere da questo esempio che sono state evidenziate tre posizioni di partenza-discuteremo quelle nel passaggio tre di seguito.
Passo a Due, Se solo due variabili, utilizzare un grafico a dispersione su Excel
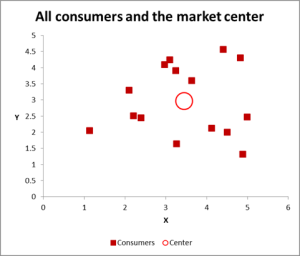
Figura 2
In questo cluster analysis esempio stiamo utilizzando tre variabili – ma se hai solo due variabili cluster, quindi un grafico a dispersione è un ottimo modo per iniziare. E, a volte, è possibile raggruppare i dati tramite mezzi visivi.
Come puoi vedere in questo grafico a dispersione, ogni singolo caso (quello che chiamo un consumatore per questo esempio) è stato mappato, insieme alla media (media) per tutti i casi (il cerchio rosso).
A seconda di come si visualizzano i dati/grafico, sembra esserci un numero di cluster. In questo caso, è possibile identificare tre o quattro cluster relativamente distinti, come mostrato in questo grafico successivo.
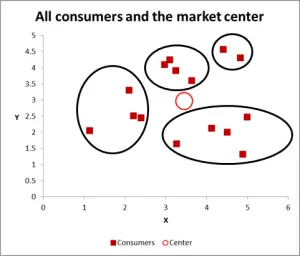
Figura 3
Con questo grafico successivo, ho visibilmente identificato il probabile cluster e li ho cerchiati. Come ho suggerito, un buon approccio quando ci sono solo due variabili da considerare – ma in questo caso abbiamo tre variabili (e potresti averne di più), quindi questo approccio visivo funzionerà solo per i set di dati di base – quindi ora diamo un’occhiata a come fare il calcolo di Excel per k-means clustering.
Fase tre – Calcolare la distanza da ogni punto dati al centro di un cluster
Per questo esempio walk-through, supponiamo di voler identificare solo tre segmenti/cluster. Sì, ci sono quattro cluster evidenti nel diagramma sopra, ma che guarda solo due delle variabili. Si prega di notare che è possibile utilizzare questo approccio Excel per identificare il numero di cluster come ti piace-basta seguire lo stesso concetto come spiegato di seguito.
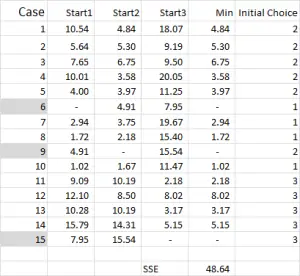
Figura 4
Per k-means clustering in genere si selezionano alcuni casi casuali (punti di partenza o semi) per avviare l’analisi.
In questo esempio – dato che voglio creare tre cluster, avrò bisogno di tre punti di partenza. Per questi punti di partenza ho selezionato i casi 6, 9 e 15 – ma anche eventuali punti casuali potrebbero essere adatti.
Il motivo per cui ho selezionato questi casi è perché – guardando solo la variabile X – il caso 6 era la mediana, il caso 9 era il massimo e il caso 15 era il minimo. Ciò suggerisce che questi tre casi sono in qualche modo diversi l’uno dall’altro, quindi buoni punti di partenza man mano che sono sparsi.
Si prega di fare riferimento all’articolo sul perché l’analisi cluster a volte genera risultati diversi.
Riferendosi all’output della tabella – questo è il nostro primo calcolo in Excel e genera la nostra “scelta iniziale” di cluster. Start 1 è i dati per il caso 6, start 2 è il caso 9 e start 3 è il caso 15. Si noti che l’intersezione di ciascuno di questi dà un 0 ( – ) nella tabella.
Come funziona il calcolo?
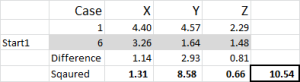
Figura 5
Diamo un’occhiata al primo numero nella tabella – caso 1, inizio 1 = 10.54.
Ricorda che abbiamo arbitrariamente designato il Caso 6 come il nostro punto di partenza casuale per il Cluster 1. Vogliamo calcolare la distanza e usiamo la somma dei quadrati metodo-come mostrato qui. Calcoliamo la differenza tra ciascuno dei tre punti dati nel set, quindi quadriamo le differenze e quindi le sommiamo.
Possiamo farlo “meccanicamente” come mostrato qui – ma Excel ha una formula incorporata da usare: SUMXMY2-questo è molto più efficiente da usare.
Facendo riferimento alla Figura 4, troviamo quindi la distanza minima per ogni caso da ciascuno dei tre punti di partenza – questo ci dice quale cluster (1, 2 o 3) a cui il caso è più vicino – che è mostrato nella ‘colonna scelta iniziale’.
Fase quattro – Calcolare la media (media) di ciascun set di cluster
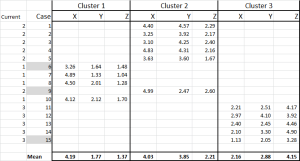
Figura 6
Ora abbiamo assegnato ogni caso al suo cluster iniziale-e possiamo disporlo usando un’istruzione IF in una tabella (come mostrato in Figura 6).
Nella parte inferiore della tabella, abbiamo la media (media) di ciascuno di questi casi. N0w-invece di fare affidamento su un solo punto dati “rappresentativo” – abbiamo un insieme di casi che rappresentano ciascuno.
Passo cinque-Ripetere il passo 3-la distanza dalla media riveduta
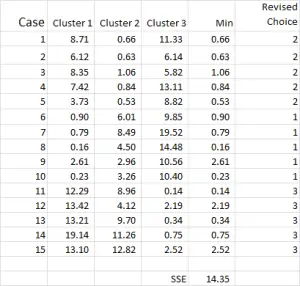
Figura 7
Il processo di analisi del cluster diventa ora una questione di ripetere i passaggi 4 e 5 (iterazioni) fino a quando i cluster si stabilizzano.
Ogni volta che usiamo la media rivista per ogni cluster. Pertanto, la figura 7 mostra la nostra seconda iterazione – ma questa volta stiamo usando i mezzi generati nella parte inferiore della Figura 6 (invece dei punti di partenza dalla Figura 1).
Ora puoi vedere che c’è stato un leggero cambiamento nell’applicazione cluster, con il caso 9 – uno dei nostri punti di partenza – riallocato.
Puoi anche vedere la somma dell’errore quadrato (SSE) calcolato in basso – che è la somma di ciascuna delle distanze minime. Il nostro obiettivo è ora ripetere i passaggi 4 e 5 fino a quando l’SSE mostra solo miglioramenti minimi e/o le modifiche all’allocazione del cluster sono minori su ogni iterazione.
Fase finale-Grafico e riassumere i cluster
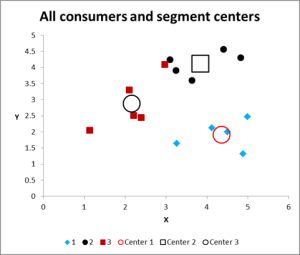
Figura 8
Dopo aver eseguito più iterazioni, ora abbiamo l’output per rappresentare graficamente e riassumere i dati.
Ecco il grafico di output per questo esempio di Excel di analisi cluster.
Come puoi vedere, ci sono tre cluster distinti mostrati, insieme ai centroidi (media) di ciascun cluster – i simboli più grandi.
Possiamo anche presentare questi dati in un modulo di tabella, se necessario, come abbiamo elaborato in Excel.
Si prega di dare un’occhiata al caso nel Cluster 3 – il piccolo quadrato rosso proprio accanto al punto nero nella parte superiore del grafico. Quel caso si trova lì a causa dell’influenza della terza variabile, che non è mostrata su questo grafico a due variabili.