Valutazione | Biopsychology | Comparativa |Cognitivo | di Sviluppo | e Lingua | e differenze Individuali |Personalità | Filosofia | Social |
Metodi | Statistiche |Clinica | Educativi | Industriali |Professionali |Mondo psicologia |
Statistiche:Il metodo scientifico · metodi di Ricerca · disegno Sperimentale · statistiche di Laurea corsi · test Statistici · la teoria dei giochi · teoria delle Decisioni
Si prega di contribuire a migliorare questa pagina da soli, se è possibile..
L’analisi del cluster o clustering è una tecnica comune per l’analisi statistica dei dati, che viene utilizzata in molti campi, tra cui l’apprendimento automatico, il data mining, il riconoscimento di pattern, l’analisi delle immagini e la bioinformatica. Il clustering è la classificazione di oggetti simili in gruppi diversi, o più precisamente, il partizionamento di un set di dati in sottoinsiemi (cluster), in modo che i dati in ciascun sottoinsieme (idealmente) condividano alcuni tratti comuni, spesso la prossimità in base a una misura di distanza definita.
Oltre al termine data clustering (o semplicemente clustering), ci sono un certo numero di termini con significati simili, tra cui l’analisi dei cluster, la classificazione automatica, la tassonomia numerica, la botriologia e l’analisi tipologica.
- Tipi di clustering
- Clustering gerarchico
- Misura della distanza
- Creazione di cluster
- Clustering gerarchico agglomerativo
- Clustering partizionale
- k-means e derivati
- K-means clustering
- Algoritmo QT Clust
- Fuzzy c-significa clustering
- Criterio del gomito
- clustering
- Applicazioni
- Biologia
- Ricerche di mercato
- Altre applicazioni
- Confronti tra clustering di dati
- Vedi anche
- Bibliografia
- implementazioni del Software
- Gratis
Tipi di clustering
Gli algoritmi di clustering dei dati possono essere gerarchici o partizionali. Gli algoritmi gerarchici trovano cluster successivi utilizzando cluster precedentemente stabiliti, mentre gli algoritmi partizionali determinano tutti i cluster contemporaneamente. Gli algoritmi gerarchici possono essere agglomerati (dal basso verso l’alto) o divisivi (dall’alto verso il basso). Gli algoritmi agglomerativi iniziano con ogni elemento come un cluster separato e li uniscono in cluster successivamente più grandi. Gli algoritmi divisivi iniziano con l’intero set e procedono a dividerlo in cluster successivamente più piccoli.
Clustering gerarchico
Misura della distanza
Un passaggio chiave in un clustering gerarchico consiste nel selezionare una misura della distanza. Una misura semplice è la distanza di manhattan, uguale alla somma delle distanze assolute per ogni variabile. Il nome deriva dal fatto che in un caso a due variabili, le variabili possono essere tracciate su una griglia che può essere paragonata alle strade della città, e la distanza tra due punti è il numero di blocchi che una persona camminerebbe.
Una misura più comune è la distanza euclidea, calcolata trovando il quadrato della distanza tra ogni variabile, sommando i quadrati e trovando la radice quadrata di quella somma. Nel caso a due variabili, la distanza è analoga a trovare la lunghezza dell’ipotenusa in un triangolo; cioè, è la distanza “in linea d’aria.”Una revisione dell’analisi dei cluster nella ricerca sulla psicologia della salute ha rilevato che la misura della distanza più comune negli studi pubblicati in quell’area di ricerca è la distanza euclidea o la distanza euclidea quadrata.
Creazione di cluster
Data una misura della distanza, gli elementi possono essere combinati. Il clustering gerarchico crea (agglomerativo) o suddivide (divisivo) una gerarchia di cluster. La rappresentazione tradizionale di questa gerarchia è una struttura dati ad albero (chiamata dendrogramma), con singoli elementi a un’estremità e un singolo cluster con ogni elemento all’altra. Gli algoritmi agglomerativi iniziano nella parte superiore dell’albero, mentre gli algoritmi divisivi iniziano nella parte inferiore. (Nella figura, le frecce indicano un clustering agglomerativo.)
Tagliare l’albero ad una data altezza darà un clustering ad una precisione selezionata. Nell’esempio seguente, il taglio dopo la seconda riga produrrà cluster {a} {b c} {d e} {f}. Il taglio dopo la terza riga produrrà cluster {a} {b c} {d e f}, che è un clustering più grossolano, con un numero inferiore di cluster più grandi.
Clustering gerarchico agglomerativo
Ad esempio, supponiamo che questi dati debbano essere raggruppati. Dove la distanza euclidea è la metrica della distanza.
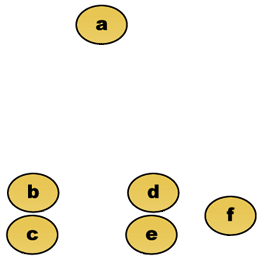
Dati grezzi
Il dendrogramma di clustering gerarchico sarebbe come tale:
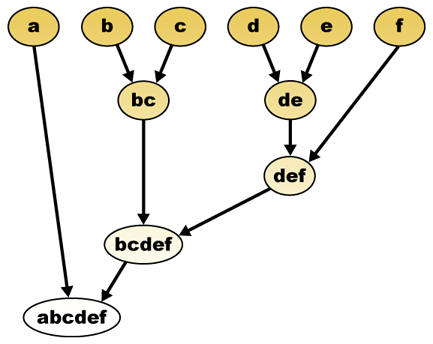
Rappresentazione tradizionale
Questo metodo costruisce la gerarchia dai singoli elementi unendo progressivamente i cluster. Di nuovo, abbiamo sei elementi {a} {b} {c} {d} {e} e {f}. Il primo passo è determinare quali elementi unire in un cluster. Di solito, vogliamo prendere i due elementi più vicini, quindi dobbiamo definire una distanza 
Supponiamo di aver unito i due elementi più vicini b e c, ora abbiamo i seguenti cluster {a}, {b, c}, {d}, {e} e {f} e vogliamo unirli ulteriormente. Ma per farlo, dobbiamo prendere la distanza tra {a} e {b c}, e quindi definire la distanza tra due cluster. Di solito la distanza tra due cluster 
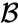
- La distanza massima tra gli elementi di ogni cluster (chiamato anche complete linkage clustering):
- La distanza minima tra gli elementi di ogni cluster (anche chiamato single linkage clustering):
- La distanza media tra gli elementi di ciascun cluster (chiamato anche media linkage clustering):
- La somma di tutte intra-cluster varianza
- L’aumento della varianza per il cluster, che sono state unite (Rione criterio)
- La probabilità che il candidato cluster di uova da la stessa funzione di distribuzione (V-linkage)
Ogni agglomerato si verifica a una maggiore distanza tra i cluster rispetto al precedente agglomerazione, e si può decidere di interrompere il clustering quando il cluster sono troppo distanti per essere uniti (criterio della distanza) o quando c’è un numero sufficientemente piccolo di cluster (criterio del numero).
Clustering partizionale
k-means e derivati
K-means clustering
L’algoritmo K-means assegna ogni punto al cluster il cui centro (chiamato anche centroide) è più vicino. Il centro è la media di tutti i punti del cluster, ovvero le sue coordinate sono la media aritmetica per ogni dimensione separatamente su tutti i punti del cluster.
Esempio: Il set di dati ha tre dimensioni e il cluster ha due punti: X = (x1, x2, x3) e Y = (y1, y2, y3). Quindi il centroide Z diventa Z = (z1, z2, z3), dove z1 = (x1 + y1)/2 e z2 = (x2 + y2)/2 e z3 = (x3 + y3)/2.
L’algoritmo è approssimativamente (J. MacQueen, 1967):
- Generare casualmente k cluster e determinare i centri di cluster, o direttamente generare k punti seme come centri di cluster.
- Assegna ogni punto al centro cluster più vicino.
- Ricalcola i nuovi centri cluster.
- Ripeti fino a quando non viene soddisfatto un criterio di convergenza (di solito che l’assegnazione non è cambiata).
I principali vantaggi di questo algoritmo sono la sua semplicità e velocità che gli consente di funzionare su set di dati di grandi dimensioni. Il suo svantaggio è che non produce lo stesso risultato ad ogni esecuzione, poiché i cluster risultanti dipendono dalle assegnazioni casuali iniziali. Massimizza la varianza inter-cluster (o minimizza la varianza intra-cluster), ma non garantisce che il risultato abbia un minimo globale di varianza.
Algoritmo QT Clust
Il clustering QT (Quality Threshold) (Heyer et al, 1999) è un metodo alternativo di partizionamento dei dati, inventato per il clustering dei geni. Richiede più potenza di calcolo di k-means, ma non richiede di specificare il numero di cluster a priori e restituisce sempre lo stesso risultato quando viene eseguito più volte.
L’algoritmo è:
- L’utente sceglie un diametro massimo per i cluster.
- Crea un cluster candidato per ogni punto includendo il punto più vicino, il prossimo più vicino e così via, fino a quando il diametro del cluster supera la soglia.
- Salvare il cluster candidato con il maggior numero di punti come primo cluster vero e rimuovere tutti i punti nel cluster da ulteriore considerazione.
- Ricorre con l’insieme ridotto di punti.
La distanza tra un punto e un gruppo di punti viene calcolata utilizzando il collegamento completo, ovvero come la distanza massima dal punto a qualsiasi membro del gruppo (vedere la sezione “clustering gerarchico agglomerativo” sulla distanza tra i cluster).
Fuzzy c-significa clustering
Nel clustering fuzzy, ogni punto ha un grado di appartenenza ai cluster, come nella logica fuzzy, piuttosto che appartenere completamente a un solo cluster. Pertanto, i punti sul bordo di un cluster possono trovarsi nel cluster in misura minore rispetto ai punti al centro del cluster. Per ogni punto x abbiamo un coefficiente che dà il grado di essere nel cluster kth 

Con fuzzy c-means, il centroide di un cluster è la media di tutti i punti, ponderata dal loro grado di appartenenza al cluster:
Il grado di appartenenza è correlato con l’inverso della distanza al cluster
i coefficienti sono normalizzati e fuzzyfied con un parametro reale 
Per m pari a 2, questo equivale a normalizzare linearmente il coefficiente per fare la loro somma 1. Quando m è vicino a 1, quindi centro cluster più vicino al punto è dato molto più peso rispetto agli altri, e l’algoritmo è simile a k-mezzi.
L’algoritmo fuzzy c-means è molto simile all’algoritmo k-means:
- Scegli un numero di cluster.
- Assegna casualmente a ciascun punto coefficienti per essere nei cluster.
- Ripeti fino a quando l’algoritmo non è convergente (cioè, la variazione dei coefficienti tra due iterazioni non è superiore a
, la soglia di sensibilità data) :
- Calcola il centroide per ogni cluster, usando la formula sopra.
- Per ogni punto, calcola i suoi coefficienti di essere nei cluster, usando la formula sopra.
L’algoritmo minimizza anche la varianza intra-cluster, ma ha gli stessi problemi di k-means, il minimo è un minimo locale e i risultati dipendono dalla scelta iniziale dei pesi.
Criterio del gomito
Il criterio del gomito è una regola empirica comune per determinare quale numero di cluster deve essere scelto, ad esempio per k-means e clustering gerarchico agglomerativo.
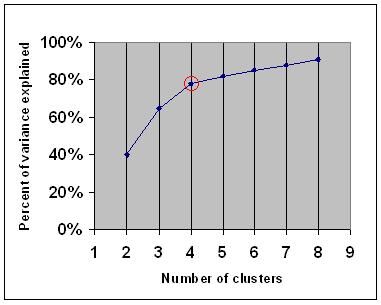
Il criterio elbow dice che dovresti scegliere un numero di cluster in modo che l’aggiunta di un altro cluster non aggiunga informazioni sufficienti. Più precisamente, se si traccia la percentuale di varianza spiegata dai cluster rispetto al numero di cluster, i primi cluster aggiungeranno molte informazioni (spiegano molta varianza), ma ad un certo punto il guadagno marginale diminuirà, dando un angolo nel grafico (il gomito).
Nel grafico seguente, il gomito è indicato dal cerchio rosso. Il numero di cluster scelti dovrebbe quindi essere 4.
clustering
Dato un insieme di punti dati, la somiglianza matrice può essere definita come una matrice 


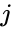
Una di queste tecniche è l’algoritmo Shi-Malik, comunemente usato per la segmentazione delle immagini. È partizioni punti in due set 
di 
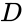
Questo partizionamento può essere fatto in vari modi, ad esempio prendendo la mediana 

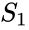
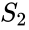
Un algoritmo correlato è l’algoritmo Meila-Shi, che prende gli autovettori corrispondenti agli autovalori k più grandi della matrice 
Applicazioni
Biologia
In biologia il clustering ha molte applicazioni nei campi della biologia computazionale e della bioinformatica, due delle quali sono:
- Nella trascrittomica, il clustering viene utilizzato per costruire gruppi di geni con modelli di espressione correlati. Spesso tali gruppi contengono proteine funzionalmente correlate, come enzimi per un percorso specifico, o geni che sono co-regolati. Gli esperimenti ad alto throughput che utilizzano tag di sequenza espressi (EST) o microarray di DNA possono essere un potente strumento per l’annotazione del genoma, un aspetto generale della genomica.
- Nell’analisi delle sequenze, il clustering viene utilizzato per raggruppare sequenze omologhe in famiglie geniche. Questo è un concetto molto importante nella bioinformatica e nella biologia evolutiva in generale. Vedi evoluzione per duplicazione genica.
Ricerche di mercato
L’analisi dei cluster è ampiamente utilizzata nelle ricerche di mercato quando si lavora con dati multivariati da sondaggi e pannelli di test. I ricercatori di mercato utilizzano l’analisi dei cluster per suddividere la popolazione generale dei consumatori in segmenti di mercato e per comprendere meglio le relazioni tra diversi gruppi di consumatori/potenziali clienti.
- Segmentare il mercato e determinare i mercati target
- Posizionamento del prodotto
- Sviluppo di nuovi prodotti
- Selezione dei mercati di prova (vedi : tecniche sperimentali)
Altre applicazioni
Analisi dei social network: nello studio dei social network, il clustering può essere utilizzato per riconoscere le comunità all’interno di grandi gruppi di persone.
Segmentazione dell’immagine: il clustering può essere utilizzato per dividere un’immagine digitale in regioni distinte per il rilevamento di bordi o il riconoscimento di oggetti.
Data mining: molte applicazioni di data mining comportano il partizionamento di elementi di dati in sottoinsiemi correlati; le applicazioni di marketing discusse sopra rappresentano alcuni esempi. Un’altra applicazione comune è la divisione di documenti, come le pagine World Wide Web, in generi.
Confronti tra clustering di dati
Ci sono stati diversi suggerimenti per una misura di somiglianza tra due clustering. Tale misura può essere utilizzata per confrontare quanto bene i diversi algoritmi di clustering dei dati eseguono su un insieme di dati. Molte di queste misure sono derivate dalla matrice corrispondente (aka confusion matrix), ad esempio, la misura Rand e le misure Fowlkes-Mallows Bk.
- Jain, Murty e Flynn: Data Clustering: Una recensione, ACM Comp. Surv., 1999. Disponibile qui.
- per un’altra presentazione di hierarchical, k-means e fuzzy c-means vedi questa introduzione al clustering. Ha anche una spiegazione sulla miscela di gaussiani.
- David Dowe, Pagina di modellazione della miscela – altri collegamenti di clustering e modello di miscela.
- un tutorial sul clustering
- Il libro di testo on-line: Information Theory, Inference, and Learning Algorithms, di David JC MacKay include capitoli su k-means clustering, soft k-means clustering e derivazioni tra cui l’algoritmo E-M e la visione variazionale dell’algoritmo E-M.
Vedi anche
- k-means
- rete neurale Artificiale (ANN)
- Self-organizing map
- Expectation Maximization (EM)
Bibliografia
- Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). L’uso e la segnalazione di cluster analysis in psicologia della salute: Una revisione. British Journal of Health Psychology 10: 329-358.
- Romesburg, H. Clarles, Cluster Analysis for Researchers, 2004, 340 pp. ISBN 1411606175 o editore, ristampa dell’edizione 1990 pubblicata da Krieger Pub. Co… Una traduzione in lingua giapponese è disponibile da Uchida Rokakuho Publishing Co., Ltd., Tokyo, Giappone.
- Heyer, LJ, Kruglyak, S. e Yooseph, S., Esplorando i dati di espressione:identificazione e analisi dei geni coespressi, Ricerca sul genoma 9: 1106-1115.
- Il libro di testo on-line: Information Theory, Inference, and Learning Algorithms, di David JC MacKay include capitoli su k-means clustering, soft k-means clustering e derivazioni tra cui l’algoritmo E-M e la visione variazionale dell’algoritmo E-M.
Per il clustering spettrale :
- Jianbo Shi e Jitendra Malik, “Normalized Cuts and Image Segmentation”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8), 888-905, August 2000. Disponibile sulla homepage di Jitendra Malik
- Marina Meila e Jianbo Shi, “Learning Segmentation with Random Walk”, Neural Information Processing Systems, NIPS, 2001. Disponibile dalla homepage di Jianbo Shi
Per stimare il numero di cluster:
- Can, F., Ozkarahan, E. A. (1990) “Concepts and effectiveness of the cover coefficient-based clustering methodology for text databases.”Transazioni ACM su sistemi di database. 15 (4) 483-517.
implementazioni del Software
Gratis
- il flexclust pacchetto per R
- YALE (Ancora un Altro Ambiente di Apprendimento): gratuito e open source software per il knowledge discovery e data mining anche un plugin per il clustering
- un po ‘ di Matlab file di origine per il clustering qui
- COMPACT – Comparativa Pacchetto per il Clustering di Valutazione (anche in Matlab)
- mixmod : Cluster basato su modelli e analisi discriminante. Codice in C++, interfaccia con Matlab e Scilab
- LingPipe Clustering Tutorial Tutorial per fare clustering completo e single – link utilizzando LingPipe, un pacchetto di data mining di testo Java distribuito con sorgente.
- Weka: Weka contiene strumenti per la pre-elaborazione dei dati, la classificazione, la regressione, il clustering, le regole di associazione e la visualizzazione. È anche adatto per lo sviluppo di nuovi schemi di apprendimento automatico.