Secondo Noam Chomosky, ci sono quattro tipi di grammatiche di Tipo 0, Tipo 1, tipo 2 e Tipo 3. La seguente tabella mostra come essi differiscono l’uno dall’altro−
| Grammatica di Tipo | Grammatica Accettato | Lingua Accettata | Automa |
|---|---|---|---|
| Tipo 0 | Illimitato di grammatica | Ricorsivamente enumerabile lingua | Macchina di Turing |
| Tipo 1 | sensibile al Contesto grammatica | sensibile al Contesto lingua | Lineari-delimitata automa |
| di Tipo 2 | grammatica libera dal Contesto, | Context-free language | Pushdown automa |
| Tipo 3 | Grammatica regolare | Linguaggio regolare | Automa a stati finiti |
Dai un’occhiata alla seguente illustrazione. Mostra l’ambito di ogni tipo di grammatica –
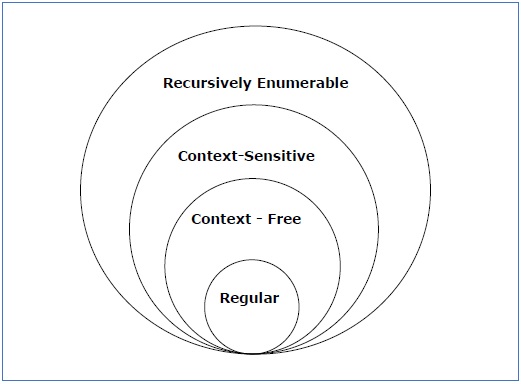
Grammatica di tipo 3
Le grammatiche di tipo 3 generano lingue regolari. Le grammatiche di tipo 3 devono avere un singolo non terminale sul lato sinistro e un lato destro costituito da un singolo terminale o da un singolo terminale seguito da un singolo non terminale.
Le produzioni devono essere nella forma X → a o X → aY
dove X, Y N N (Non terminale)
e a T T (Terminale)
La regola S → ε è consentita se S non appare sul lato destro di nessuna regola.
Esempio
X → ε X → a | aYY → b
Grammatica di tipo 2
Le grammatiche di tipo 2 generano linguaggi liberi dal contesto.
Le produzioni devono essere nella forma A → γ
dove A N N (Non terminale)
e γ γ (T N N)* (Stringa di terminali e non terminali).
Questi linguaggi generati da queste grammatiche sono riconosciuti da un automa pushdown non deterministico.
Esempio
S → X a X → a X → aX X → abc X → ε
Grammatica di tipo 1
Le grammatiche di tipo 1 generano linguaggi sensibili al contesto. Le produzioni devono essere nella forma
α A β → α γ β
dove A N N (non terminale)
e α, β, γ γ (T N N)* (Stringhe di terminali e non terminali)
Le stringhe α e β possono essere vuote, ma γ deve essere non vuota.
La regola S → ε è consentita se S non appare sul lato destro di nessuna regola. Le lingue generate da queste grammatiche sono riconosciute da un automa lineare limitato.
Esempio
AB → AbBc A → bcA B → b
Grammatica di tipo 0
Le grammatiche di tipo 0 generano linguaggi enumerabili ricorsivamente. Le produzioni non hanno restrizioni. Sono qualsiasi grammatica di struttura di fase comprese tutte le grammatiche formali.
Generano i linguaggi riconosciuti da una macchina di Turing.
Le produzioni possono essere sotto forma di α → β dove α è una stringa di terminali e non terminali con almeno un non terminale e α non può essere nullo. β è una stringa di terminali e non terminali.
Esempio
S → ACaB Bc → acB CB → DB aD → Db