CIRCONFÉRENCE ET COMMENT TROUVER
Il existe plusieurs façons de trouver la circonférence du tuyau et du tube rond. Connaître la circonférence est la clé de la construction de modèles précis à utiliser avec un tuyau. Plus vos chiffres sont précis lors du développement de ces modèles, meilleur sera votre ajustement. Comme pour tout, la pratique et l’expérience dans la création de modèles augmenteront également la précision.
La méthode la plus utilisée pour déterminer la circonférence utilise la formule du diamètre Pi x. Le tube rond de 6 po a une circonférence de 18,85 po. 6″ x Pi = 18,85″. Quand il s’agit de travailler avec un tuyau, vous devez savoir que le tuyau est mesuré nominalement. Cela signifie que le tuyau de 6 » n’est pas de 6″ OD. Heureusement, tous les fabricants de tuyaux suivent une norme et il existe un nombre incalculable de tableaux et de graphiques qui répertorient toutes les tailles de tuyaux et incluent même la circonférence de toutes les tailles! Veuillez vous référer à index pour trouver ces tableaux, graphiques et autres informations.
Au cours des prochaines sections, nous commencerons à développer des modèles à utiliser avec pipe. Peu importe la complexité du modèle, plusieurs concepts clés sont utilisés avec chacun d’eux, y compris la détermination de la circonférence. Nous ne présenterons ces concepts en détail qu’une seule fois, si vous avez besoin d’aide, veuillez vous référer à une section antérieure.
Nous parlerons de diviser la circonférence du tuyau en plusieurs parties égales qui aideront à développer le gabarit. Nous appellerons ces lignes des lignes d’éléments. Plus vous avez de lignes d’éléments, plus l’ajustement est précis.
Comme cela a été dit précédemment, les artisans ont trouvé de nombreuses façons de trouver des solutions à des problèmes complexes, c’est un livre qui en propose un.
Ci-dessous, nous avons un tuyau de 4 « . En se référant au tableau, nous pouvons voir que la DO de ce tuyau est de 4,50 « . Également sur le graphique, nous voyons qu’il a une circonférence totale de 14.125 « . Pour ce livre, nous allons diviser toutes les circonférences en 16 espaces égaux dans lesquels deviendront les lignes d’éléments. Le tableau pratique au dos nous montre également l’espacement pour diviser la circonférence en 16 parties, ainsi que 12, 8, 6, 4 et 2. N’oubliez pas que plus vous avez de lignes d’éléments, plus votre modèle sera précis. Si nous n’avions pas le graphique, vous deviez diviser la circonférence totale par le nombre d’espaces nécessaires. Un certain arrondi sera nécessaire pour ce faire, mais vous devez être conscient que le fait d’être 1/16 « , 16 fois finira par être désactivé par un 1″complet.
Si vous divisez 14,125 par 16, vous vous retrouvez à.883. Le graphique à l’état arrière.875. .875, ou 7/8 » est beaucoup plus facile à travailler sur un ruban à mesurer que.883. La différence est d’environ 1/132 par ligne, ce sera acceptable.
Pour commencer, nous allons dessiner une vue latérale qui montrera la hauteur de notre section de tuyau. Ensuite, nous devons dessiner dans notre étirement. Nous savons que la circonférence est de 14,125. Nous pouvons dessiner une verticale adjacente à la vue latérale d’un tuyau, puis étendre les lignes horizontales (indiquées en rouge) qui sont les lignes supérieure et inférieure de la vue latérale pour établir la hauteur totale du tuyau et les exécuter sur une longueur de 14.125 « . Une fois la hauteur et l’étirement terminés, nous sommes prêts à placer les lignes d’éléments.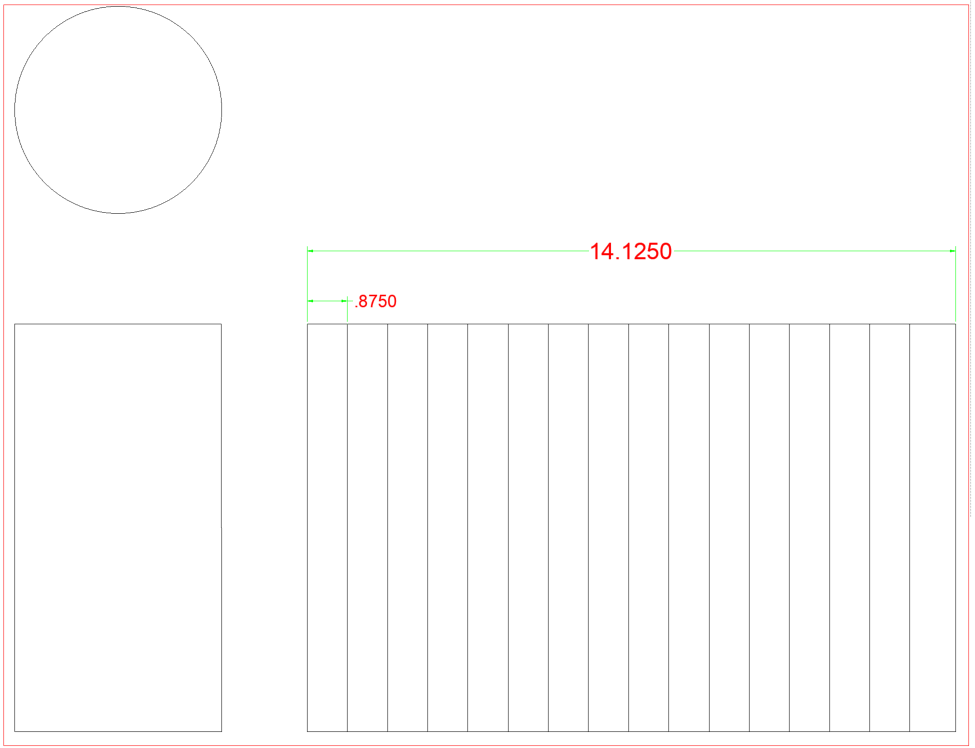
Lorsque vous travaillez avec des tuyaux et développez des modèles, vous devrez améliorer la géométrie de base et la bissection des angles. Nous utiliserons une boussole pour cette tâche.
Ci-dessous, nous avons une cabine d’angle avec un sommet du point A.
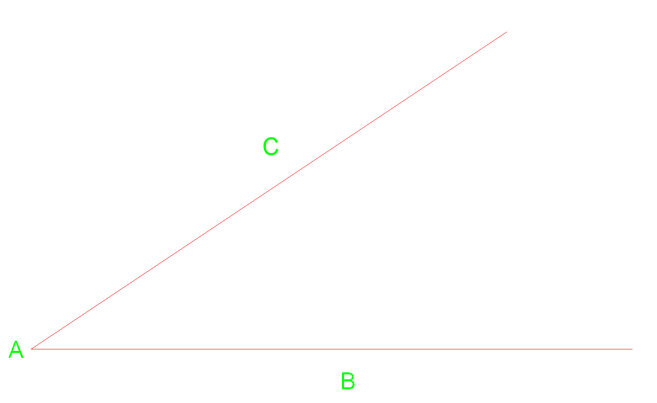
Nous pouvons d’abord dessiner un arc à partir du sommet A qui traverse la ligne près du point C & B. À partir de ces deux intersections, nous pouvons ensuite dessiner deux arcs supplémentaires vers la droite.
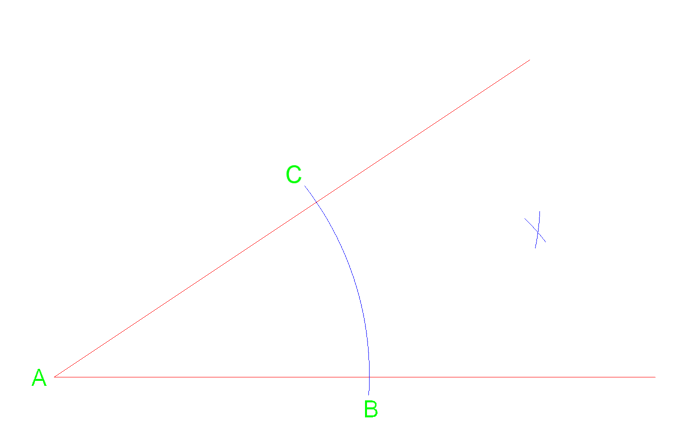
À partir du sommet A, tracez une ligne qui se croise au point D où l’arc se croise.
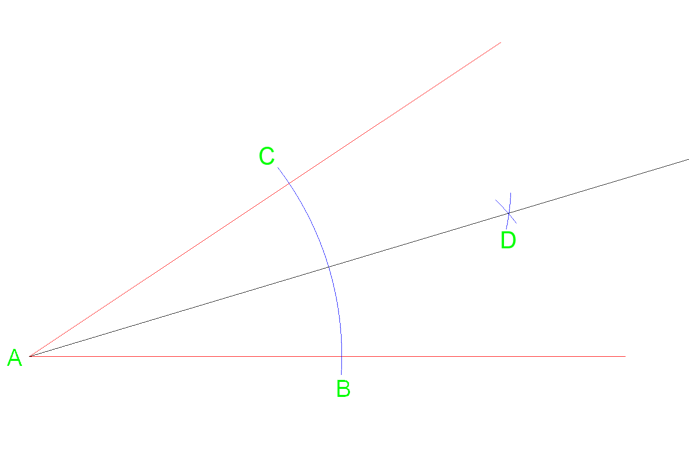
L’utilisation de cette méthode divisera également l’angle en deux angles de la même mesure. Cette méthode et peut être répétée si nécessaire pour la diviser à nouveau en 4 parties égales.
Essayons une méthode similaire sur un cercle. Le cercle dessiné a un diamètre de 3″ donc un rayon de 1 ½ ».
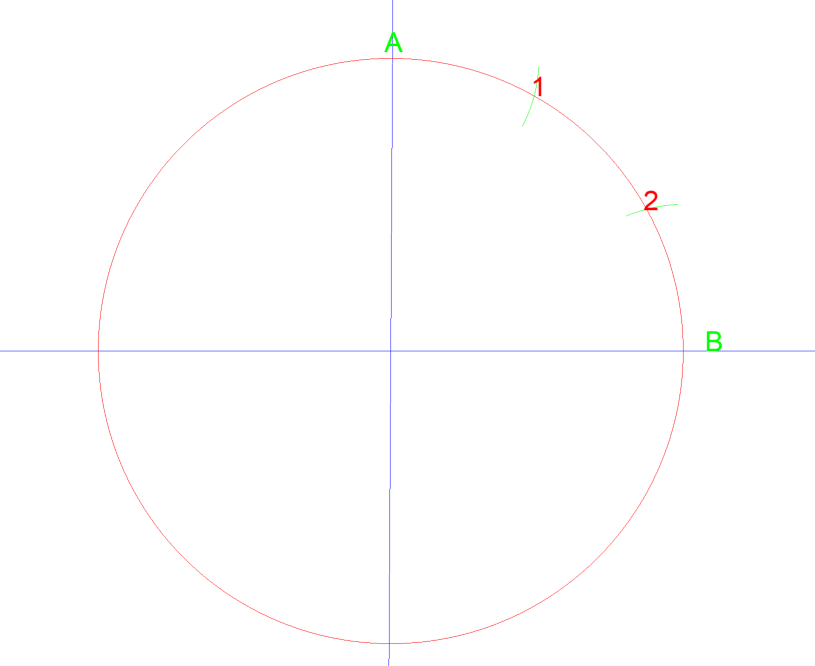
En réglant votre boussole sur le rayon du cercle, 1 ½ « , puis en dessinant un arc à partir du point A, puis B, ils se coupent à 1 & 2. Si vous tracez ensuite une ligne du centre du cercle à chaque point, vous venez de diviser ce quart de cercle en trois parties égales. Voir ci-dessous…
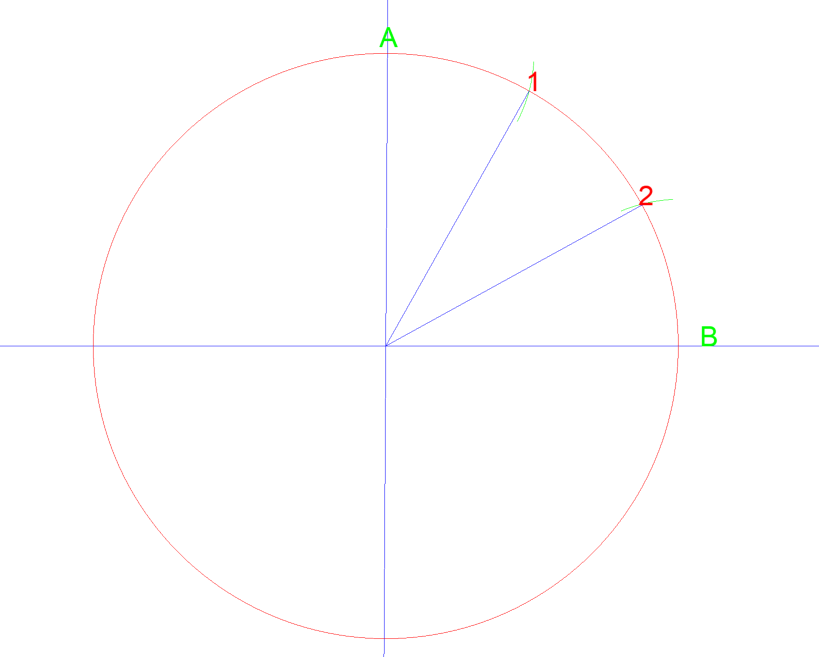
Si vous avez ensuite recommencé entre A, 1, 2, & B, vous pouvez diviser ce quart de cercle en 6 zones égales.
Comme nous l’avons couvert brièvement plus tôt, nous utilisons des chiffres pour aider à déterminer où les lignes se connecteront. Ces lignes seront utilisées lorsque nous assemblons deux pièces ou plus pour en faire un seul assemblage. Au fur et à mesure, vous comprendrez mieux comment fonctionne ce système de numérotation.