omkreds og hvordan man finder
der er et par måder at finde omkredsen af rør og runde rør. At kende omkredsen er nøglen til at opbygge nøjagtige skabeloner til brug med rør. Jo mere nøjagtige dine tal er, når du udvikler denne skabelon, jo bedre pasform har du. Som med alt andet vil praksis og erfaring med at opbygge skabeloner også øge nøjagtigheden.
den mest anvendte metode til at regne omkreds er ved hjælp af formlen for Pi diameter. 6 “od runde rør har en omkreds på 18,85″. 6″Pi=18,85”. Når det kommer til at arbejde med rør, skal du være opmærksom på, at rør måles nominelt. Det betyder, at 6 “rør er ikke 6” OD. Heldigvis, alle rørproducenter følger en standard, og der er et utal af tabeller og diagrammer, der viser alle rørstørrelser og endda inkluderer omkredsen i alle størrelser! Se indeks for at finde disse tabeller, diagrammer og andre oplysninger.
i løbet af de næste flere sektioner vil vi begynde at udvikle skabeloner til brug med rør. Uanset kompleksiteten af skabelonen er der flere nøglebegreber, der bruges sammen med dem alle, herunder bestemmelse af omkredsen. Vi vil kun introducere disse begreber i detaljer en gang, hvis du har brug for hjælp henvises tilbage til en tidligere afsnit.
vi vil tale om at opdele rørets omkreds i flere lige store dele, der vil hjælpe med at udvikle skabelonen. Vi vil henvise til disse linjer som elementlinjer. Jo flere elementlinjer du har, jo mere præcis passer.
som det blev sagt tidligere, er der mange måder, som håndværkere har fundet ud af løsninger på komplekse problemer, Dette er bog tilbyder en af dem.
nedenfor har vi nogle 4 ” rør. Ved at henvise til diagrammet kan vi se, at OD af dette rør er 4,50″. Også på diagrammet ser vi, at det har en samlet omkreds på 14.125″. For denne bog vil vi opdele alle omkredse i 16 lige store rum, hvor elementlinjerne bliver. Det praktiske diagram bagpå viser os også afstanden til opdeling af omkreds i 16 dele såvel som 12, 8, 6, 4 og 2. Husk, at jo flere elementlinjer du har, jo mere præcis bliver din skabelon. Hvis vi ikke havde diagrammet, skulle du dele den samlede omkreds med antallet af nødvendige mellemrum. Nogle afrunding vil være påkrævet, når du gør dette, men du skal være opmærksom på at være slukket 1/16″, 16 gange vil ende med at blive slukket af en fuld 1″.
hvis du deler 14.125 med 16 du ender på .883. Diagrammet i ryggen tilstand .875. .875, eller 7/8 ” er meget lettere at arbejde med på et målebånd end .883. Forskellen er omkring 1/132 pr.
for at komme i gang tegner vi et sidebillede, der viser højden på vores rørsektion. Næste skal vi trække i vores stretch-out. Vi ved, at omkredsen er 14.125. Vi kan tegne en lodret ved siden af et rør og derefter udvide de vandrette linjer (vist i rødt), der er de øverste og nederste linjer fra sidebillede for at fastslå rørets samlede højde og køre dem ud til en længde på 14.125″. Når vi har højden og udstrækningen færdig, er vi klar til at placere elementlinjerne.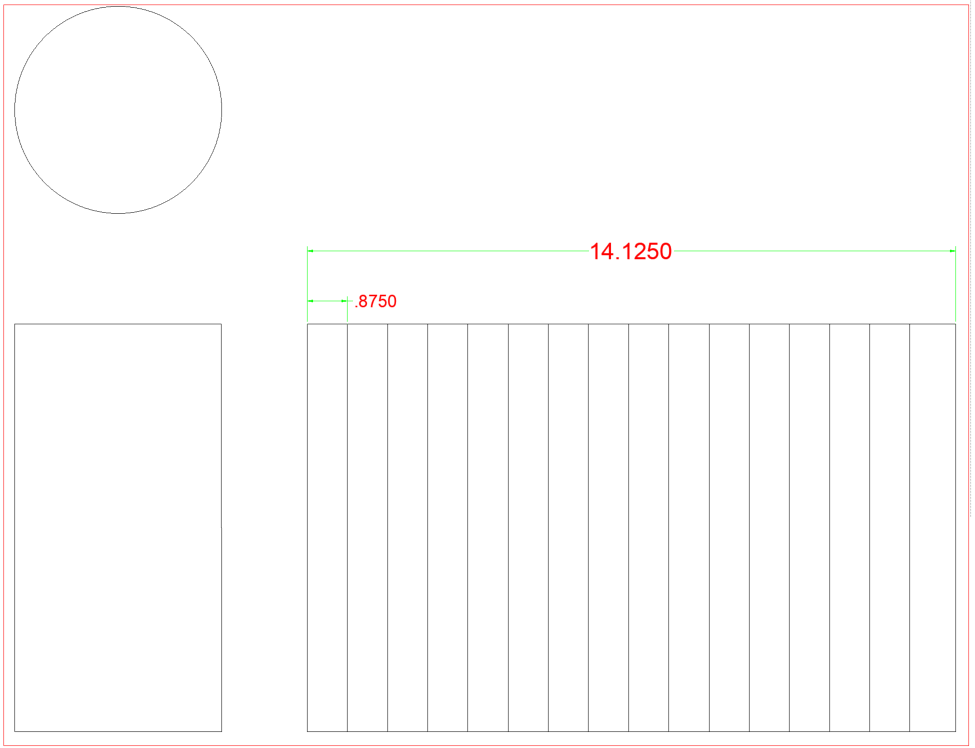
når du arbejder med rør og udvikler skabeloner, skal du børste op på nogle grundlæggende geometri og halvering af vinkler. Vi vil bruge et kompas til denne opgave.
nedenfor har vi vinkel førerhus med et toppunkt af punkt A.
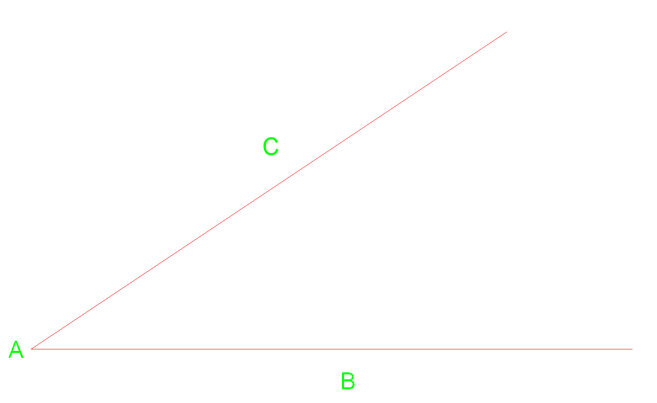
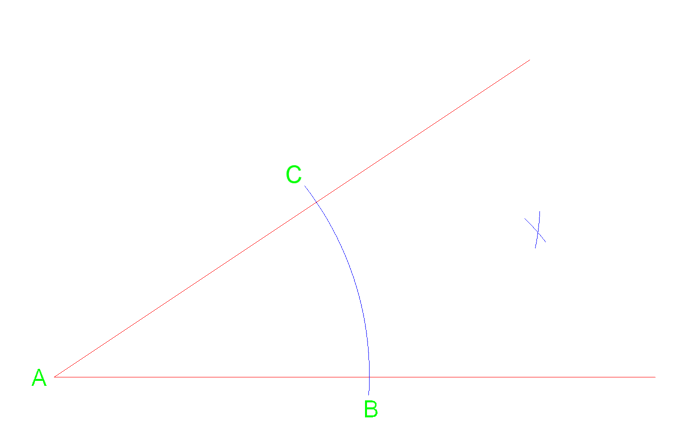
først kan vi tegne en bue fra toppunkt A, der krydser linjen nær punkt C & B. fra disse to kryds kan vi derefter tegne to yderligere buer til højre.
fra toppunkt en tegne en linje, der krydser ved punkt D, hvor buen skærer hinanden.
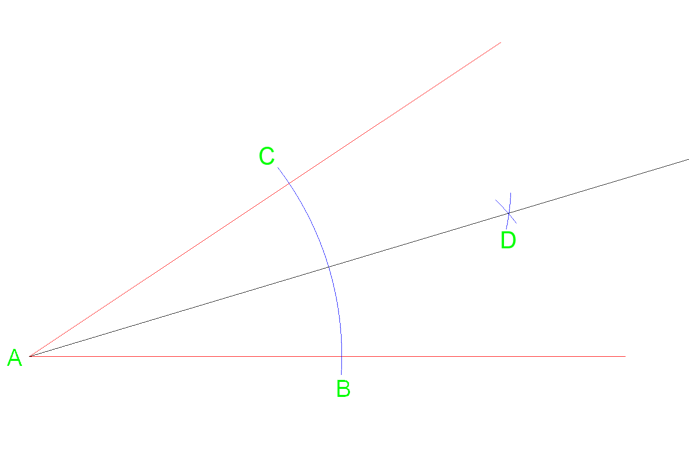
ved hjælp af denne metode vil ligeledes opdele vinklen i to vinkler af samme måling. Denne metode og kan gentages om nødvendigt for at opdele den igen i 4 lige store dele.
lad os prøve en lignende metode på en cirkel. Den tegnede cirkel har en diameter på 3″ så en radius på 1 liter”.
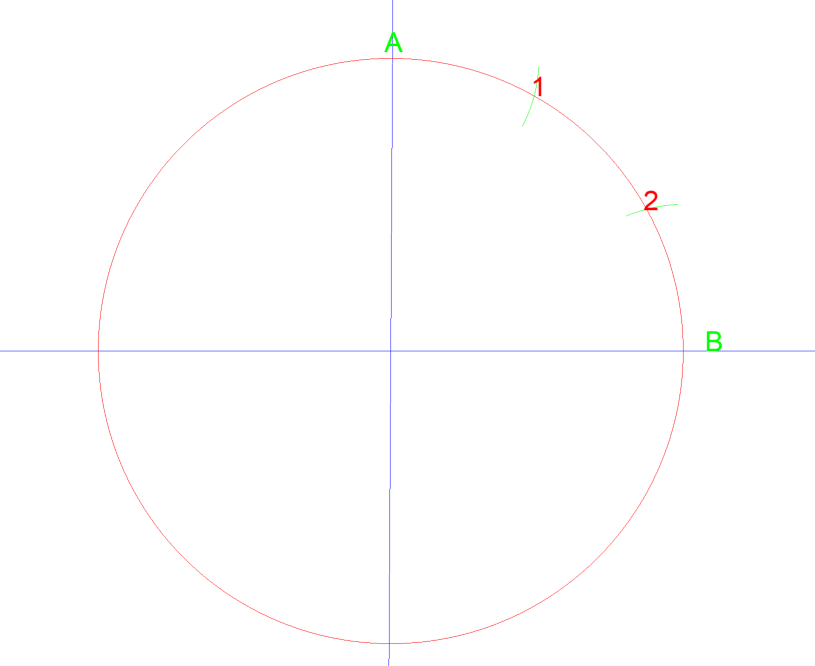
ved at indstille dit kompas til cirkelens radius, 1 liter” og derefter tegne en bue fra punkt A og derefter B skærer de ved 1 & 2. Hvis du derefter tegner en linje fra midten af cirklen til hvert punkt, delte du bare kvartalet af cirklen i tre lige store dele. Se nedenfor…
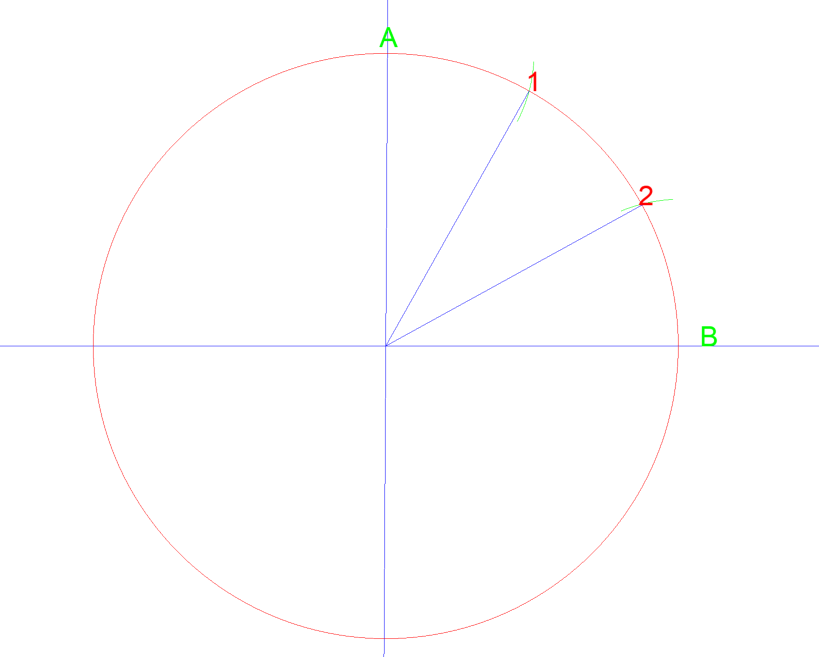
hvis du så gjorde dette igen mellem A, 1, 2, & B, kan du opdele kvartalet af en cirkel i 6 lige store områder.
som vi dækkede kort Tidligere, bruger vi Tal til at hjælpe med at oprette forbindelse til, hvor linjer vil forbinde. Disse linjer vil blive brugt, når vi forbinder to eller flere dele sammen for at lave en samling. Når vi fortsætter, vil du bedre forstå, hvordan dette nummereringssystem fungerer.