fdtd og FDM algoritmer til mhof-analysen
optisk lys er elektromagnetisk bølge i naturen, og dets formeringsegenskaber styres således af elektrodynamikens love, der kollektivt er kendt som Maksels ligninger. Det er kendt, at styring af lyssignaler i MHOF med fotoniske båndgapstrukturer er afhængig af konstruktiv interferenseffekt på grund af det periodiske arrangement af identiske lufthuller. På den anden side, når lufthullerne bliver tilfældige i størrelse, placering eller begge dele, finder fænomenet total intern refleksion sted, og indeksforskellen mellem kernen og beklædningen giver lysindeslutning og dermed vejledning af lys langs fiberen. Selvom formeringsegenskaberne for komplicerede strukturer som vilkårlige MHOFs ikke let kan beregnes ved hjælp af analysemetoder, er der måder at løse elektromagnetiske problemer numerisk.
i dette afsnit behandles to numeriske teknikker for finite-difference time-domain (FDTD) og finite difference method (FDM) i betragtning af udvidelse til analysen af holey optiske fibre med vilkårlige lufthulsfordelinger. Hver af disse teknikker har visse fordele. Ved hjælp af fdtd-metoden samples det kontinuerlige elektromagnetiske felt i et endeligt rumfang på forskellige punkter i et rumgitter og ved lige store prøveudtagningspunkter i tiden. De samplede data på punkterne bruges til numeriske beregninger af tilladte tilstande uden at generere falske tilstandsløsninger i en given bølgeleder. På trods af at det er en effektiv teknik til beregning af formeringskonstanter af guidede tilstande, er fdtd-metoden ikke velegnet til evaluering af individuelle tilstandsfeltfordelinger. Dette skyldes, at kilden er en impulsfunktion i tidsdomænet, der dækker et uendeligt spektrum, og derfor er feltfordelingsløsninger superposition af alle mulige tilstande. For at afhjælpe dette problem med formeringskonstanter, der er tilgængelige fra FDTD, opnås individuelle tilstandsfeltfordelinger ved hjælp af FDM, som hurtigt og bekvemt kan levere individuelle tilstandsfeltløsninger.
FDTD har vundet betydelig popularitet i de senere år, fordi denne metode giver robuste løsninger baseret på Maksels ligninger og let kan rumme komplekse værdsatte materialeegenskaber. Et vilkårligt materialeobjekt kan tilnærmes ved at opbygge enhedsceller, for hvilke feltkomponentpositioner er anbragt med de ønskede værdier for permittivitet og permeabilitet. Når objektets geometri er specificeret i det numeriske simuleringsregion, modelleres kildebetingelsen et eller andet sted i regionen. Oprindeligt antages det, at alle felter inden for beregningsdomænet er identisk nul. Derefter håndhæves en hændelsesbølge for at komme ind i det numeriske beregningsområde.
brug af MKS-systemet af enheder, lad os først overveje:
hvor List er den elektriske permittivitetskonstant i F/M og List er den magnetiske permeabilitetskonstant i H/M. udvidelse af Krølleudtryk og lignelse af lignende komponenter dannes systemet med seks koblede partielle differentialligninger til FDTD-analysen af elektromagnetiske bølgeinteraktioner med generelle tredimensionelle objekter. Det skal bemærkes, at de elektriske og magnetiske feltkomponenter (f.eks. Det vil sige, at Maksels ligninger ikke direkte giver elektriske og magnetiske feltværdier, men snarere relaterer ændringshastigheden mellem elektriske og magnetiske feltværdier.
vedtagelse af central endelig forskel tilnærmelse for rum – og tidsderivater med nøjagtighed til anden rækkefølge kan følgende tilnærmelser som repræsentative eksempler i en tredimensionel (3D) fdtd-formulering udvikles:
hvor i, j, k, og n er hele tal, for Δx, Δy, Δz, og Δt, som henholdsvis den plads og tid ad gangen .
da optiske fibre såsom MHOFs generelt ikke har nogen variationer langs udbredelsesretningen, og variationer af materialeegenskaber er begrænset til tværretningerne som vist i figur 3, kan 3D FDTD-formuleringen forenkles til den kompakte todimensionale (2D) FDTD-algoritme . Ved at bruge fasornotation med den aksiale formeringskonstant (kurr) erstattes de første ordens partielle derivater med hensyn til Å med-J kurr, fordi felternes afhængighed er som ekspr. Og to tilstødende felter, der kræves for førsteordensderivater i det diskretiserede rumområde, kan repræsenteres af et felt midt imellem dem. Baseret på disse to fakta opnås følgende formulering som et eksempel:
den resulterende 2D-algoritme drager fordel af en betydelig reduktion i den krævede computerhukommelsesallokering og driftstid. Således til computerberegning af vilkårlige bølgeledere, der er ensartede i retning af bølgeudbredelse, er kun modellering af tværsnittene af bølgeledere tilstrækkelig.
sammen med denne effektive algoritme skal uendelige medier i 2D-rummet til et vilkårligt elektromagnetisk objekt modelleres omhyggeligt, fordi computerhukommelsen er begrænset i beregningsområdet, selv med avanceret nuværende teknologi. For at modellere regioner, der strækker sig til uendelig, er et perfekt matchet lag (PML) som en meget effektiv absorberende grænsetilstand (ABC) designet ved den ydre gittergrænse for et beregningsdomæne. Ideelt set er det absorberende medium kun så tykt som et par gitterceller, stærkt absorberende, reflektionsløs for alle imponerende bølger og effektiv over hele spektret af driftsbølgelængder.
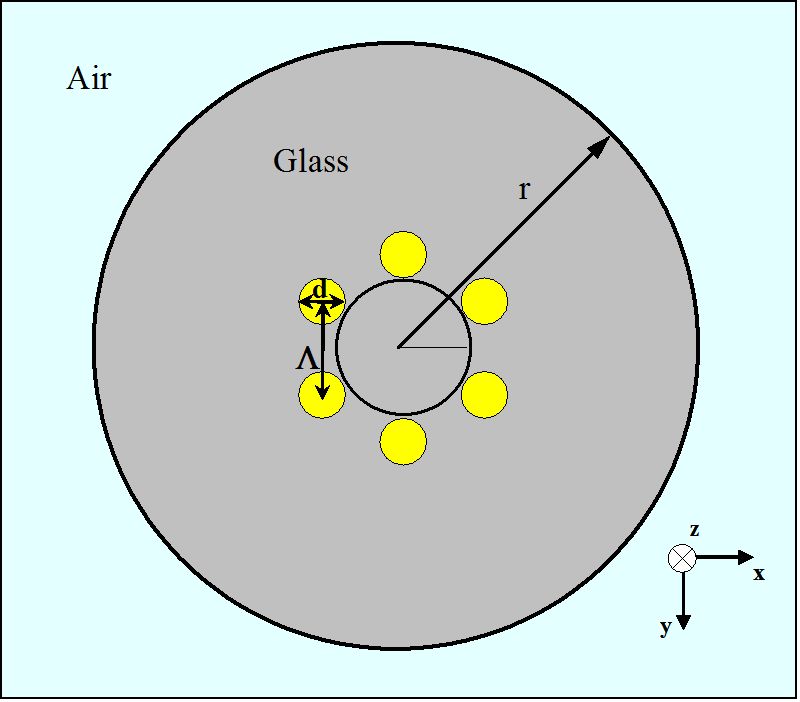
figur 3.
skematisk af et tværsnit for en MHOF med et lag lufthuller i et sekskantet arrangement
på samme måde som udviklingen af fdtd-algoritmen kan FDM-formuleringen udledes af den koblede Maksels ligninger . For kontinuerlige bølger i lineære og isotrope medier resulterer kombination af EKV ‘ er (2) og (3) i følgende vektorielle bølgeligning:
hvor n er brydningsindekset og k0 er formeringskonstanten i frit rum. Mange bølgeledere, som f.eks optiske fibre, kan ses som å-invariant, eller stykkevis å-invariant strukturer. For disse strukturer varierer brydningsindekset n langsomt langs udbredelsesretningen å, hvilket er gyldigt for de fleste fotoniske styrede bølgeenheder. Ved at bruge vektoridentiteten af∇×∇×=∇(∇⋅)−∇2, EKV (8)kan skrives som
også med den rimelige antagelse om ubetydelig tidsafhængighed langs å-aksen kan FDM-formuleringen som i EKV (9) implementeres ved at erstatte rumlige derivater med endelige forskel tilnærmelser. Her skal det bemærkes, at den tværgående del af (9)
hvor indeks “t” står for den tværgående komponenter. Da den langsgående komponent let kan opnås ved anvendelse af følgende nul divergens (Gauss lov) begrænsning:
de tværgående komponenter er tilstrækkelige til at beskrive det elektromagnetiske felts fulde vektorielle natur i en optisk bølgeleder.
til den indledende undersøgelse af vejledningsegenskaber for MHOFs er den optiske fiber vist i figur 3 computeranalyseret. Generelt kan mhof-geometrien beskrives med to parametre, stigningslængde (liter) og diameter (d), som angivet i figur 3. Her er stigningslængden afstanden mellem centre for to nærmeste lufthuller med den cylindriske form. For MHOF i figur 3 har hvert lille lufthul en diameter på 1,4 liter, hvilket udgør en sekskant med liter = 1,7 liter. Glasdelen omkring de seks lufthuller i de gule områder har et brydningsindeks på 1,45. Den ydre radius (r) af den holey fiber antages at være 10 liter. Også den udvendige region af MHOF er luft.
når tværsnittet af en holey fiber er defineret i et korrekt beregningsdomæne, kan fdtd-simuleringen udføres med flere specificerede parametre, såsom Krar ved definition af en Gaussisk kilde, Krar for stabil Simulering, det samlede antal (ntot) tidstrin til prøveudtagning af data i tidsdomænet og rimelige værdier af Krar. Her, for at undgå numerisk divergens og sikre stabiliteten af fdtd-algoritmen, skal der vælges en passende Krart for at tilfredsstille følgende stabilitetsbetingelse:
hvor cM er den maksimale bølgefasehastighed inden for en given numerisk model. Sammenfattende mekanismen bag fdtd-analysen fortsætter computersimuleringen med følgende trin:
-
Vælg passende parameterværdier (lp, lp, ntot og LP)
-
prøveudtagning af data for en feltkomponent i tidsdomænet
-
Tag Fourier-transformationen af tidsdataene
-
få spektrale data for en feltkomponent
-
vælg tilstandsfrekvenser, der er knyttet til lydstyrkeværdien
-
indsamle data om frekvens og tilstand
-
lav et plot af tilstandsindeks versus bølgelængde
figur 4 illustrerer de karakteristiske kurver, der opnås fra FDTD beregning, for de første tre lavere ordens tilstande af MHOF defineret i figur 3.
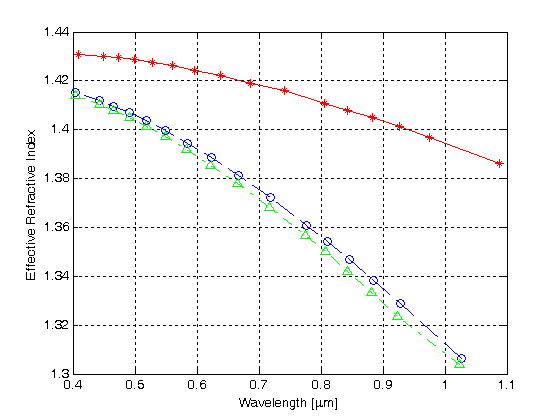
figur 4.
effektivt brydningsindeks versus bølgelængde for de første tre tilstande i en MHOF med et lag lufthuller
den røde kurve med stjernesymbolerne tegner den normaliserede formeringskonstant for den første tilstand versus bølgelængde, mens de blå og grønne kurver viser de normaliserede formeringskonstanter for henholdsvis den anden og den tredje tilstand. Resultaterne indikerer, at HMOF med et enkelt sekskantet lufthulsbeklædningslag understøtter multimodestyring.