ifølge Noam Chomosky er der fire typer grammatikker-Type 0, Type 1, Type 2 og Type 3. Følgende tabel viser, hvordan de adskiller sig fra hinanden−
| grammatik Type | grammatik accepteret | sprog accepteret | automat |
|---|---|---|---|
| Type 0 | ubegrænset grammatik | rekursivt enumerable sprog | Turing maskine |
| Type 1 | Kontekstfølsom grammatik | kontekstfølsomt sprog | lineær afgrænset automat |
| Type 2 | Kontekstfri grammatik | Kontekstfrit sprog | tryk ned automat |
| Type 3 | regulær grammatik | regulært sprog | Finite state automat |
se på følgende illustration. Det viser omfanget af hver type grammatik –
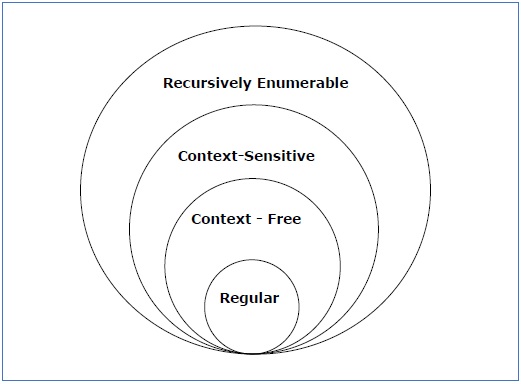
type – 3 grammatik
Type-3 grammatikker genererer almindelige sprog. Type 3-grammatikker skal have en enkelt ikke-terminal på venstre side og en højre side bestående af en enkelt terminal eller en enkelt terminal efterfulgt af en enkelt ikke-terminal.
produktionerne skal være i form af en eller en en
hvor en, en en n (ikke terminal)
og en en t (Terminal)
reglen er tilladt, hvis S ikke vises på højre side af en regel.
eksempel
X → ε X → a | aYY → b
type – 2 grammatik
Type-2 grammatikker genererer kontekstfrie sprog.
produktionerne skal være i form af en lyster
hvor en lyster n (ikke Terminal)
og lyster (t-lyster N)* (streng af terminaler og ikke-terminaler).
disse sprog genereret af disse grammatikker genkendes af en ikke-deterministisk push-ned-automat.
eksempel
S → X a X → a X → aX X → abc X → ε
type – 1 grammatik
type-1 grammatikker genererer kontekstfølsomme sprog. Produktionerne skal være i form
α En β → α γ β
, hvor A ∈ N (Non-terminal)
og α, β, γ ∈ (T ∪ N)* (Strenge af terminaler og non-terminaler)
strengene α og β kan være tom, men γ skal være ikke-tom.
reglen er tilladt, hvis S ikke vises på højre side af nogen regel. De sprog, der genereres af disse grammatikker, genkendes af en lineær afgrænset automat.
eksempel
AB → AbBc A → bcA B → b
Type – 0 grammatik
Type-0 grammatikker genererer rekursivt tællelige sprog. Produktionen har ingen begrænsninger. De er enhver fase struktur grammatik herunder alle formelle grammatikker.
de genererer de sprog, der genkendes af en Turing-maskine.
produktionerne kan være i form af KR., hvor kr. er en række terminaler og ikke-terminaler med mindst en ikke-Terminal, og KR. kan ikke være null. det er en række terminaler og ikke-terminaler.
Eksempel
S → ACaB Bc → acB CB → DB aD → Db