co je to klastrová analýza?
shluková analýza je průzkumná analýza, která se snaží identifikovat struktury uvnitř dat. Shluková analýza se také nazývá segmentační analýza nebo taxonomická analýza. Konkrétněji se snaží identifikovat homogenní skupiny případů, pokud seskupení není dříve známo. Protože je průzkumný, nerozlišuje mezi závislými a nezávislými proměnnými. Různé metody analýzy clusteru, které SPSS nabízí, mohou zpracovávat binární, nominální, pořadové a měřítko (interval nebo poměr) dat.
shluková analýza se často používá ve spojení s jinými analýzami(jako je diskriminační analýza). Výzkumný pracovník musí být schopen interpretovat klastrovou analýzu na základě jejich porozumění datům, aby zjistil, zda jsou výsledky analýzy skutečně smysluplné.
typické výzkumné otázky odpovědi na klastrovou analýzu jsou následující:
- medicína-jaké jsou diagnostické klastry? Chcete-li odpovědět na tuto otázku výzkumník by navrhnout diagnostický dotazník, který zahrnuje možné příznaky (například v psychologii, úzkost, deprese atd.). Klastrová analýza pak může identifikovat skupiny pacientů, kteří mají podobné příznaky.
- Marketing-jaké jsou segmenty zákazníků? Chcete-li odpovědět na tuto otázku výzkumník trhu může provést průzkum pokrývající potřeby, postoje, demografie a chování zákazníků. Výzkumník pak může použít klastrovou analýzu k identifikaci homogenních skupin zákazníků, kteří mají podobné potřeby a postoje.
- vzdělávání-jaké jsou studentské skupiny, které vyžadují zvláštní pozornost? Vědci mohou měřit psychologické, nadání, a charakteristiky úspěchu. Shluková analýza pak může určit, jaké homogenní skupiny existují mezi studenty (například vysoce úspěšní ve všech předmětech nebo studenti, kteří vynikají v určitých předmětech, ale v jiných selhávají).
- biologie-jaká je taxonomie druhů? Vědci mohou shromáždit soubor dat různých rostlin a zaznamenat různé atributy jejich fenotypů. Shluková analýza může tato pozorování seskupit do řady shluků a pomoci vybudovat taxonomii skupin a podskupin podobných rostlin.
další techniky, které byste mohli vyzkoušet, abyste identifikovali podobné skupiny pozorování, jsou Q-analýza, vícerozměrné škálování (MDS) a analýza latentní třídy.
shluková analýza v SPSS
naše výzkumná otázka pro tento příklad shlukové analýzy je následující:
jaké homogenní shluky studentů se objevují na základě standardizovaných výsledků testů v matematice, čtení a psaní?
v SPSS clusterové analýzy lze nalézt v analyzovat/klasifikovat…. SPSS nabízí tři metody pro analýzu klastru: klastr K-Means, hierarchický klastr a dvoustupňový klastr.
k-means cluster je metoda pro rychlé shlukování velkých datových sad. Výzkumný pracovník předem definuje počet klastrů. To je užitečné pro testování různých modelů s různým předpokládaným počtem klastrů.
hierarchický cluster je nejběžnější metodou. Generuje řadu modelů s clusterovými řešeními od 1 (všechny případy V jednom clusteru) do n (každý případ je individuální cluster). Hierarchický klastr také pracuje s proměnnými na rozdíl od případů; může seskupovat proměnné dohromady způsobem poněkud podobným faktorové analýze. Kromě toho může hierarchická klastrová analýza zpracovávat nominální, pořadová a měřítková data; nedoporučuje se však kombinovat různé úrovně měření.
dvoufázová analýza clusteru identifikuje seskupení nejprve spuštěním předběžného clusteru a poté spuštěním hierarchických metod. Vzhledem k tomu, že používá rychlý algoritmus clusteru předem, to zvládne velké datové sady, které by trvat dlouhou dobu pro výpočet s hierarchickými metodami clusteru. V tomto ohledu jde o kombinaci předchozích dvou přístupů. Dvoustupňové clustering zvládne měřítko a pořadová data ve stejném modelu, a to automaticky vybere počet clusterů.
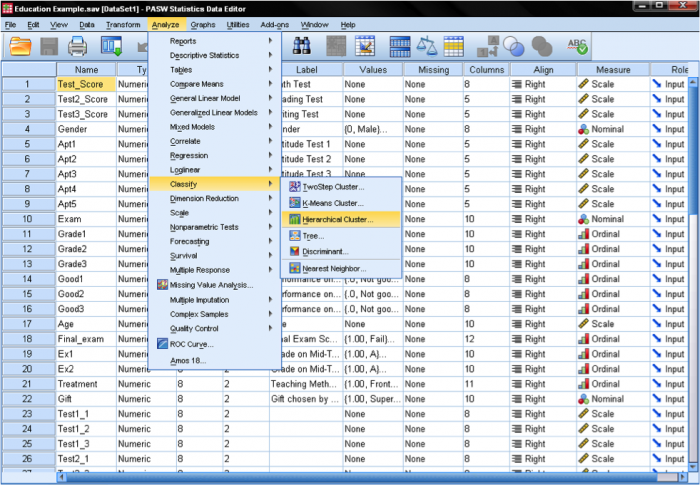
hierarchická analýza klastrů se řídí třemi základními kroky: 1) Vypočítejte vzdálenosti, 2) propojte klastry a 3) Vyberte řešení výběrem správného počtu klastrů.
nejprve musíme vybrat proměnné, na kterých zakládáme naše klastry. V dialogovém okně přidáme testy matematiky, čtení a zápisu do seznamu proměnných. Protože chceme shlukovat případy, ponecháme zbytek zaškrtnutí ve výchozím nastavení.
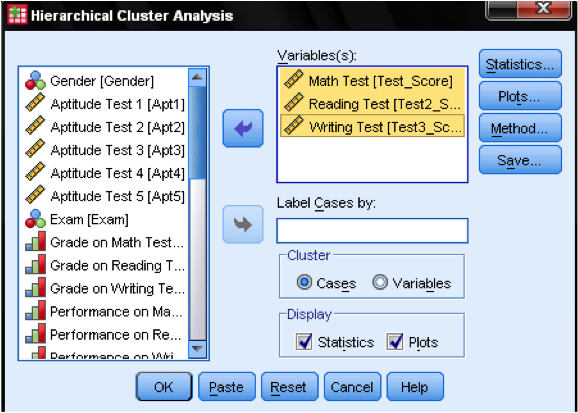
v dialogovém okně Statistika … můžeme určit, zda chceme v našich pozorováních výstup matice přiblížení (to jsou vzdálenosti vypočtené v prvním kroku analýzy) a předpokládané členství klastrů v případech. Opět ponecháme všechna nastavení ve výchozím nastavení.

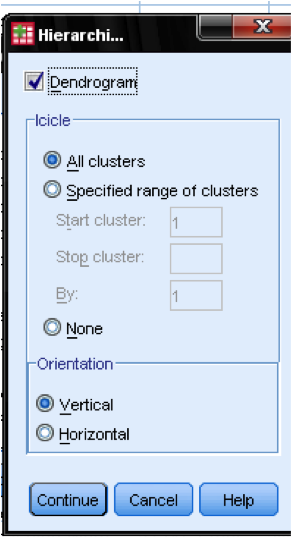
v dialogovém okně grafy … bychom měli přidat Dendrogram. Dendrogram graficky ukáže, jak jsou klastry sloučeny, a umožní nám určit, jaký je vhodný počet klastrů.
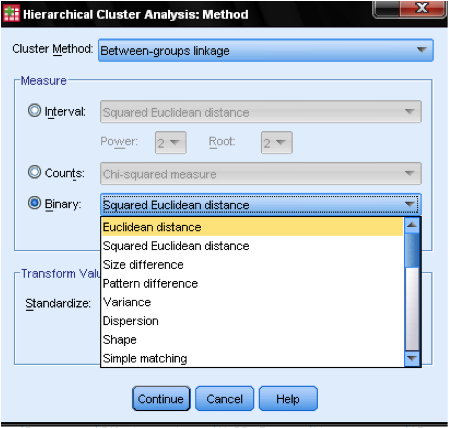
metoda dialogového okna … nám umožňuje určit míru vzdálenosti a metodu shlukování. Nejprve musíme definovat správné měření vzdálenosti. SPSS nabízí tři velké bloky měření vzdálenosti Pro interval (měřítko), počty (ordinální) a binární (nominální) data.
pro intervalová data je nejběžnější čtvercová euklidovská vzdálenost. Je založen na euklidovské vzdálenosti mezi dvěma pozorováními, což je druhá odmocnina součtu čtvercových vzdáleností. Vzhledem k tomu, že euklidovská vzdálenost je na druhou, zvyšuje význam velkých vzdáleností a zároveň oslabuje význam malých vzdáleností.

pokud máme pořadová data (počty), můžeme si vybrat mezi Chi-čtvercem nebo standardizovaným Chi-čtvercem zvaným Phi-čtverec. Pro binární data se běžně používá čtvercová euklidovská vzdálenost.

v našem příkladu zvolíme Interval a čtvercovou euklidovskou vzdálenost.
dále musíme zvolit metodu clusteru. Obvykle jsou volby mezi skupinami vazba (vzdálenost mezi shluky je průměrná vzdálenost všech datových bodů v těchto shlucích), nejbližší soused (jednoduchá vazba: vzdálenost mezi shluky je nejmenší vzdálenost mezi dvěma datovými body), nejvzdálenější soused (úplná vazba: vzdálenost je největší vzdálenost mezi dvěma datovými body) a Wardova metoda(vzdálenost je vzdálenost všech shluků k velkému průměru vzorku). Jednoduchá vazba funguje nejlépe s dlouhými řetězci shluků, zatímco úplná vazba funguje nejlépe s hustými kuličkami shluků. Propojení mezi skupinami funguje s oběma typy clusterů. Doporučuje se nejprve použít jednu vazbu. Ačkoli jediná vazba má tendenci vytvářet řetězce shluků, pomáhá při identifikaci odlehlých hodnot. Po vyloučení těchto odlehlých hodnot můžeme přejít na Wardovu metodu. Wardova metoda používá hodnotu F (jako v Anově) k maximalizaci významu rozdílů mezi klastry.
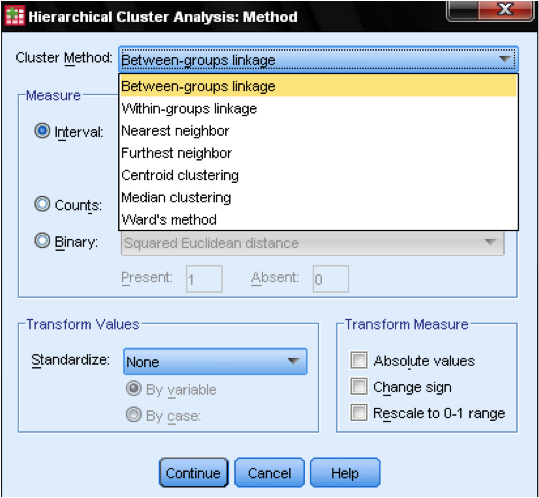
Poslední úvahou je standardizace. Pokud mají proměnné různé stupnice a znamená, že bychom mohli chtít standardizovat buď na skóre Z, nebo centrováním stupnice. Můžeme také transformovat hodnoty na absolutní hodnoty, pokud máme datovou sadu, kde by to mohlo být vhodné.