podle Noama Chomoskyho existují čtyři typy gramatik − Typ 0, typ 1, typ 2 a typ 3. Následující tabulka ukazuje, jak se navzájem liší−
| Typ gramatiky | gramatika přijata | jazyk přijat | automat |
|---|---|---|---|
| Typ 0 | neomezená gramatika | rekurzivně vyčíslitelný jazyk | Turingův stroj |
| typ 1 | kontextová gramatika | kontextový jazyk | lineárně ohraničený automat |
| typ 2 | bezkontextová gramatika | bezkontextový jazyk | Pushdown automat |
| typ 3 | regulární gramatika | regulární jazyk | konečný stavový automat |
podívejte se na následující obrázek. Ukazuje rozsah každého typu gramatiky –
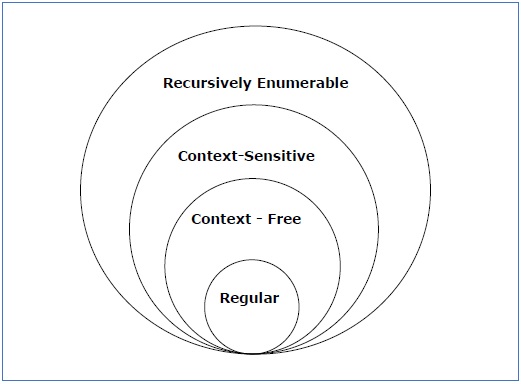
gramatika typu 3
gramatiky typu 3 generují regulární jazyky. Gramatiky typu 3 musí mít na levé straně jeden ne-terminál a na pravé straně sestávající z jednoho terminálu nebo jednoho terminálu následovaného jedním ne-terminálem.
produkce musí být ve tvaru X → a nebo X → aY
kde X, Y ∈ N (non terminal)
a a ∈ T (Terminal)
pravidlo s → ε je povoleno, pokud se S neobjeví na pravé straně žádného pravidla.
příklad
X → ε X → a | aYY → b
gramatika typu 2
gramatiky typu 2 generují bezkontextové jazyky.
produkce musí být ve tvaru a → γ
kde A ∈ N (neterminální)
a γ ∈ (T N N)* (řetězec svorek a neterminálů).
tyto jazyky generované těmito gramatikami jsou rozpoznávány nedeterministickým tlačným automatem.
příklad
S → X a X → a X → aX X → abc X → ε
gramatika typu 1
gramatiky typu 1 generují jazyky citlivé na kontext. Produkce musí být ve tvaru
α A β → α γ β
kde A ∈ N (neterminální)
a α, β, γ ∈ (T N N)* (řetězce terminálů a neterminálů)
řetězce α a β mohou být prázdné, ale γ musí být neprázdné.
pravidlo s → ε je povoleno, pokud se S neobjeví na pravé straně žádného pravidla. Jazyky generované těmito gramatikami jsou rozpoznávány lineárním ohraničeným automatem.
příklad
AB → AbBc A → bcA B → b
gramatika typu 0
gramatiky typu 0 generují rekurzivně vyčíslitelné jazyky. Produkce nemají žádná omezení. Jedná se o gramatiku s fázovou strukturou včetně všech formálních gramatik.
generují jazyky, které jsou rozpoznány Turingovým strojem.
produkce může být ve formě α → β, kde α je řetězec terminálů a neterminálů s alespoň jedním neterminálem a α nemůže být null. β je řetězec terminálů a neterminálů.
Příklad
S → ACaB Bc → acB CB → DB aD → Db