algoritmy fdtd a FDM pro analýzu MHOF
optické světlo je elektromagnetická vlna v přírodě, a tak jeho šíření vlastnosti se řídí zákony elektrodynamiky, které jsou souhrnně známé jako Maxwellovy rovnice. Je známo, že vedení světelných signálů v MHOF s fotonickými strukturami pásma závisí na konstruktivním interferenčním efektu v důsledku periodického uspořádání identických vzduchových otvorů. Na druhé straně, když se vzduchové otvory stanou náhodnými ve velikosti, umístění nebo obojí, dochází k jevu úplného vnitřního odrazu a indexový rozdíl mezi jádrem a obkladem poskytuje omezení světla a tím i vedení světla podél vlákna. Ačkoli charakteristiky šíření komplikovaných struktur, jako jsou libovolné MHOFs, nelze snadno vypočítat pomocí analytických metod, existují způsoby, jak numericky řešit elektromagnetické problémy.
v této části jsou řešeny dvě numerické techniky časové domény konečných rozdílů (FDTD) a metody konečných rozdílů (FDM) s ohledem na rozšíření analýzy děrovaných optických vláken s libovolnými distribucemi vzduchových děr. Každá z těchto technik má určité výhody. Pomocí metody FDTD se kontinuální elektromagnetické pole v konečném objemu prostoru vzorkuje v různých bodech v vesmírné mřížce a ve stejně vzdálených bodech odběru vzorků v čase. Vzorkovaná data v bodech se používají pro numerické výpočty povolených režimů, aniž by se v daném vlnovodu generovala řešení rušivých režimů. Přestože je metoda FDTD efektivní technikou pro výpočet množení konstant řízených režimů, není vhodná pro vyhodnocení rozdělení jednotlivých polí režimu. Je to proto, že zdrojem je impulsní funkce v časové oblasti pokrývající nekonečné spektrum, takže řešení distribuce pole jsou superpozicí všech možných režimů. Pro zmírnění tohoto problému pomocí propagačních konstant dostupných z FDTD jsou jednotlivé distribuce polí režimu získávány pomocí FDM, které mohou rychle a pohodlně poskytovat řešení jednotlivých polí režimu.
Fdtd získal v posledních letech značnou popularitu, protože tato metoda poskytuje robustní řešení založená na Maxwellových rovnicích a může snadno pojmout komplexní vlastnosti materiálu. Libovolný objekt materiálu může být aproximován vytvořením jednotkových buněk, pro které jsou uspořádány polohy složek pole s požadovanými hodnotami permitivity a permeability. Jakmile je geometrie objektu zadána v oblasti numerické simulace, je podmínka zdroje modelována někde v oblasti. Zpočátku se předpokládá, že všechna pole v doméně výpočtu jsou shodně nulová. Poté je vynucena incidentová vlna pro vstup do oblasti numerického výpočtu.
pomocí systému jednotek MKS uvažujme nejprve Maxwellovy curlovy rovnice vyjádřené jako:
kde ε je konstanta elektrické permitivity V F / m a μ je konstanta magnetické permeability v H / m. rozšiřováním zvlněných výrazů a vyrovnáváním podobných složek se vytvoří systém šesti vázaných parciálních diferenciálních rovnic pro FDTD analýzu interakcí elektromagnetických vln s obecnými trojrozměrnými objekty. Je třeba poznamenat, že složky elektrického a magnetického pole (Ex, Ey, Ez, Hx, Hy a Hz) jsou vzájemně propojeny. To znamená, že Maxwellovy rovnice nepřinášejí přímo hodnoty elektrického a magnetického pole, ale spíše se týkají rychlosti změny mezi hodnotami elektrického a magnetického pole.
přijetím centrální aproximace konečných rozdílů pro prostorové a časové derivace s přesností na druhý řád lze vyvinout následující aproximace jako reprezentativní příklady v trojrozměrné (3D) formulaci FDTD:
kde I, J, k a n jsou celá čísla pro δx, δy, δz a δt jako přírůstky prostoru a času .
protože optická vlákna, jako jsou MHOFs, obecně nemají žádné odchylky ve směru šíření a variace materiálových vlastností jsou omezeny na příčné směry, jak je znázorněno na obrázku 3, může být formulace 3D FDTD zjednodušena na kompaktní dvourozměrný (2D) fdtd algoritmus . Použitím fázorové notace s konstantou axiálního šíření (β) jsou parciální derivace prvního řádu vzhledem k z nahrazeny-jß, protože z-závislost polí je jako exp (- jßz). A dvě sousední pole potřebná pro derivace prvního řádu v diskretizované oblasti prostoru mohou být reprezentována polem ve středu mezi nimi. Na základě těchto dvou skutečností se získá následující formulace jako příklad:
výsledný 2D algoritmus využívá významného snížení požadované alokace paměti počítače a doby běhu. Pro počítačový výpočet libovolných vlnovodů, které jsou rovnoměrné ve směru šíření vln, tedy postačuje pouze modelování průřezů vlnovodů.
spolu s tímto efektivním algoritmem je třeba pečlivě modelovat nekonečná média ve 2D prostoru pro libovolný elektromagnetický objekt, protože paměť počítače je ve výpočtové oblasti omezena i při pokročilé současné technologii. Aby bylo možné modelovat oblasti sahající do nekonečna, je na vnější hranici mřížky výpočetní domény navržena dokonale sladěná vrstva (PML) jako vysoce účinná absorpční hraniční podmínka (ABC). V ideálním případě je absorpční médium pouze tak silné jako několik mřížkových buněk, vysoce absorbující, Bez odrazu na všechny nárazové vlny a účinné v celém rozsahu provozních vlnových délek.
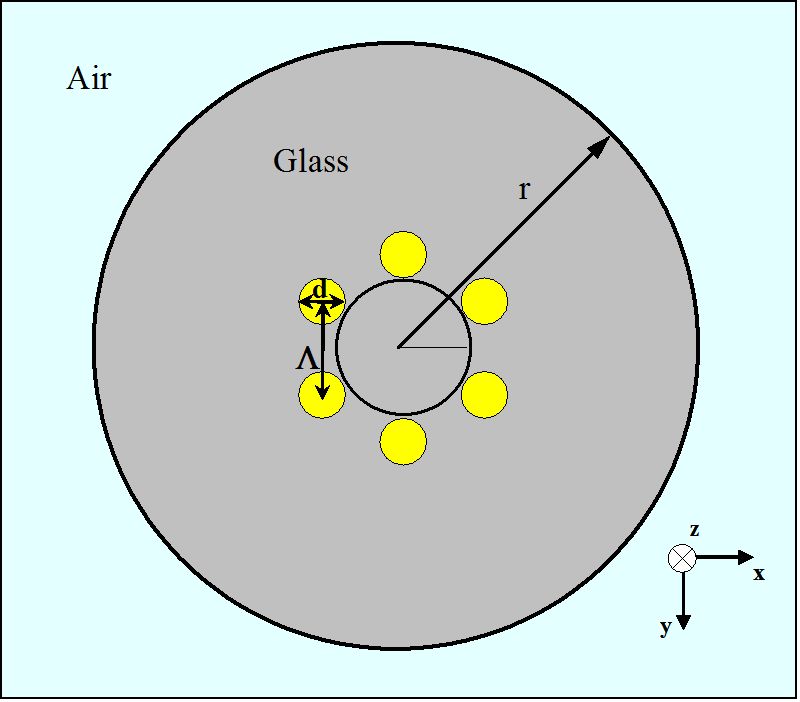
obrázek 3.
schéma průřezu MHOF s jednou vrstvou vzduchových otvorů v šestihranném uspořádání
podobně jako vývoj algoritmu FDTD lze formulaci FDM odvodit z vázaných Maxwellových rovnic . Pro spojité vlny v lineárních a izotropních médiích má kombinace Eqs (2) a (3) za následek následující rovnici vektorových vln:
kde n je index lomu a k0 je množící konstanta ve volném prostoru. Mnoho vlnovodných zařízení, jako jsou optická vlákna, lze považovat za z-invariantní nebo po částech z-invariantní struktury. U těchto struktur se index lomu n(x, y,z) mění pomalu ve směru šíření z, což platí pro většinu fotonických zařízení s vedenými vlnami. Pomocí vektorové identity∇×∇×=∇(∇⋅)−∇2, Eq (8)lze zapsat jako
také s rozumným předpokladem zanedbatelné časové závislosti podél osy Z lze formulaci FDM jako v Eq (9) implementovat nahrazením prostorových derivací konečnými diferenčními aproximacemi. Zde je třeba uvést, že příčné složky (9) je
kde index „t“ je zkratka pro příčné složky. Vzhledem k tomu, že podélná složka může být snadno získána použitím následujícího omezení nulové divergence (Gaussův zákon) :
příčné složky jsou dostatečné k popisu plně vektorových povah elektromagnetického pole v optickém vlnovodu.
pro počáteční zkoumání naváděcích vlastností MHOFs je optické vlákno znázorněné na obrázku 3 počítačově analyzováno. Obecně lze geometrii MHOF popsat dvěma parametry, délkou rozteče (Λ) a průměrem (d), jak je znázorněno na obrázku 3. Zde je délka rozteče vzdálenost mezi středy dvou nejbližších vzduchových otvorů s válcovým tvarem. Pro MHOF na obrázku 3 má každý malý vzduchový otvor průměr 1,4 µm, tvořící šestiúhelník s Λ = 1,7 µm. Skleněná část obklopující šest vzduchových otvorů žlutých oblastí má index lomu 1,45. Předpokládá se, že vnější poloměr (r) děrovaného vlákna je 10 µm. Také vnější oblast MHOF je vzduch.
jakmile je průřez děrovaného vlákna definován ve správné výpočetní doméně, může být simulace FDTD provedena s několika specifikovanými parametry, jako je τ při definování Gaussova zdroje, Δt pro stabilní simulaci, celkový počet (ntot) časových kroků pro vzorkování dat v časové oblasti a přiměřené hodnoty β. Zde, aby se zabránilo numerické divergenci a zajistila stabilita algoritmu FDTD, musí být vybrána vhodná Δt, aby splnila následující podmínku stability:
kde cM je maximální rychlost vlnové fáze v daném numerickém modelu. Shrnutí mechanismu za analýzou FDTD, počítačová simulace probíhá následujícími kroky:
-
zvolte vhodné hodnoty parametrů (τ, Δt, ntot a β)
-
vzorkování dat komponenty pole v časové doméně
-
vezměte Fourierovu transformaci časových dat
-
získejte spektrální data složky pole
-
zvolte frekvence režimu spojené s hodnotou β
-
Sbírejte údaje o β a frekvenci režimu
-
vytvořte graf indexu režimu versus vlnová délka
obrázek 4 znázorňuje charakteristické křivky, které jsou získány z fdtd výpočet pro první tři režimy nižšího řádu MHOF definované na obrázku 3.
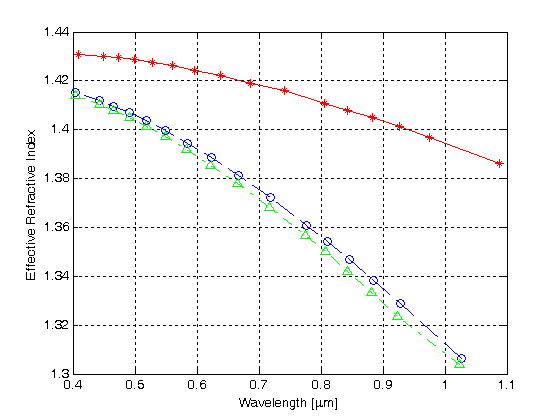
obrázek 4.
efektivní index lomu versus vlnová délka pro první tři režimy v MHOF s jednou vrstvou vzduchových otvorů
červená křivka se symboly hvězd vykresluje normalizovanou konstantu šíření pro první režim versus vlnovou délku, zatímco modré a zelené křivky ukazují normalizované konstanty šíření pro druhý a třetí režim. Výsledky ukazují, že hmof s jednou šestihrannou vrstvou Opláštění vzduchovým otvorem podporuje multimodové vedení.