klusteranalys

Posted on by admin

bedömning | Biopsykologi | jämförande |kognitiv | utvecklings | språk | individuella skillnader |personlighet | filosofi | Social |
metoder | statistik |klinisk | pedagogisk | industriell |professionell objekt |världspsykologi |

statistik:vetenskaplig metod · forskningsmetoder · experimentell design · grundutbildning statistik kurser · statistiska tester · spelteori · beslutsteori

denna artikel behöver omskrivning för att förbättra dess relevans för psykologer..
hjälp till att förbättra den här sidan själv om du kan..

klusteranalys eller kluster är en vanlig teknik för statistisk dataanalys, som används inom många områden, inklusive maskininlärning, datautvinning, mönsterigenkänning, bildanalys och bioinformatik. Clustering är klassificeringen av liknande objekt i olika grupper, eller mer exakt, uppdelningen av en datamängd i delmängder (kluster), så att data i varje delmängd (helst) delar något gemensamt drag – ofta närhet enligt något definierat avståndsmått.

förutom termen data clustering (eller bara clustering) finns det ett antal termer med liknande betydelser, inklusive klusteranalys, automatisk klassificering, numerisk taxonomi, botryologi och typologisk analys.

typer av kluster

dataklusteringsalgoritmer kan vara hierarkiska eller partitionella. Hierarkiska algoritmer hittar successiva kluster med hjälp av tidigare etablerade kluster, medan partitionella algoritmer bestämmer alla kluster samtidigt. Hierarkiska algoritmer kan vara agglomerativa (bottom-up) eller splittrande (top-down). Agglomerativa algoritmer börjar med varje element som ett separat kluster och sammanfogar dem i successivt större kluster. Delande algoritmer börjar med hela uppsättningen och fortsätter att dela upp den i successivt mindre kluster.

hierarkisk clustering

avståndsmått

ett viktigt steg i en hierarkisk clustering är att välja ett avståndsmått. Ett enkelt mått är manhattan avstånd, lika med summan av absoluta avstånd för varje variabel. Namnet kommer från det faktum att variablerna i ett tvåvariabelfall kan ritas på ett rutnät som kan jämföras med stadsgator, och avståndet mellan två punkter är antalet block som en person skulle gå.

ett vanligare mått är euklidiskt avstånd, beräknat genom att hitta kvadraten på avståndet mellan varje variabel, summera rutorna och hitta kvadratroten av den summan. I det tvåvariabla fallet är avståndet analogt med att hitta hypotenusens längd i en triangel; det vill säga det är avståndet ”som kråken flyger.”En genomgång av klusteranalys i hälsopsykologisk forskning fann att det vanligaste avståndsmåttet i publicerade studier inom det forskningsområdet är det euklidiska avståndet eller det kvadrerade euklidiska avståndet.

skapa kluster

givet ett avståndsmått kan element kombineras. Hierarkisk kluster bygger (agglomerativ) eller bryter upp (splittrande), en hierarki av kluster. Den traditionella representationen av denna hierarki är en träddatastruktur (kallad ett dendrogram), med enskilda element i ena änden och ett enda kluster med varje element i den andra. Agglomerativa algoritmer börjar längst upp i trädet, medan splittrande algoritmer börjar längst ner. (I figuren indikerar pilarna en agglomerativ kluster.)

att klippa trädet i en given höjd ger en kluster med en vald precision. I följande exempel kommer skärning efter den andra raden att ge kluster {a} {b c} {d e} {f}. Skärning efter den tredje raden ger kluster {a} {b c} {d e f}, vilket är en grovare kluster, med färre antal större kluster.

Agglomerativ hierarkisk gruppering

Antag till exempel att dessa data ska grupperas. Där euklidiskt avstånd är avståndsmätvärdet.

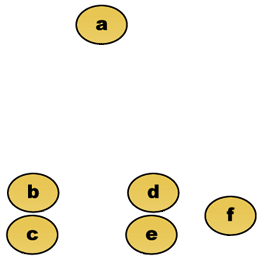
rådata

den hierarkiska klustring dendrogram skulle vara som sådan:

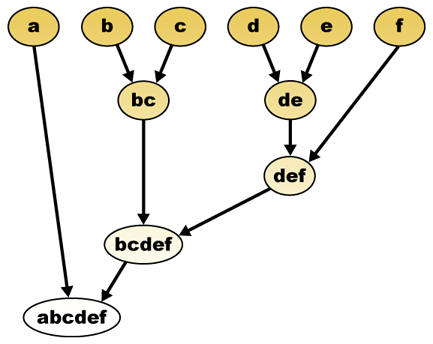
traditionell representation

denna metod bygger hierarkin från de enskilda elementen genom att gradvis slå samman kluster. Återigen har vi sex element {A} {b} {c} {d} {e} och {f}. Det första steget är att bestämma vilka element som ska slås samman i ett kluster. Vanligtvis vill vi ta de två närmaste elementen, därför måste vi definiera ett avstånd {\displaystyle d (\mathrm {element} _ {1},\mathrm {element} _{2})} mellan elementen. Man kan också konstruera en avståndsmatris i detta skede.

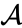
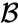
Antag att vi har slagit samman de två närmaste elementen b och c, Vi har nu följande kluster {a}, {b, c}, {d}, {e} och {f} och vill slå samman dem ytterligare. Men för att göra det måste vi ta avståndet mellan {A} och {b c} och därför definiera avståndet mellan två kluster. Vanligtvis är avståndet mellan två kluster {\displaystyle {\mathcal {A}}} och {\displaystyle {\mathcal {b}}} ett av följande:

  • det maximala avståndet mellan elementen i varje kluster (även kallad komplett koppling clustering):

{\displaystyle \ max \ { \ , d (x,y): x \ in {\mathcal {A}},\, y \ in {\mathcal {B}}\,\}}

  • det minsta avståndet mellan elementen i varje kluster (även kallad enda koppling clustering):

{\displaystyle \ min \ { \ , d (x, y):x \ in {\mathcal {A}},\, y \ in {\mathcal {B}}\,\}}

  • det genomsnittliga avståndet mellan elementen i varje kluster (även kallad Genomsnittlig länkklustring):

{\displaystyle {1 \ over {\mathrm {card} ({\mathcal {A}})\mathrm {card} ({\mathcal {B}})}}\sum _{x\in {\mathcal {A}}}\sum _{y\in {\mathcal {B}}}d (x, y)}

  • summan av all intra-cluster varians
  • ökningen av variansen för klustret som slås samman (Wards kriterium)
  • sannolikheten för att kandidatkluster Leker från samma distributionsfunktion (V-koppling)

varje agglomeration sker på ett större avstånd mellan kluster än den tidigare agglomerationen, och man kan bestämma sig för att sluta klustera antingen när klusterna är för långt ifrån varandra för att slås samman (avståndskriterium) eller när det finns ett tillräckligt litet antal kluster (talkriterium).

Partitional clustering

k-medel och derivat

K-betyder clustering

k-means-algoritmen tilldelar varje punkt till klustret vars centrum (även kallad centroid) är närmast. Centret är genomsnittet av alla punkter i klustret — det vill säga dess koordinater är det aritmetiska medelvärdet för varje dimension separat över alla punkter i klustret.

exempel: Datamängden har tre dimensioner och klustret har två punkter: X = (x1, x2, x3) och Y = (y1, y2, y3). Då blir centroid Z Z = (z1, z2, z3), där z1 = (x1 + y1)/2 och z2 = (x2 + y2)/2 och z3 = (x3 + y3)/2.

algoritmen är ungefär (J. MacQueen, 1967):

  • generera slumpmässigt k-kluster och bestäm klustercentra, eller generera direkt k-fröpunkter som klustercentra.
  • tilldela varje punkt till närmaste klustercenter.
  • beräkna om de nya klustercentren.
  • upprepa tills något konvergenskriterium är uppfyllt (vanligtvis att tilldelningen inte har ändrats).

de viktigaste fördelarna med denna algoritm är dess enkelhet och hastighet som gör det möjligt att köra på stora datamängder. Dess nackdel är att det inte ger samma resultat med varje körning, eftersom de resulterande klusterna beror på de initiala slumpmässiga uppdragen. Det maximerar inter-cluster (eller minimerar intra-cluster) varians, men säkerställer inte att resultatet har ett globalt minimum av varians.

Qt Clust algoritm

Qt (quality Threshold) Clustering (Heyer et al, 1999) är en alternativ metod för partitionering av data, uppfunnad för genklustering. Det kräver mer datorkraft än k-medel, men kräver inte att ange antalet kluster a priori, och returnerar alltid samma resultat när det körs flera gånger.

algoritmen är:

  • användaren väljer en maximal diameter för kluster.
  • Bygg ett kandidatkluster för varje punkt genom att inkludera närmaste punkt, nästa närmaste och så vidare tills klustrets diameter överstiger tröskeln.
  • spara kandidatklustret med flest poäng som det första riktiga klustret och ta bort alla poäng i klustret från ytterligare överväganden.
  • Recurse med den reducerade uppsättningen punkter.

avståndet mellan en punkt och en grupp punkter beräknas med fullständig koppling, dvs. som det maximala avståndet från punkten till någon medlem i gruppen (se avsnittet ”Agglomerativ hierarkisk kluster” om avståndet mellan kluster).

Fuzzy c-betyder kluster

i fuzzy clustering har varje punkt en grad av tillhörighet till kluster, som i fuzzy logic, snarare än att helt tillhöra bara ett kluster. Således kan punkter på kanten av ett kluster vara i klustret i mindre grad än punkter i mitten av klustret. För varje punkt x har vi en koefficient som ger graden av att vara i KTH-klustret {\displaystyle u_{k} (x)}. Vanligtvis definieras summan av dessa koefficienter som 1, så att {\displaystyle u_{k}(x)} betecknar en sannolikhet att tillhöra ett visst kluster:

{\displaystyle \forall x\sum _{k=1}^{\mathrm {num.} \ \ mathrm {kluster} }u_{k} (x)\ =1.}

med fuzzy c-medel är Centroid för ett kluster medelvärdet av alla punkter, viktade efter deras grad av tillhörighet till klustret:

{\displaystyle \mathrm {center} _{k}={{\sum _{x}u_{k}(x)x} \over {\sum _{x}u_{k}(x)}}.}

graden av tillhörighet är relaterad till det inversa avståndet till klustret

{\displaystyle u_{k} (x) = {1 \ over d(\mathrm {center} _ {k},x)},}

sedan normaliseras koefficienterna och fuzzyfieras med en verklig parameter {\displaystyle m1} så att deras summa är 1. Så

{\displaystyle u_{k} (x)={\frac {1}{\sum _{j}\vänster({\frac {d(\mathrm {center} _{k},x)} {d(\mathrm {center} _{j},x)}}\höger)^{1/(m-1)}}}.}

för m lika med 2, motsvarar detta att normalisera koefficienten linjärt för att göra summan 1. När m är nära 1, ges klustercentret närmast punkten mycket mer vikt än de andra, och algoritmen liknar k-medel.

den fuzzy C-means-algoritmen är mycket lik k-means-algoritmen:

  • Välj ett antal kluster.
  • tilldela slumpmässigt till varje punktkoefficienter för att vara i klusterna.
  • upprepa tills algoritmen har konvergerat (det vill säga koefficienternas förändring mellan två iterationer är inte mer än {\displaystyle \ epsilon }, den givna känslighetströskeln) :
    • beräkna centroid för varje kluster med hjälp av formeln ovan.
    • för varje punkt, beräkna dess koefficienter för att vara i klusterna med hjälp av formeln ovan.

algoritmen minimerar också intra-cluster-variansen, men har samma problem som k-medel, minimumet är ett lokalt minimum och resultaten beror på det ursprungliga valet av vikter.

Armbågskriterium

armbågskriteriet är en vanlig tumregel för att bestämma vilket antal kluster som ska väljas, till exempel för k-medel och agglomerativ hierarkisk kluster.

armbågskriteriet säger att du bör välja ett antal kluster så att lägga till ett annat kluster inte lägger till tillräcklig information. Mer exakt, om du graferar andelen varians som förklaras av klusterna mot antalet kluster, kommer de första klusterna att lägga till mycket information (förklara mycket varians), men vid någon tidpunkt kommer marginalförstärkningen att sjunka, vilket ger en vinkel i grafen (armbågen).

i följande diagram indikeras armbågen med den röda cirkeln. Antalet valda kluster bör därför vara 4.

förklarad varians

Spektralklustring

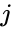
givet en uppsättning datapunkter kan likhetsmatrisen definieras som en matris {\displaystyle s} där {\displaystyle s_{ij}} representerar ett mått på likheten mellan punkt {\displaystyle i} och {\displaystyle J}. Spektrala klustringstekniker använder spektrumet av likhetsmatrisen för data för att klustera punkterna. Ibland används sådana tekniker också för att utföra dimensioneringsreduktion för kluster i färre dimensioner.

en sådan teknik är shi-Malik-algoritmen, som vanligtvis används för bildsegmentering. Den delar upp punkter i två uppsättningar {\displaystyle (S_{1}, s_{2})} baserat på egenvektorn {\displaystyle v} motsvarande Laplacians näst minsta egenvärde

{\displaystyle L=I-d^{1/2}SD^{1/2}}

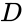
av {\displaystyle s}, där {\displaystyle D} är diagonalmatrisen

{\displaystyle D_{ii}=\sum _{j}S_{ij}.}

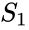
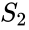
denna partitionering kan göras på olika sätt, till exempel genom att ta medianen {\displaystyle M} av komponenterna i {\displaystyle v} och placera alla punkter vars komponent i {\displaystyle v} är större än {\displaystyle M} i {\displaystyle s_{1}} och resten i {\displaystyle s_{2}}. Algoritmen kan användas för hierarkisk gruppering genom att upprepade gånger partitionera delmängderna på detta sätt.

en relaterad algoritm är meila-Shi-algoritmen, som tar egenvektorerna som motsvarar de k största egenvärdena i matrisen {\displaystyle P=SD^{-1}} för vissa k, och åberopar sedan en annan (t.ex. k-medel) till klusterpunkter med sina respektive k-komponenter i dessa egenvektorer.

tillämpningar

biologi

i biologi clustering har många tillämpningar inom områdena beräkningsbiologi och bioinformatik, varav två är:

  • i transkriptomik används kluster för att bygga grupper av gener med relaterade uttrycksmönster. Ofta innehåller sådana grupper funktionellt relaterade proteiner, såsom enzymer för en specifik väg, eller gener som är samreglerade. Experiment med hög genomströmning med uttryckta sekvenstaggar (ESTs) eller DNA-mikroarrayer kan vara ett kraftfullt verktyg för genomanteckning, en allmän aspekt av genomik.
  • i sekvensanalys används kluster för att gruppera homologa sekvenser i genfamiljer. Detta är ett mycket viktigt begrepp inom bioinformatik och evolutionär biologi i allmänhet. Se evolution genom genduplikation.

marknadsundersökning

klusteranalys används ofta i marknadsundersökningar när man arbetar med multivariata data från undersökningar och testpaneler. Marknadsundersökare använder klusteranalys för att dela upp konsumenternas allmänna befolkning i marknadssegment och för att bättre förstå relationerna mellan olika grupper av konsumenter/potentiella kunder.

  • segmentera marknaden och bestämma målmarknader
  • produktpositionering
  • ny produktutveckling
  • välja testmarknader (se : experimentella tekniker)

andra applikationer

social nätverksanalys: i studien av sociala nätverk kan kluster användas för att känna igen samhällen inom stora grupper av människor.

Bildsegmentering: kluster kan användas för att dela upp en digital bild i olika regioner för gränsdetektering eller objektigenkänning.

data mining: många Data mining-applikationer involverar uppdelning av dataobjekt i relaterade delmängder; marknadsföringsapplikationerna som diskuterats ovan representerar några exempel. En annan vanlig applikation är uppdelningen av dokument, till exempel World Wide Web pages, i genrer.

jämförelser mellan datakluster

det har funnits flera förslag på ett mått på likhet mellan två kluster. En sådan åtgärd kan användas för att jämföra hur väl olika dataklusteringsalgoritmer fungerar på en uppsättning data. Många av dessa åtgärder härrör från matchningsmatrisen (aka förvirringsmatris), t.ex. Rand-måttet och Fowlkes-Mallows Bk-måtten.

  • Jain, Murty och Flynn: data Clustering: en översyn, ACM Comp. Surv., 1999. Finns här.
  • för en annan presentation av hierarkiska, k-medel och fuzzy c-medel se denna introduktion till kluster. Har också en förklaring på blandning av Gaussier.
  • David Dowe, blandning modellering sida-andra kluster och blandning modell länkar.
  • en handledning om kluster
  • online-läroboken: informationsteori, inferens och inlärningsalgoritmer, av David Jc MacKay innehåller kapitel om k-means clustering, soft k-means clustering och derivat inklusive E-m-algoritmen och variationsvyn för E-m-algoritmen.

Se även

  • k-betyder
  • artificiellt neuralt nätverk (ANN)
  • självorganiserande karta
  • Förväntningsmaximering (EM)

bibliografi

  • Clatworthy, J., Buick, D., Hankins, M., Weinman, J., & Horne, R. (2005). Användning och rapportering av klusteranalys i hälsopsykologi: en översyn. British Journal of Health Psychology 10: 329-358.
  • Romesburg, H. Clarles, klusteranalys för forskare, 2004, 340 s. ISBN 1411606175 eller utgivare, omtryck av 1990-upplagan publicerad av Krieger Pub. Co… En japansk språköversättning är tillgänglig från Uchida Rokakuho Publishing Co., Ltd., Tokyo, Japan.
  • Heyer, lj, Kruglyak, S. och Yooseph, S., utforska Uttrycksdata: identifiering och analys av Samuttryckta gener, genomforskning 9:1106-1115.
  • online-läroboken: informationsteori, inferens och inlärningsalgoritmer, av David J. C. MacKay innehåller kapitel om k-means clustering, soft k-means clustering och derivat inklusive E-m-algoritmen och variationsvyn för E-m-algoritmen.

för spektralklustring :

  • Jianbo Shi och Jitendra Malik, ”normaliserade snitt och Bildsegmentering”, IEEE-transaktioner på mönsteranalys och maskinintelligens, 22(8), 888-905, augusti 2000. Tillgänglig på Jitendra Maliks hemsida
  • Marina Meila och Jianbo Shi, ”Learning Segmentation with Random Walk”, Neural Information Processing Systems, NIPS, 2001. Tillgänglig från Jianbo Shis hemsida

för uppskattning av antal kluster:

  • Can, F., Ozkarahan, E. A. (1990) ” begrepp och effektivitet i den coverkoefficientbaserade klustermetoden för textdatabaser.”ACM transaktioner på databassystem. 15 (4) 483-517.

programvaruimplementeringar

gratis

  • flexclust-paketet för R
  • YALE (ännu en inlärningsmiljö): gratis programvara med öppen källkod för kunskapsupptäckt och datautvinning, inklusive ett plugin för kluster
  • några Matlab – källfiler för kluster här
  • compact-jämförande paket för klusterbedömning (även i Matlab)
  • mixmod : Modellbaserad Kluster-Och Diskrimineringsanalys. Kod i C++, gränssnitt med Matlab och Scilab
  • LingPipe Clustering Tutorial Tutorial för att göra komplett – och single-link clustering med LingPipe, en Java text data mining paket distribueras med source.
  • Weka: Weka innehåller verktyg för dataförbehandling, klassificering, regression, kluster, associeringsregler och visualisering. Det är också väl lämpad för att utveckla nya system maskininlärning.

Lämna ett svar

Din e-postadress kommer inte publiceras.