antagen kunskap
studenter kommer att ha haft omfattande informell erfarenhet av geometri tidigare år, och detta kommer att ge en bra intuitiv grund för det mer systematiska tillvägagångssättet för geometri som är lämpligt i år 7-10. De särskilda ämnen från år F-6 som är relevanta för denna modul är:
- användning av kompasser och linjaler och noggrann ritning av geometriska figurer.
- typer av vinklar, inklusive åtminstone rätvinklar, akuta vinklar, trubbiga vinklar och
reflexvinklar. - trianglar, inklusive en informell introduktion till isosceles och liksidiga trianglar.
- Quadrilaterals, inklusive en informell introduktion till kvadrater, rektanglar, parallellogram, trapezier och rhombuses.
- informell erfarenhet av översättningar, reflektioner, rotationer och utvidgningar,
och med symmetri i samband med aktiviteter som vikning av en likbent triangel, rektangel eller romb.
Motivation
 geometri används för att modellera världen omkring oss. En vy över husets tak avslöjar trianglar, trapezier och rektanglar, medan kakelmönster i trottoarer och badrum använder hexagoner, pentagoner, trianglar och rutor.
geometri används för att modellera världen omkring oss. En vy över husets tak avslöjar trianglar, trapezier och rektanglar, medan kakelmönster i trottoarer och badrum använder hexagoner, pentagoner, trianglar och rutor.
byggare, plattsättare, arkitekter, grafiska formgivare och webbdesigners använder rutinmässigt geometriska ideer i sitt arbete. Att klassificera sådana geometriska objekt och studera deras egenskaper är mycket viktigt. Geometri har också många tillämpningar inom konst.
precis som aritmetik har siffror som sina grundläggande studieobjekt, så är punkter, linjer och cirklar de grundläggande byggstenarna i plangeometri.
i gymnasiegeometri börjar vi med ett antal intuitiva ideer (punkter, linjer och vinklar) som inte alls är lätta att exakt definiera, följt av vissa definitioner (vertikalt motsatta vinklar, parallella linjer osv.) och från dessa härleder vi viktiga fakta, som ofta kallas satser. I gymnasiet bör nivån på noggrannhet utvecklas långsamt från ett år till ett annat, men i varje steg är tydlig inställning mycket viktig och bör betonas.
således ger geometri en möjlighet för studenter att utveckla sin geometriska intuition, som har tillämpningar inom många områden i livet, och också att lära sig att konstruera logiska argument och göra avdrag i en inställning som För det mesta är oberoende
av nummer.
innehåll
punkter och linjer
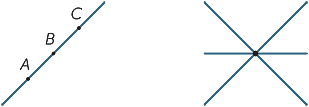
de enklaste objekten i plangeometri är punkter och linjer. Eftersom de är så enkla är det svårt att ge exakta definitioner av dem, så istället strävar vi efter att ge eleverna en grov beskrivning av deras egenskaper som ligger i linje med vår intuition. En punkt markerar en position men har ingen storlek. I praktiken, när vi ritar en punkt, har den tydligt en bestämd bredd, men den representerar en punkt i vår fantasi. En linje har ingen bredd och sträcker sig oändligt i båda riktningarna. När vi ritar en linje har den bredd och den har ändar, så det är inte riktigt en linje utan representerar en linje i vår fantasi. Med tanke på två distinkta punkter A och B finns det en (och endast en) linje som passerar genom båda punkterna. Vi använder stora bokstäver för att hänvisa till punkter och namnlinjer antingen genom att ange två punkter på linjen eller genom att använda små bokstäver som  och m. således kallas den angivna raden nedan som linjen AB eller som linjen
och m. således kallas den angivna raden nedan som linjen AB eller som linjen  .
.

med tanke på två distinkta linjer finns det två möjligheter: de kan antingen träffas vid en enda punkt eller de kan aldrig träffas, oavsett hur långt de förlängs (eller produceras). Linjer som aldrig möts kallas parallella. I det andra diagrammet skriver vi AB ||CD.
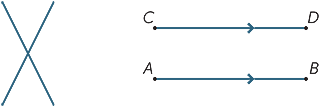
tre (eller fler) punkter som ligger på en rak linje kallas collinear.
tre (eller fler) linjer som möts vid en enda punkt kallas samtidig.
|
|
|
| Collinear |
samtidig |
Övning 1
Rita tre linjer som inte är samtidiga så att inga två är parallella.
Övning 2
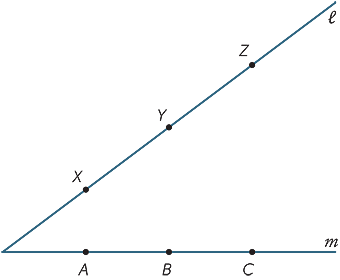
gör en stor kopia av diagrammet nedan. Punkterna X, Y, Z är några punkter på linjen  och A, B, C är några punkter på linjen m. gå med i AY och XB kallar deras korsning R. gå med i BZ och YC och ring deras korsning P. gå med i CX och ZA och ring deras korsning Q. vad märker du om punkterna P, Q, R? (Detta resultat kallas Pappus sats, c. 340 e. Kr.)
och A, B, C är några punkter på linjen m. gå med i AY och XB kallar deras korsning R. gå med i BZ och YC och ring deras korsning P. gå med i CX och ZA och ring deras korsning Q. vad märker du om punkterna P, Q, R? (Detta resultat kallas Pappus sats, c. 340 e. Kr.)
intervall, strålar och vinklar
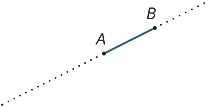 Antag att A och B är två punkter på en rad. Intervallet
Antag att A och B är två punkter på en rad. Intervallet
AB är den del av linjen mellan A och B, inklusive de två slutpunkterna.
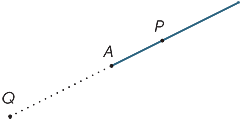 punkten A i diagrammet delar upp linjen i två delar som kallas strålar. Ray AP är den stråle som innehåller punkten P (och punkten A).
punkten A i diagrammet delar upp linjen i två delar som kallas strålar. Ray AP är den stråle som innehåller punkten P (och punkten A).
Vinklar
 i diagrammet kallas det skuggade området mellan strålarna OA och OB vinkeln AOB eller vinkeln BOA. Vinkeltecknet
i diagrammet kallas det skuggade området mellan strålarna OA och OB vinkeln AOB eller vinkeln BOA. Vinkeltecknet ![]() är skrivet så vi skriver
är skrivet så vi skriver ![]() AOB.
AOB.
 det skuggade området utanför kallas reflexvinkeln som bildas av OA och OB. För det mesta, om vi inte anger ordet reflex, hänvisar alla våra vinklar till området mellan strålarna och inte utanför dem.
det skuggade området utanför kallas reflexvinkeln som bildas av OA och OB. För det mesta, om vi inte anger ordet reflex, hänvisar alla våra vinklar till området mellan strålarna och inte utanför dem.
storleken på en vinkel
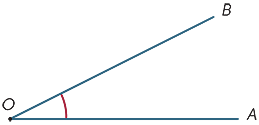 Föreställ dig att strålen OB roteras om punkten O tills den ligger längs OA. Mängden vridning kallas storleken på vinkeln AOB. Vi kan på samma sätt definiera storleken på reflexvinkeln.
Föreställ dig att strålen OB roteras om punkten O tills den ligger längs OA. Mängden vridning kallas storleken på vinkeln AOB. Vi kan på samma sätt definiera storleken på reflexvinkeln.
vi kommer ofta att använda små grekiska bokstäver, 2, xnumx, xnumx, xnumx, xnumx, xnumx … att representera storleken på en vinkel.
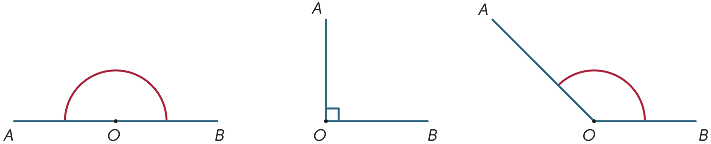
storleken på vinkeln som motsvarar en full revolution delades (av babylonierna) i 360 lika delar, som vi kallar grader. (De valde förmodligen 360 eftersom det var nära antalet dagar på ett år.) Därför är storleken på en rät vinkel 180 kg och storleken på en rät vinkel är 90 kg. Andra vinklar kan mätas (ungefär) med hjälp av en gradskiva.
|
|
||
| rät vinkel | rät vinkel |
trubbig vinkel |
vinklar klassificeras enligt deras storlek. Vi säger att en vinkel med storlek α är akuta
(ett ord som betyder ”skarp”) vid 0° < α < 90°, α är trubbig (ett ord som betyder ”trubbig”), om
90° < α < 180° och α är reflex om 180° < α < 360°.
eftersom gradskivan har två skalor måste eleverna vara försiktiga när de ritar och
mäter vinklar. Det är en värdefull övning att använda en gradskiva för att rita några vinklar som 30°, 78°, 130°, 163°.
Övning 3
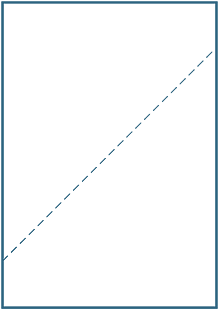 Vik ett A4-pappersark som matchar de (diagonalt) motsatta hörnen. Rita en linje längs vecket som bildas och mät vinklarna mellan vecket och sidan.
Vik ett A4-pappersark som matchar de (diagonalt) motsatta hörnen. Rita en linje längs vecket som bildas och mät vinklarna mellan vecket och sidan.
i övningen ovan bildar de två vinklarna tillsammans en rak linje och lägger så till 180 kcal. Två vinklar för att lägga till 180° kallas kompletterande vinklar, alltså 45° och 135° är kompletterande vinklar.
två vinklar som lägger till 90 kcal kallas komplementära; således är 23 kcal och 67 kcal
komplementära vinklar.
vinklar vid en punkt
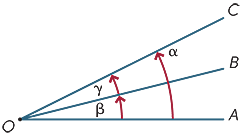 två vinklar vid en punkt sägs vara intill om de delar en gemensam stråle. I diagrammet ligger därför
två vinklar vid en punkt sägs vara intill om de delar en gemensam stråle. I diagrammet ligger därför ![]() AOB och
AOB och ![]() BOC intill varandra.
BOC intill varandra.
intilliggande vinklar kan läggas till, så i diagrammet
https: / /
när två linjer skär varandra bildas fyra vinklar vid skärningspunkten.
i diagrammet kallas vinklarna markerade ![]() AOX och
AOX och ![]() BOY vertikalt motsatta.
BOY vertikalt motsatta.
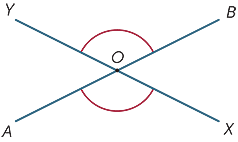 sedan
sedan
-
 AOX är tillägget av
AOX är tillägget av  BOX (rak vinkel).
BOX (rak vinkel). -
 BOY är också tillägget av
BOY är också tillägget av  BOX (rak vinkel),
BOX (rak vinkel),
vi kan dra slutsatsen att dessa vertikalt motsatta vinklar, ![]() AOX och
AOX och ![]() BOY är lika. Vi har alltså vårt första
BOY är lika. Vi har alltså vårt första
viktiga geometriska uttalande:
vertikalt motsatta vinklar är lika.
ett resultat i geometri (och i matematik i allmänhet) kallas ofta en sats. En sats är ett viktigt uttalande som kan bevisas genom logiskt avdrag. Argumentet ovan är ett bevis på satsen; ibland presenteras bevis formellt efter uttalandet av satsen.
 om två linjer skär så att alla fyra vinklarna är rätvinkliga, sägs linjerna vara vinkelräta.
om två linjer skär så att alla fyra vinklarna är rätvinkliga, sägs linjerna vara vinkelräta.
vinklar vid en punkt-Geometriska argument
följande skäl kan användas i geometriska argument:
- intilliggande vinklar kan läggas till eller subtraheras.
- vinklar i en revolution lägga till 360 kcal.
- vinklar i en rak linje Lägg till 180 kcal.
- vertikalt motsatta vinklar är lika.
tvärgående och parallella linjer
 en tvärgående är en linje som möter två andra linjer.
en tvärgående är en linje som möter två andra linjer.
motsvarande vinklar
olika vinklar bildas av tvärgående. I diagrammen nedan kallas de två markerade vinklarna motsvarande vinklar.
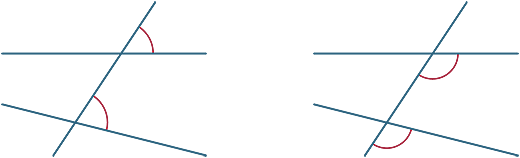
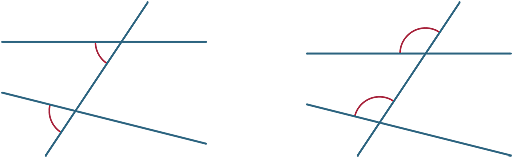
 vi tittar nu på vad som händer när de två linjerna som skärs av tvärgående är parallella.
vi tittar nu på vad som händer när de två linjerna som skärs av tvärgående är parallella.
Inituitively, om vinkeln α som var större än β sedan CD skulle korsa AB till vänster om F och om det var mindre än β, det skulle krysset till höger om F. Så eftersom linjerna inte gå på alla, α kan vara varken mindre eller mer än β och så lika med β.
alternativt kan du föreställa dig att översätta vinkeln QGD längs GF tills G sammanfaller med F. Eftersom linjerna är parallella, förväntar vi oss att vinkeln Bisexuell skulle sammanfalla med vinkeln. Denna observation leder oss till gissning att:
motsvarande vinklar bildade från parallella linjer är lika.
vi kan inte bevisa detta resultat, även om vi har visat att det är geometriskt troligt. Vi kommer att acceptera det som ett axiom av geometri. Ett axiom är ett uttalande som vi inte kan bevisa, men som är intuitivt rimligt. Observera att många av de fakta som vi redan har sagt som: intilliggande vinklar kan läggas till, och två punkter bestämmer en linje etc., är också Axiom, även om vi inte uttryckligen har angett dem på detta sätt.
alternativa vinklar
i varje diagram kallas de två markerade vinklarna alternativa vinklar (eftersom de är på alternativa sidor av tvärgående).

 om linjerna AB och CD är parallella är de alternativa vinklarna lika. Detta resultat kan nu bevisas.
om linjerna AB och CD är parallella är de alternativa vinklarna lika. Detta resultat kan nu bevisas.
![]() DGQ = cu (motsvarande vinklar, AB / / CD)
DGQ = cu (motsvarande vinklar, AB / / CD)
![]() DGQ = https: / /
DGQ = https: / /
så.
för att sammanfatta:
alternativa vinklar bildade från parallella linjer är lika.
Co-inre vinklar
slutligen, i varje diagram nedan, kallas de två markerade vinklarna co-inre vinklar och ligger på samma sida av transversalen.

om linjerna AB och CD är parallella, är det uppenbart att de inre vinklarna inte är lika men det visar sig att de är kompletterande, det vill säga deras summa är 180 kcal .
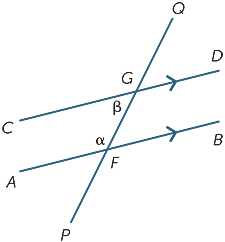 detta är ett resultat som också är lätt att bevisa:
detta är ett resultat som också är lätt att bevisa:
![]() BFG = kokos (alternativa vinklar, AB / / CD)
BFG = kokos (alternativa vinklar, AB / / CD)
kokos + kokos = 180 kokos (rak vinkel vid F)
för att sammanfatta:
Co-inre vinklar bildade från parallella linjer är kompletterande.
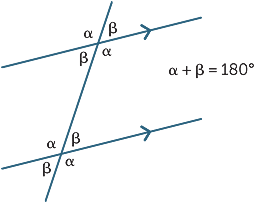 de tre resultaten kan sammanfattas
de tre resultaten kan sammanfattas
med följande diagram:
numeriska exempel
med information om vinklarna i ett diagram kan vi använda ovanstående resultat för att hitta storleken på andra vinklar i diagrammet. Detta är en enkel men mycket viktig färdighet, ofta kallad informellt som vinkeljakt. För att lösa problem är stegsekvensen inte alltid unik. Det kan finnas flera olika, men lika giltiga, tillvägagångssätt.
till exempel, i följande diagram, söker vi storleken på vinkel BAC.

![]() DCA = 102 kg (alternativa vinklar, AC|bd)
DCA = 102 kg (alternativa vinklar, AC|bd)
![]() BAC = 78 kg (Co-inre vinklar, AB / / CD)
BAC = 78 kg (Co-inre vinklar, AB / / CD)
övning 4
använd en alternativ sekvens av steg för att hitta ![]() BAC.
BAC.
Övning 5
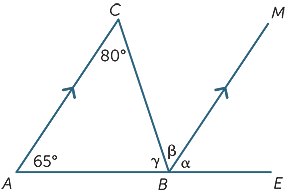 Använd endast egenskaper för parallella linjer, hitta (med skäl) de saknade vinklarna i följande diagram.
Använd endast egenskaper för parallella linjer, hitta (med skäl) de saknade vinklarna i följande diagram.
Övning 6
hitta värdet på vaniljsås i följande diagram.
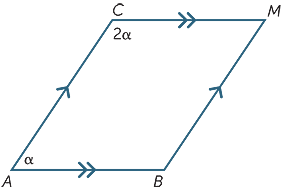
Converse uttalanden
många uttalanden i matematik har en converse, där implikationen går i motsatt riktning. Till exempel slutar uttalandet
’varje jämnt tal i 0, 2, 4, 6 eller 8.’
har converse
’ varje nummer som slutar i 0, 2, 4, 6 eller 8 är jämnt.’
detta speciella uttalande och dess omvända är båda sanna, men detta är inte alltid
fallet.
till exempel är följande två uttalanden samtal av varandra:
’varje multipel av 4 är ett jämnt tal.’
’ varje jämnt tal är en multipel av 4.’
och här är det första uttalandet sant, men det andra är falskt.
Övning 7
skriv ner:
a![]() ett sant geometriskt uttalande vars converse också är sant,
ett sant geometriskt uttalande vars converse också är sant,
b![]() falskt geometriskt uttalande vars converse är sant,
falskt geometriskt uttalande vars converse är sant,
c![]() ett falskt geometriskt uttalande vars converse också är falskt.
ett falskt geometriskt uttalande vars converse också är falskt.
Converse-satserna för parallella linjer
vi har sett att motsvarande vinklar bildade från parallella linjer är lika. Vi kan skriva ner converse-uttalandet enligt följande.
uttalande: om linjerna är parallella är motsvarande vinklar lika.
prata: Om motsvarande vinklar är lika, är linjerna parallella.
det omvända uttalandet är också sant och används ofta för att bevisa att två linjer är parallella. Detsamma gäller när det gäller alternativa och inre vinklar.
uttalande: om linjerna är parallella är de alternativa vinklarna lika.
Converse: om de alternativa vinklarna är lika, är linjerna parallella.
uttalande: om linjerna är parallella, är de inre vinklarna kompletterande.
prata: Om de inre vinklarna är kompletterande är linjerna parallella.
således är linjerna AB och CD parallella i varje diagram.

Övning 8
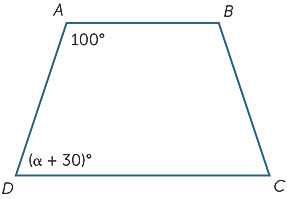 vilket värde av Macau kommer att göra AB parallellt med CD?
vilket värde av Macau kommer att göra AB parallellt med CD?
bevis på de tre samtalen
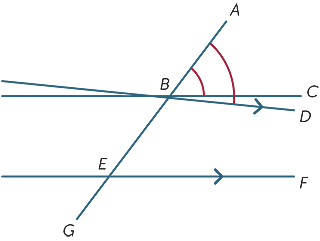 vi antar att motsvarande vinklar som bildas av tvärgående är lika och vi visar att linjerna är parallella.
vi antar att motsvarande vinklar som bildas av tvärgående är lika och vi visar att linjerna är parallella.
i diagrammet antar vi att ![]() ABC =
ABC = ![]() BEF.
BEF.
om BC och EF inte är parallella, rita sedan
BD parallellt med EF.
nu eftersom BD och EF är parallella ![]() ABD =
ABD = ![]() BEF och så
BEF och så ![]() ABC =
ABC = ![]() ABD vilket helt klart är omöjligt om inte linjerna BC och BD är desamma. Därför är linjerna BC och EF parallella.
ABD vilket helt klart är omöjligt om inte linjerna BC och BD är desamma. Därför är linjerna BC och EF parallella.
de andra bevisen följer på samma sätt.
Övning 9
ge ett bevis på den andra converse-satsen (alternativa vinklar).
vinkel summan av en triangel
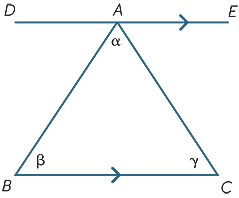 resultaten från föregående avsnitt kan användas för att härleda en av de viktigaste faktana i geometri − vinkelsumman för en triangel är 180 kcal .
resultaten från föregående avsnitt kan användas för att härleda en av de viktigaste faktana i geometri − vinkelsumman för en triangel är 180 kcal .
vi börjar med triangle ABC med vinklarna som visas. Rita linjen DAE parallellt med BC. Sedan,
![]() DAB = 6 (alternativa vinklar, BC / / DE)
DAB = 6 (alternativa vinklar, BC / / DE)
![]() EAC = (alternativ vinkel, BC||DE)
EAC = (alternativ vinkel, BC||DE)
+ + + + = 180 (rät vinkel).
Således har vi bevisat teorem
summan av vinklarna i en triangel är 180 kcal.
en fyrsidig är en planfigur avgränsad av fyra sidor.
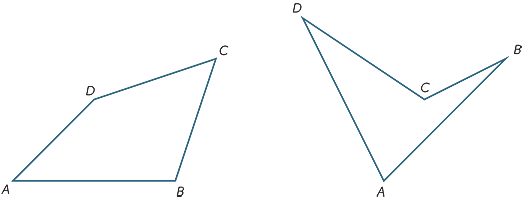
övning 10
genom att dela den fyrkantiga ABCD i två trianglar, hitta summan av vinklarna.
länkar framåt
materialet i denna modul har börjat placera geometri på en rimligt systematisk grund av noggrant definierade objekt, axiom som ska antas och satser som vi har bevisat. På grundval av detta kan vi utveckla en systematisk redogörelse för plangeometri som involverar:
- Pythagoras sats
- kongruens och kongruenta trianglar
- likhet och liknande trianglar
- isosceles och liksidiga trianglar
- speciella fyrhjulingar, inklusive kvadrater, rektanglar, parallellogram, romber och trapets
- geometrin av cirklar.
Plangeometri kommer också att vara grundläggande inom många andra områden av år 7-10 matematik:
- transformationer
- tredimensionell geometri
- områden och volymer
- trigonometri
- koordinatgeometri
- graferna i cirklar och paraboler.
tankarna om tangenter och områden leder i sin tur till kalkyl under åren 11-12.
historia och tillämpning
historia
de otroliga konstruktionerna av pyramiderna och de enorma templen i Egypten avslöjar att egyptierna måste ha haft en mycket god kunskap och förståelse för grundläggande geometri, åtminstone på praktisk nivå. Å andra sidan finns det inga bevis för att de hade systematiserat den kunskapen på något formellt sätt. Detta lämnades till de gamla grekerna. Vi har inte detaljerad kunskap om den systematiseringen, förutom påståendet att Thales (ca. 624 f. Kr. – ca. 546 f. Kr.) gav de första ’bevisen’ på geometriska fakta som markerade början på deduktiv geometri. Pythagoras skola fortsatte detta arbete och Platon (428 f.Kr. -348 f. Kr.) bygger tydligt på tidigare matematikers arbete när han nämner geometriska fakta i sina skrifter. Den geometriska dialogen i hans arbete Meno, där Sokrates får en slavpojke att komma fram till en geometrisk sats med en serie logiska avdrag, är värt att läsa. Om ursprunget till geometrin är oklart, är’ slutprodukten ’ inte. Euclid (323-283 f.Kr.), som skrev i Alexandria, producerade ett anmärkningsvärt arbete, kallat elementen, som förblev standardboken i geometri i mer än 2000 år. I detta arbete beskriver Euclid ett antal definitioner (t.ex. för punkter och linjer), postulat och vanliga begrepp. (Dessa dagar kallar vi dem axiomer.) Från dessa utvecklade han logiskt, i en mycket noggrant utvald ordning, många satser som vi i allmänhet kallar euklidisk geometri. Det finns ett antal andra geometriska resultat, såsom Pappus sats, som upptäcktes efter Euclid, men dessa täcks vanligtvis inte i gymnasiet.
en av Euclids fem postulat var inte så uppenbart sant som de andra tycktes vara. En version av den, känd som Playfairs Axiom säger att: Med tanke på en rad  och en punkt P, inte på
och en punkt P, inte på  , det finns en och endast en rad parallellt med
, det finns en och endast en rad parallellt med  passerar genom P. i den 19: e århundradet, ett antal matematiker ställde frågan ’Vad händer om vi förnekar detta postulat? Detta görs genom att anta att det antingen inte finns någon sådan parallell linje, eller genom att säga att det finns mer än en sådan linje. Detta ledde till utvecklingen av icke-euklidiska geometrier, varav en har visat sig ge en av de goda modellerna för universum.
passerar genom P. i den 19: e århundradet, ett antal matematiker ställde frågan ’Vad händer om vi förnekar detta postulat? Detta görs genom att anta att det antingen inte finns någon sådan parallell linje, eller genom att säga att det finns mer än en sådan linje. Detta ledde till utvecklingen av icke-euklidiska geometrier, varav en har visat sig ge en av de goda modellerna för universum.
tillämpningar
i en mycket verklig mening, geometri och geometrisk intuition utgör grunden för alla
matematik − geometri leder till koordinatgeometri som leder till kalkyl och
alla dess många tillämpningar − och så är avgörande i läroplanen.
på en mer praktisk nivå har byggare, lantmätare, ingenjörer och arkitekter varit tunga användare av geometri och geometriska ideer i århundraden. Mer nyligen, med utvecklingen av datorer, har grafiker och webbdesigners gått med i denna grupp människor som behöver och använder geometri i sitt arbete. På frågan nyligen hur användbar geometri är, Jim Kelly, sa en tillämpad forskare:… geometri är en viktig del av design, ritning och datormodellering. Det används också ofta i … fysik och andra fysiska vetenskapskurser som en del av att förstå effekterna av belastningar på strukturer och balanseringspunkter(tyngdpunkter) för sammansatta fasta ämnen. I kemi är förståelsen av molekylens geometri relaterad till förståelsen av ämnenas egenskaper. Många fler exempel finns. (från Ask a Scientist webbplats.)
en historia av matematik: En introduktion, 3: e upplagan, Victor J. Katz, Addison-Wesley, (2008)
matematikens historia, D. E. Smith, Dover publications New York, (1958)
svar på övningar
övning 1
ÖVNING 2
punkterna är kolinjär
TRÄNING 3
60°
TRÄNING 4
![]() DBA = 102° (motsvarande vinklar, AB| – |CD)
DBA = 102° (motsvarande vinklar, AB| – |CD)
![]() BAC = 78° (co-inre vinklarna, AC||BD -)
BAC = 78° (co-inre vinklarna, AC||BD -)
ÖVNING 5
α = 65°![]() (motsvarande vinklar, AC||BM)
(motsvarande vinklar, AC||BM)
β = 80°![]() (alternativa vinklar, AC||BM)
(alternativa vinklar, AC||BM)
γ + β = 115°![]() (co-inre vinklarna, AC||BM)
(co-inre vinklarna, AC||BM)
Därför, γ = 35°
(Det är strukturen för ett bevis av resultatet att vinkeln summan av en triangel är 180°)
Övning 6
https: / / 60
övning 7
a![]() en fyrsidig med var och en av dess inre vinklar en rät vinkel är en rektangel.
en fyrsidig med var och en av dess inre vinklar en rät vinkel är en rektangel.
Converse: varje inre vinkel i en rektangel är en rät vinkel.
b![]() en rektangel är en kvadrat
en rektangel är en kvadrat
Converse: en kvadrat är en rektangel
c![]() vinkelsumman för de inre vinklarna i en triangel är 200 kg
vinkelsumman för de inre vinklarna i en triangel är 200 kg
Converse: en polygon för vilken summan av den inre vinkeln är 200 kg är en triangel.
övning 8
https: / / 50
Övning 9
vi hänvisar till samma diagram.
placera en punkt H på linjen EF till vänster om E.
![]() CBE =
CBE = ![]() BEH
BEH
om BC och EF inte är parallella ritar du BD parallellt med EF.
eftersom BD och EF är parallella, ![]() EBD=
EBD= ![]() BEH, vilket helt klart är omöjligt om inte linjerna BC och BD är desamma.
BEH, vilket helt klart är omöjligt om inte linjerna BC och BD är desamma.
därför är linjerna BC och EF parallella.
övning 10
360°
projektet Improving Mathematics Education in Schools (TIMES) 2009-2011 finansierades av den australiensiska regeringen Department of Education, Employment and Workplace Relations.
de åsikter som uttrycks här är författarens och representerar inte nödvändigtvis synpunkterna från den australiensiska regeringen Department of Education, Employment and Workplace Relations.
Brasilien University of Melbourne på uppdrag av International Centre of Excellence för utbildning i matematik (ICE-EM), utbildningsavdelningen för Australian Mathematical Sciences Institute (AMSI), 2010 (om inte annat anges). Detta verk är licensierat enligt Creative Commons Erkännande-Ickekommersiell-IngaBearbetningar 3.0 Unported licens.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()