4.2 uppskatta koefficienterna för den linjära regressionsmodellen / introduktion till ekonometri med R

4.2 uppskatta koefficienterna för den linjära regressionsmodellen

i praktiken är intercept $\beta_0$ och lutning $\beta_1$ för populationsregressionslinjen okända. Därför måste vi använda data för att uppskatta båda okända parametrarna. I det följande kommer ett verkligt världsexempel att användas för att visa hur detta uppnås. Vi vill relatera testresultat till Student-lärarförhållanden uppmätta i kaliforniska skolor. Testresultatet är det distriktsomfattande genomsnittet av läs-och matematikpoäng för femte klassare. Återigen mäts klassstorleken som antalet elever dividerat med antalet Lärare (student-lärarförhållandet). När det gäller uppgifterna kommer California School data set (CASchools) med ett r-paket som heter AER, en akronym för Applied Econometrics with R (Kleiber and Zeileis 2020). Efter installationen av paketet med install.paket (”AER”) och bifoga det med bibliotek (AER) datamängden kan laddas med funktionen data ().

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

när ett paket har installerats är det tillgängligt för användning vid ytterligare tillfällen när det anropas med library() — det finns inget behov av att köra installationen.paket () igen!

det är intressant att veta vilken typ av objekt vi har att göra med.klass () returnerar klassen för ett objekt. Beroende på klassen av ett objekt Vissa funktioner (till exempel plot() och sammanfattning()) beter sig annorlunda.

Låt oss kontrollera klassen av objektet CASchools.

class(CASchools)#> "data.frame"

det visar sig att CASchools är av klassdata.ram som är ett bekvämt format att arbeta med, särskilt för att utföra regressionsanalys.

med hjälp av head() får vi en första översikt över våra data. Den här funktionen visar endast de första 6 raderna i datamängden som förhindrar en överfull konsolutgång.

tryck på ctrl + L för att rensa konsolen. Detta kommando tar bort all kod som har skrivits in och exekverats av dig eller skrivits ut till konsolen av R-funktioner. Den goda nyheten är att allt annat lämnas orört. Du förlorar varken definierade variabler etc. inte heller kodhistoriken. Det är fortfarande möjligt att återkalla tidigare utförda r-kommandon med upp-och nedknapparna. Om du arbetar i RStudio trycker du på ctrl + upp på tangentbordet (CMD + upp på en Mac) för att granska en lista med tidigare inmatade kommandon.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

vi finner att datamängden består av många variabler och att de flesta är numeriska.

förresten: ett alternativ till klass() och huvud() är str() som härleds från ’struktur’ och ger en omfattande översikt över objektet. Försök!

återgå till CASchools, de två variablerna vi är intresserade av (dvs., genomsnittligt testresultat och förhållandet mellan elev och lärare) ingår inte. Det är emellertid möjligt att beräkna både från de angivna uppgifterna. För att få student-lärarförhållandena delar vi helt enkelt antalet elever med antalet lärare. Den genomsnittliga testpoängen är det aritmetiska medelvärdet av testpoängen för läsning och poängen för matteprovet. Nästa kodbit visar hur de två variablerna kan konstrueras som vektorer och hur de läggs till CASchools.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

om vi sprang huvudet (CASchools) igen skulle vi hitta de två variablerna av intresse som ytterligare kolumner som heter STR och score (kolla här!).

tabell 4.1 från läroboken sammanfattar fördelningen av testresultat och student-lärarförhållanden. Det finns flera funktioner som kan användas för att ge liknande resultat, t. ex.,

medelvärde () (beräknar det aritmetiska medelvärdet av de angivna siffrorna),
sd () (beräknar provets standardavvikelse),
quantile () (returnerar en vektor av de angivna provkvantilerna för data).

nästa kodbit visar hur man uppnår detta. Först beräknar vi sammanfattande statistik på kolumnerna STR och poäng för CASchools. För att få bra resultat samlar vi in åtgärderna i en data.ram som heter DistributionSummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

när det gäller provdata använder vi plot(). Detta gör det möjligt för oss att upptäcka egenskaper hos våra data, till exempel avvikare som är svårare att upptäcka genom att titta på bara siffror. Den här gången lägger vi till några ytterligare argument till Call of plot().

det första argumentet i vår call of plot(), score ~ STR, är återigen en formel som anger variabler på y – och x-axeln. Men den här gången sparas inte de två variablerna i separata vektorer utan är kolumner av CASchools. Därför skulle R inte hitta dem utan att argumentdata anges korrekt. uppgifterna måste överensstämma med namnet på uppgifterna.ram som variablerna tillhör, i detta fall CASchools. Ytterligare argument används för att ändra plottets utseende: medan main lägger till en titel lägger xlab och ylab till anpassade etiketter på båda axlarna.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")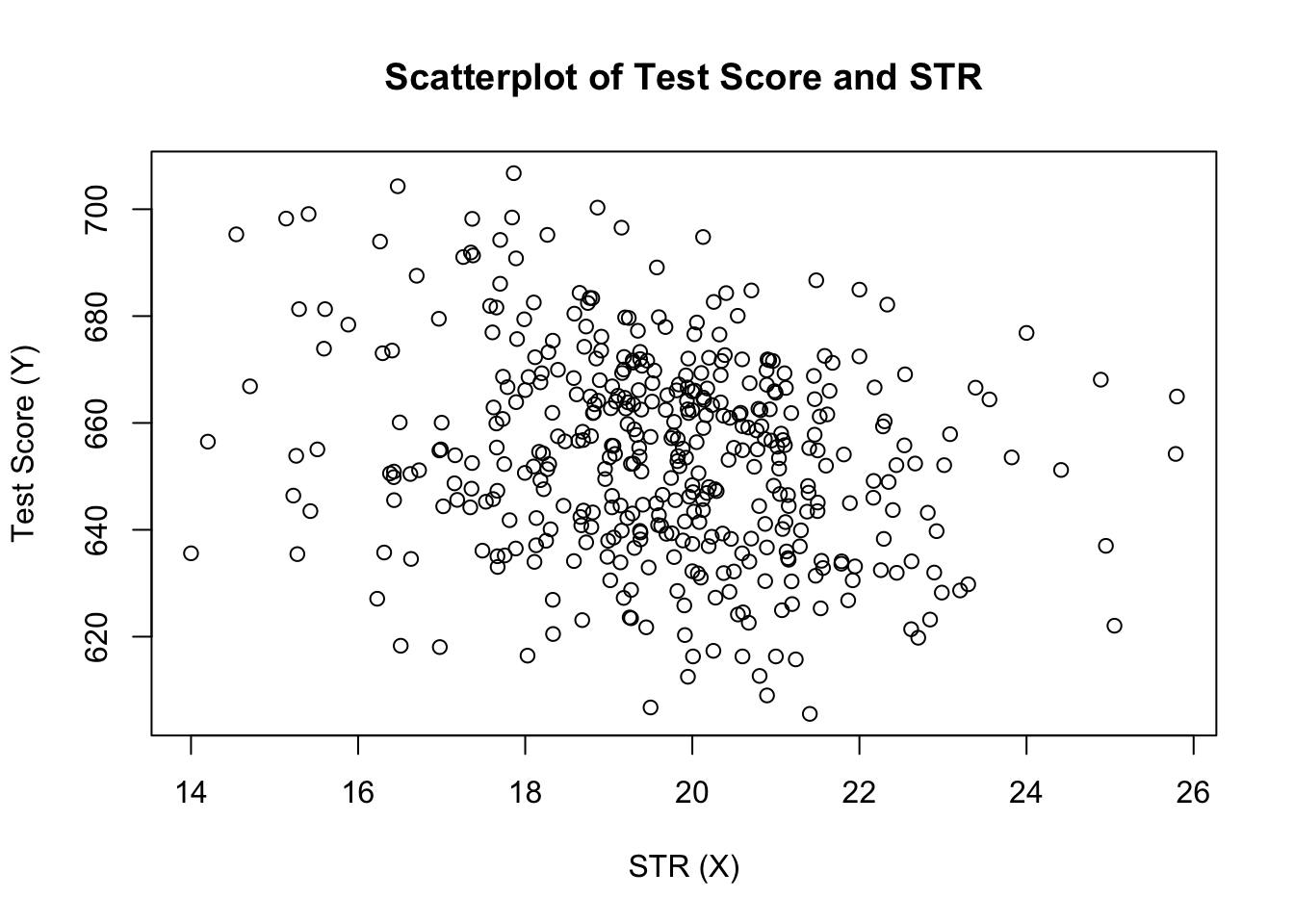

handlingen (figur 4.2 i boken) visar spridningen av alla observationer om förhållandet mellan elev och lärare och testresultat. Vi ser att punkterna är starkt utspridda och att variablerna är negativt korrelerade. Det vill säga vi förväntar oss att observera lägre testresultat i större klasser.

funktionen cor () (se ?cor för ytterligare information) kan användas för att beräkna korrelationen mellan två numeriska vektorer.

cor(CASchools$STR, CASchools$score)#> -0.2263627

som scatterplot redan antyder är korrelationen negativ men ganska svag.

uppgiften vi nu står inför är att hitta en linje som bäst passar data. Naturligtvis kunde vi helt enkelt hålla fast vid grafisk inspektion och korrelationsanalys och sedan välja den bästa passande linjen genom att eyeballing. Detta skulle dock vara ganska subjektivt: olika observatörer skulle dra olika regressionslinjer. På detta konto är vi intresserade av tekniker som är mindre godtyckliga. En sådan teknik ges genom vanlig minsta kvadrat (OLS) uppskattning.

den vanliga minsta Kvadratberäkningen

OLS-uppskattaren väljer regressionskoefficienterna så att den uppskattade regressionslinjen är så ”nära” som möjligt till de observerade datapunkterna. Här mäts närhet av summan av de kvadrerade misstag som gjorts för att förutsäga $Y$ givet $X$. Låt $b_0$ och $b_1$ vara några uppskattningar av $\beta_0$ och $\beta_1$. Då kan summan av kvadrerade uppskattningsfel uttryckas som

OLS-estimatorn i den enkla regressionsmodellen är paret av estimatorer för avlyssning och lutning vilket minimerar uttrycket ovan. Härledningen av OLS-estimatorerna för båda parametrarna presenteras i bilaga 4.1 till boken. Resultaten sammanfattas i nyckelbegrepp 4.2.

OLS-Uppskattaren, förutsagda värden och rester

OLS-uppskattarna för lutningen $\beta_1$ och avlyssningen $\beta_0$ i den enkla linjära regressionsmodellen är\de OLS-förutsagda värdena $\widehat{y}_i$ och rester $\hat{u}_i$ är\

den uppskattade avlyssningen $\hat{\beta}_0$, lutningsparametern $\hat{\beta}_1$ och resterna $\Left(\hat{u}_i\right)$ beräknas från ett urval av $n$ observationer av $x_i$ och $y_i$, $i$, $…$, $och$. Dessa är uppskattningar av den okända populationen intercept $\left (\beta_0\ right)$, slope $\left (\beta_1\ right)$ och error term$(u_i)$.

formlerna som presenteras ovan kanske inte är mycket intuitiva vid första anblicken. Följande interaktiva program syftar till att hjälpa dig att förstå mekaniken i OLS. Du kan lägga till observationer genom att klicka in i koordinatsystemet där data representeras av punkter. När två eller flera observationer är tillgängliga beräknar applikationen en regressionslinje med hjälp av OLS och viss statistik som visas i den högra panelen. Resultaten uppdateras när du lägger till ytterligare observationer i den vänstra panelen. Ett dubbelklick återställer programmet, dvs alla data tas bort.

det finns många möjliga sätt att beräkna $\hat{\beta}_0$ och $\hat{\beta}_1$ i R. till exempel kan vi implementera formlerna som presenteras i nyckelbegrepp 4.2 med två av R: s mest grundläggande funktioner: medelvärde() och summa(). Innan vi gör det bifogar vi CASchools dataset.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

Calling attach (CASchools) gör det möjligt för oss att adressera en variabel som finns i CASchools med sitt namn: det är inte längre nödvändigt att använda operatören $ i samband med datauppsättningen: R kan utvärdera variabelnamnet direkt.

R använder objektet i användarmiljön om det här objektet delar namnet på variabeln i en bifogad databas. Det är dock en bättre praxis att alltid använda distinkta namn för att undvika sådana (till synes) ambivalenser!

Lägg märke till att vi adresserar variabler som finns i bifogade dataset CASchools direkt för resten av detta kapitel!

naturligtvis finns det ännu mer manuella sätt att utföra dessa uppgifter. Med OLS som en av de mest använda uppskattningsteknikerna innehåller R naturligtvis redan en inbyggd funktion som heter lm() (linjär modell) som kan användas för att utföra regressionsanalys.

det första argumentet för funktionen som ska anges är, liknande plot(), regressionsformeln med den grundläggande syntaxen y ~ x där y är den beroende variabeln och x Den förklarande variabeln. Argumentdata bestämmer datamängden som ska användas i regressionen. Vi återkommer nu exemplet från boken där förhållandet mellan testresultaten och klassstorlekarna analyseras. Följande kod använder lm () för att replikera resultaten som presenteras i figur 4.3 i boken.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

låt oss lägga till den beräknade regressionslinjen till tomten. Den här gången förstorar vi också intervallen för båda axlarna genom att ställa in argumenten xlim och ylim.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)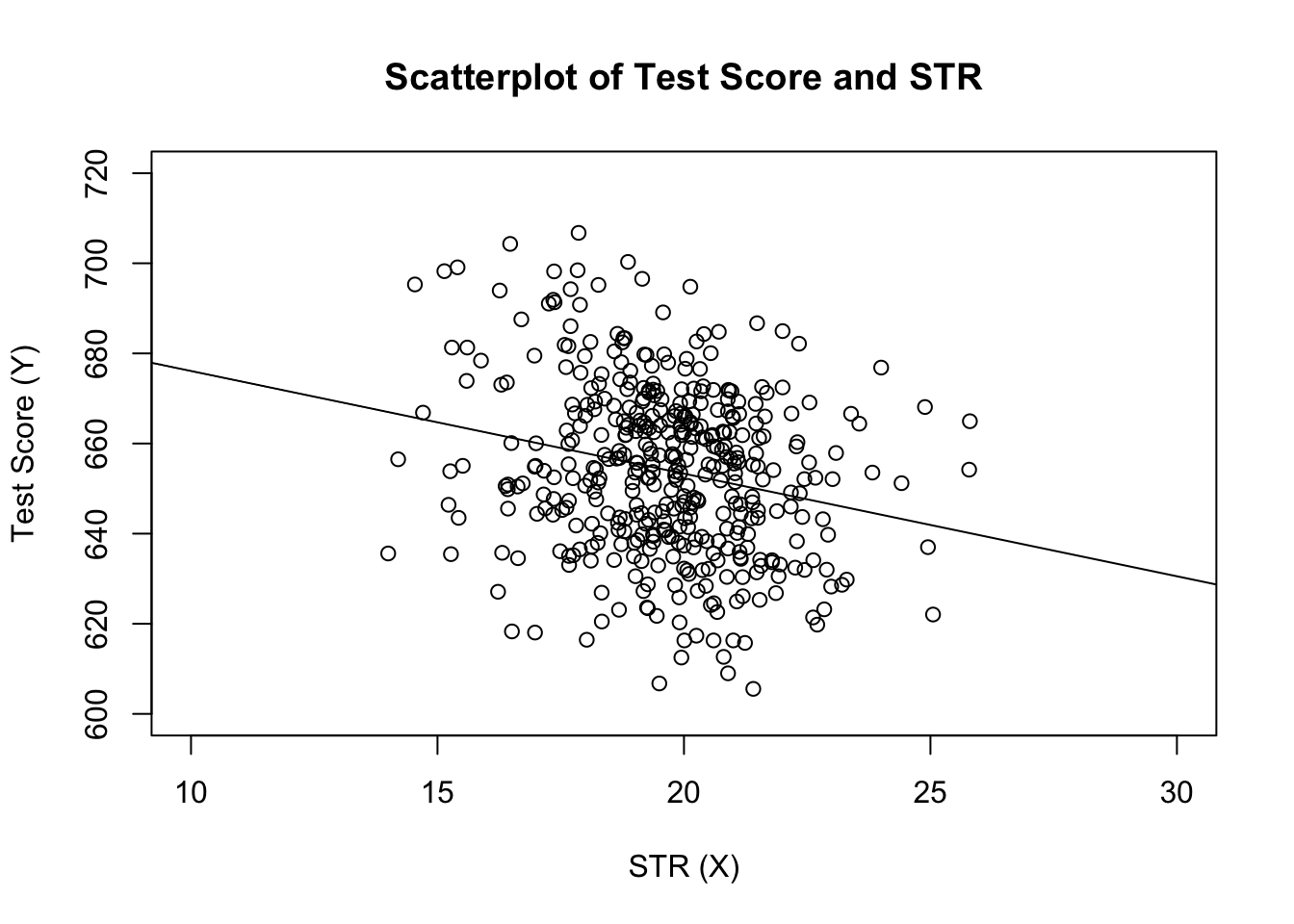

märkte du att den här gången passerade vi inte avlyssnings-och lutningsparametrarna? Om du ringer abline () på ett objekt av klass lm som bara innehåller en enda regressor, r drar regressionslinjen automatiskt!