idag kommer det att bli en kort introduktion till cirkulär statistik (ibland kallad riktningsstatistik). Cirkulär statistik är en intressant indelning av statistik som involverar observationer som vektorer runt en enhetscirkel. Tänk dig att mäta födelsetider på ett sjukhus under en 24-timmarscykel eller riktningsdispersionen hos en grupp flyttande djur. Denna typ av data är involverad i olika områden, såsom ekologi, klimatologi och biokemi. Arten av att mäta observationer runt en enhetscirkel kräver ett annat tillvägagångssätt för hypotesprovning. Fördelningar måste ”lindas” runt cirkeln för att vara till nytta, och konventionella estimatorer som provmedelvärdet eller provvariansen håller inget vatten.
i det här inlägget kommer vi att genomföra Raos Avståndstest för att bedöma enhetligheten hos en cirkulär dataset. Detta är en grundläggande procedur och bör ses som en introduktion till hantering av cirkulära data.
komma igång
vi ska genomföra ett hypotesprov på sköldpaddor, en liten dataset som består av ankomstvinklarna på 10 gröna havssköldpaddor till deras häckande ö. Vårt mål är att avgöra var ankomstvinklarna visar tecken på riktning eller är mer vägledande för en slumpmässig scatter.
installera först paketet circular och fäst sköldpaddans dataset.
install.packages("circular")require(circular)attach(turtles)
plotta data
circular paketet innehåller sin egen plottningsfunktion, plot.circular. Låt oss observera sköldpaddans ankomstvinklar.
plot.circular(arrival)
här är handlingen: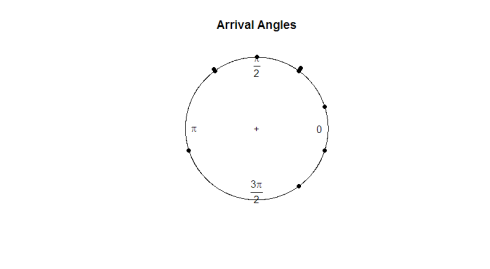
med tanke på ögontestet verkar observationerna vara enhetliga runt cirkeln. Om vi vill köra ett hypotesprov för att avgöra om data verkligen är enhetliga måste vi utveckla en teststatistik som fungerar med vinkeldata.
Vad är en bra parameter för oss att använda? Att ta provmedlet berättar inte mycket om datariktningen (180 grader är inte ett användbart medelvärde på 2 grader och 358 grader). I följande diagram, Observera hur provmedlet inte är till nytta för att representera formen eller spridningen av våra data.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
här är handlingen: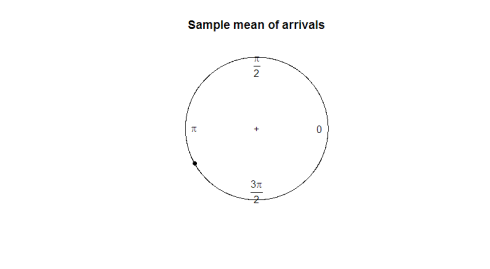
istället kommer vi att använda en metod som bestämmer riktning genom att mäta det genomsnittliga utrymmet mellan observationer. Detta test kallas Raos Avståndstest.
Raos Avståndstest
Raos Avståndstest utvecklades för att bedöma likformigheten hos cirkulära data. Den använder utrymmet mellan observationer för att avgöra om data visar signifikant riktning. Om uppgifterna är enhetliga bör observationer tendera att vara jämnt fördelade.
här är teststatistiken \(U\ ) för Raos Avståndstest: $ $ U = 1/2\sum \ limits_{i=1}^n |t_{i} – 2| $$ där \(2 = 360/n, T_{i} = f_{i+1}-f_{i}\) och \(t_{n} = (360-f_{n}) + f_{1}\)
i grund och botten aggregerar teststatistiken avvikelserna mellan på varandra följande punkter, var och en viktad av det totala antalet observationer i datasetet.
vi kommer att använda funktionen rao.spacing.test() för att köra detta hypotesprov. Vår nollhypotes säger att data har en enhetlig fördelning, medan de alternativa staterna visar data tecken på riktning. Låt oss köra testet.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
med en teststatistik på 127 som faller under det kritiska värdet på 161, misslyckas data att luta sig väsentligt i någon riktning. Vi kan inte avvisa hypotesen att sköldpaddorna ankomster har en jämn fördelning.
slutsats
Raos avståndstest bestämde data för att inte visa några tecken på riktningstrender. Vi kan inte avvisa nollhypotesen om enhetlighet och kommer att anta enhetlighet när det gäller ankomstriktningen. Medan det här inlägget var en relativt grundläggande handledning, har många människor i datavetenskapssamhället inte arbetat med cirkulära data tidigare. Det är ett intressant delämne att dyka in i såväl som ett ungt statistikfält som fortfarande utvecklas.
slutliga anmärkningar
jag skulle vilja förlänga kredit till S. Rao Jammalamadaka PhD, University of California, Santa Barbara, och hans lärobok ”ämnen i cirkulär statistik” för gnistor mitt intresse inom cirkulär statistik.