katamorfismen för antingen är en generalisering av dess veck. Katamorfismen möjliggör operationer som inte är tillgängliga via fold.
denna artikel är en del av en artikelserie om katamorfismer. En katamorfism är en universell abstraktion som beskriver hur man smälter en datastruktur till ett potentiellt mer kompakt värde.
denna artikel presenterar katamorfismen för antingen (även känd som resultat), samt hur man identifierar den. I början av denna artikel presenteras katamarfismen i C#, med exempel. Resten av artikeln beskriver hur man härleder katamarfismen. Denna del av artikeln presenterar mitt arbete i Haskell. Läsare som inte är bekväma med Haskell kan bara läsa den första delen och betrakta resten av artikeln som en valfri bilaga.
antingen är en databehållare som modellerar två ömsesidigt exklusiva resultat. Det används ofta för att returnera värden som kan vara antingen korrekta (höger) eller felaktiga (vänster). I statiskt typad funktionell programmering med en preferens för totala funktioner, erbjuder antingen ett sanerare, mer rimligt sätt att modellera framgång och felresultat än att kasta undantag.
C # catamorphism #
denna artikel använder kyrkan kodning av antingen. Katamarfismen för antingen är Match – metoden:
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
fram till denna artikel har alla tidigare katamorfier varit ett par gjorda av ett initialvärde och en funktion. Antingen katamorfismen är en generalisering, eftersom det är ett par funktioner. En funktion hanterar fallet där det finns ett vänstervärde, och den andra funktionen hanterar fallet där det finns ett rätt värde. Båda funktionerna måste returnera samma, förenande typ, som ofta är en sträng eller något liknande som kan visas i ett användargränssnitt:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
du ser ofta exempel som ovan som förvandlar både vänster och höger fall till strängar eller något som kan representeras som en förenande svarstyp, men det krävs inte på något sätt. Om du kan komma med en förenande typ kan du konvertera båda fallen till den typen:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
i de två ovanstående exemplen använder du två olika funktioner som båda reducerar respektive Guid och string värden till ett tal. Funktionen som förvandlar Guid värden till ett tal räknar hur många av de hexadecimala siffrorna som är större än eller lika med A (10). Den andra funktionen returnerar helt enkelt längden på string , om den är där. Det exemplet är lite meningsfullt, men metoden Match bryr sig inte om det.
i praktisk användning används antingen ofta för felhantering. Artikeln om kyrkans kodning av antingen innehåller ett exempel.
antingen F-Algebra #
som i föregående artikel använder jag Fix och cata som förklaras i Bartosz Milewskis utmärkta artikel om F-algebror.
medan F-algebror och fasta punkter används mest för rekursiva datastrukturer, kan du också definiera en F-Algebra för en icke-rekursiv datastruktur. Du såg redan ett exempel på det i artiklarna om Boolesk katamorfism och kanske katamorfism. Skillnaden mellan t.ex. kanske värden och antingen är att båda fallen av antingen bär ett värde. Du kan modellera detta som en Functor med både en bärartyp och två typargument för de data som antingen kan innehålla:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
jag valde att ringa ’datatyperna’ l(för vänster) och r (för höger) och bärartypen c (för bärare). Som det också var fallet med BoolF och MaybeF, ignorerar Functor – instansen kartfunktionen eftersom bärartypen saknas från både LeftF – fallet och RightF – fallet. Liksom Functor instanserna för BoolF och MaybeF verkar det som om ingenting händer, men på typnivå är det fortfarande en översättning från EitherF l r c till EitherF l r c1. Inte mycket av en funktion, kanske, men definitivt en endofunctor.
som det också var fallet när man härledde kanske och listar katamorfismer, är Haskell inte så glad över att definiera instanser för en typ som Fix (EitherF l r). För att lösa det problemet kan du introducera en newtype wrapper:
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
du kan definiera Functor, Applicative, Monad, osv. instanser för denna typ utan att tillgripa några funky GHC-tillägg. Tänk på att i slutändan är syftet med all denna kod bara att ta reda på hur katamarfismen ser ut. Denna kod är inte avsedd för faktisk användning.
ett par hjälpfunktioner gör det lättare att definiera EitherFix värden:
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
med dessa funktioner kan du skapa EitherFix värden:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
det är allt du behöver för att identifiera katamarfismen.
Haskell catamorphism #
vid denna tidpunkt har du två av tre element i en F-Algebra. Du har en endofunctor (EitherF l r) och ett objekt c, men du behöver fortfarande hitta en morfism EitherF l r c -> c. Lägg märke till att algebra du måste hitta är den funktion som reducerar funktorn till dess bärartyp c, inte ’datatyperna’ l och r. Det tar lite tid att vänja sig, men det är så katamorfismer fungerar. Detta betyder dock inte att du får ignorera l och r, som du ser.
som i tidigare artiklar, börja med att skriva en funktion som kommer att bli katamarfismen, baserad på cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
medan detta sammanställer, med dess undefined implementeringar, gör det uppenbarligen inte något användbart. Jag tycker dock att det hjälper mig att tänka. Hur kan du returnera ett värde av typen c från fallet LeftF? Du kan skicka ett argument till funktionen eitherF :
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
medan du tekniskt kunde skicka ett argument av typen c till eitherF och sedan returnera det värdet från fallet LeftF, skulle det innebära att du skulle ignorera värdet l. Detta skulle vara felaktigt, så gör istället argumentet en funktion och kalla det med l. På samma sätt kan du hantera fallet RightF på samma sätt:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
det här fungerar. Eftersom cata har typen Functor f => (f a -> a) -> Fix f -> a betyder det att alghar typen f a -> a. När det gäller EitherF drar kompilatorn slutsatsen att funktionen alg har typen EitherF l r c -> c, vilket är precis vad du behöver!
du kan nu se vad bärartypen c är för. Det är den typ som algebra extraherar, och därmed den typ som katamarfismen returnerar.
detta är då katamorfismen för antingen. Som hittills har varit konsekvent är det ett par, men nu tillverkat av två funktioner. Som du har sett upprepade gånger är detta inte den enda möjliga katamarfismen, eftersom du till exempel trivialt kan vända argumenten till eitherF.
jag har valt representationen som visas här eftersom den är isomorf till funktionen either från haskells inbyggda Data.Either-modul, som kallar funktionen ”Fallanalys för typen Either”. Båda dessa funktioner (eitherF och either) motsvarar ovanstående C# Match – metod.
Basis #
du kan implementera de flesta andra användbara funktioner med eitherF. Här är Bifunctor instansen:
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
från den instansen följer Functor – instansen trivialt:
instance Functor (EitherFix l) where fmap = second
på toppen av Functor kan du lägga till Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
Observera att implementeringen <*> liknar implementeringen <*> för MaybeFix. Detsamma gäller för Monad – instansen:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
inte bara är EitherFix Foldable, det är Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
Observera, intressant, att bifoldMap är identisk med eitherF.
Bifoldable instansen gör att du trivialt kan implementera Foldable instansen:
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
du kan hitta närvaron av mempty förbryllande, eftersom bifoldMap (eller eitherF; de är identiska) tar som argument två funktioner. Är mempty en funktion?
Ja, mempty kan vara en funktion. Här är det. Det finns en Monoid instans för någon funktion a -> m, där m är en Monoid instans, och mempty är identiteten för den monoid. Det är den instans som används här.
precis som EitherFix är Bifoldable, det är också Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
du kan bekvämt implementera instansen Traversable baserat på instansen Bitraversable :
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
slutligen kan du implementera konverteringar till och från standardtypen Either, med ana som dubbla av cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
detta visar att EitherFix är isomorf till Either, vilket igen fastställer att eitherF och either är ekvivalenta.
relationer #
i den här serien har du sett olika exempel på katamorfismer av strukturer som inte har några veck, katamorfismer som sammanfaller med veck och nu en katamorfism som är mer allmän än vecket. Introduktionen till serien inkluderade detta diagram:
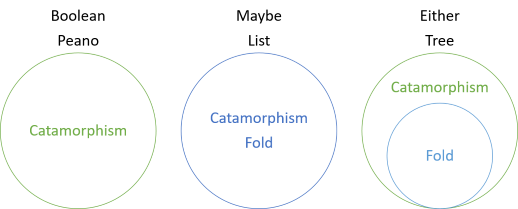
detta visar att booleska värden och Peanotal har katamorfismer, men inga veck, medan för kanske och lista är vikningen och katamorfismen densamma. För båda är dock vecket ett speciellt fall av katamarfismen. Vecket för antingen ’låtsas’ att den vänstra sidan inte existerar. Istället tolkas vänstervärdet som ett saknat högervärde. Således, för att vika antingen värden, du måste ange en ’reserv’ värde som kommer att användas om en antingen värde är inte ett rätt värde:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
i en GHCi-session som ovan kan du skapa två värden av samma typ. Det högra fallet är ett Ordering – värde, medan det vänstra fallet är ett Integer – värde.
med foldr finns det inget sätt att komma åt det vänstra fallet. Medan du kan komma åt och omvandla rätt Ordering – värde, ignoreras numret 42 helt enkelt under veckan. Istället returneras standardvärdet "".
kontrast detta med katamorfismen, som kan komma åt båda fallen:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
i en session som denna återskapar du samma värden, men med hjälp av catamorphism eitherF kan du nu komma åt och omvandla både vänster och höger fall. Med andra ord, katamorfismen gör att du kan utföra operationer som inte är möjliga med vecket.
det är dock intressant att notera att medan vecket är en specialisering av katamorfismen, är bifold identisk med katamorfismen.
sammanfattning #
katamarfismen för antingen är ett par funktioner. En funktion omvandlar det vänstra fodralet, medan den andra funktionen omvandlar det högra fodralet. För något värde kommer endast en av dessa funktioner att användas.
när jag ursprungligen stötte på begreppet katamorfism fann jag det svårt att skilja mellan katamorfism och vikning. Mitt problem var, jag tror, att tutorials jag sprang in mestadels används länkade listor för att visa hur, i så fall, vecket är katamarfismen. Det visar sig dock att detta inte alltid är fallet. En katamarfism är en allmän abstraktion. En vik, å andra sidan, verkar för mig vara mest relaterad till samlingar.
i den här artikeln såg du det första exemplet på en katamarfism som kan göra mer än veckan. För båda är vikningen bara ett speciellt fall av katamarfismen. Du såg dock också hur katamarfismen var identisk med bifold. Således är det fortfarande inte helt klart hur dessa begrepp relaterar. Därför får du i nästa artikel ett exempel på en behållare där det inte finns någon bifold, och där katamarfismen verkligen är en generalisering av veckan.
nästa: Trädkatamorfism.