cunoștințe asumate
elevii vor avea o vastă experiență informală cu geometria în anii anteriori, iar acest lucru va oferi o bună bază intuitivă pentru abordarea mai sistematică a geometriei corespunzătoare în anii 7-10. Subiectele specifice din anii F-6 relevante pentru acest modul sunt:
- utilizarea busolelor și riglelor și desenarea atentă a figurilor geometrice.
- tipuri de unghiuri, inclusiv cel puțin unghiuri drepte, unghiuri acute, unghiuri obtuze și
unghiuri reflexe. - triunghiuri, inclusiv o introducere informală la isoscele și triunghiurile echilaterale.
- patrulatere, inclusiv o introducere informală în pătrate, dreptunghiuri, paralelograme, trapeze și romburi.
- experiență informală cu traduceri, reflecții, rotații și extinderi,
și cu simetrie în contextul unor activități precum plierea unui triunghi isoscel, dreptunghi sau romb.
Motivație
 geometria este folosită pentru a modela lumea din jurul nostru. O vedere a acoperișurilor caselor dezvăluie triunghiuri, trapeze și dreptunghiuri, în timp ce modelele de tigla din trotuare și băi folosesc hexagoane, pentagoane, triunghiuri și pătrate.
geometria este folosită pentru a modela lumea din jurul nostru. O vedere a acoperișurilor caselor dezvăluie triunghiuri, trapeze și dreptunghiuri, în timp ce modelele de tigla din trotuare și băi folosesc hexagoane, pentagoane, triunghiuri și pătrate.
Constructorii, tilerii, arhitecții, designerii grafici și designerii web folosesc în mod obișnuit idei geometrice în munca lor. Clasificarea unor astfel de obiecte geometrice și studierea proprietăților lor sunt foarte importante. Geometria are, de asemenea, multe aplicații în artă.
la fel cum aritmetica are numere ca obiecte de bază de studiu, la fel punctele, liniile și cercurile sunt elementele de bază ale geometriei plane.
în geometria școlii secundare, începem cu o serie de idei intuitive (puncte, linii și unghiuri) care nu sunt deloc ușor de definit cu precizie, urmate de unele definiții (unghiuri opuse vertical, linii paralele etc.) și din acestea deducem fapte importante, care sunt adesea denumite teoreme. În învățământul secundar, nivelul de rigoare ar trebui să se dezvolte lent de la un an la altul, dar în fiecare etapă stabilirea clară este foarte importantă și ar trebui subliniată.
astfel, geometria oferă studenților posibilitatea de a-și dezvolta intuiția geometrică, care are aplicații în multe domenii ale vieții și, de asemenea, de a învăța cum să construiască argumente logice și să facă deducții într-un cadru care este, în cea mai mare parte, independent
de număr.
conținut
puncte și linii
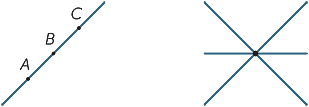
cele mai simple obiecte din geometria plană sunt punctele și liniile. Deoarece sunt atât de simple, este greu să le oferim definiții precise, așa că, în schimb, ne propunem să oferim elevilor o descriere aproximativă a proprietăților lor care sunt în conformitate cu intuiția noastră. Un punct marchează o poziție, dar nu are Dimensiune. În practică, atunci când tragem un punct, acesta are în mod clar o lățime definită, dar reprezintă un punct în imaginația noastră. O linie nu are lățime și se extinde infinit în ambele direcții. Când tragem o linie are lățime și are capete, deci nu este cu adevărat o linie, ci reprezintă o linie în imaginația noastră. Având în vedere două puncte distincte A și B, atunci există o linie (și o singură) care trece prin ambele puncte. Folosim majuscule pentru a ne referi la puncte și linii de nume fie prin menționarea a două puncte pe Linie, fie prin utilizarea literelor mici, cum ar fi  și m. astfel, linia dată de mai jos este denumită linia AB sau linia
și m. astfel, linia dată de mai jos este denumită linia AB sau linia  .
.

având în vedere două linii distincte, există două posibilități: fie se pot întâlni într-un singur punct, fie nu se pot întâlni niciodată, indiferent cât de departe sunt extinse (sau produse). Liniile care nu se întâlnesc niciodată sunt numite paralele. În a doua diagramă, scriem AB / / CD.
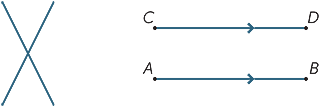
trei (sau mai multe) puncte care se află pe o linie dreaptă se numesc coliniare.
trei (sau mai multe) linii care se întâlnesc într-un singur punct sunt numite concurente.
|
|
|
| coliniare |
concurente |
Exercițiul 1
desenați trei linii care nu sunt concurente, astfel încât să nu existe două paralele.
Exercițiul 2
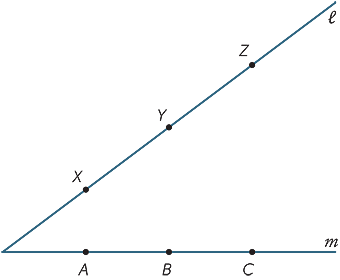
faceți o copie mare a diagramei de mai jos. Punctele X, Y, Z sunt orice puncte de pe linia  și A, B, C sunt orice puncte de pe linia m. Alăturați-vă AY și XB își numesc intersecția R. Alăturați-vă BZ și YC și apelați intersecția lor P. Alăturați-vă CX și ZA și apelați intersecția lor Q. ce observați despre punctele P, Q, R? (Acest rezultat se numește teorema lui Pappus, c. 340 D.hr.)
și A, B, C sunt orice puncte de pe linia m. Alăturați-vă AY și XB își numesc intersecția R. Alăturați-vă BZ și YC și apelați intersecția lor P. Alăturați-vă CX și ZA și apelați intersecția lor Q. ce observați despre punctele P, Q, R? (Acest rezultat se numește teorema lui Pappus, c. 340 D.hr.)
intervale, raze și unghiuri
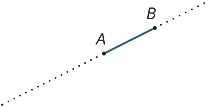 să presupunem că A și B sunt două puncte pe o linie. Intervalul
să presupunem că A și B sunt două puncte pe o linie. Intervalul
AB este partea liniei dintre a și B, incluzând cele două puncte finale.
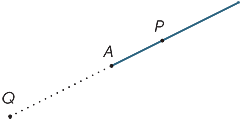 punctul A din diagramă împarte linia în două bucăți numite raze. Raza AP este acea rază care conține punctul P (și punctul A).
punctul A din diagramă împarte linia în două bucăți numite raze. Raza AP este acea rază care conține punctul P (și punctul A).
Unghiuri
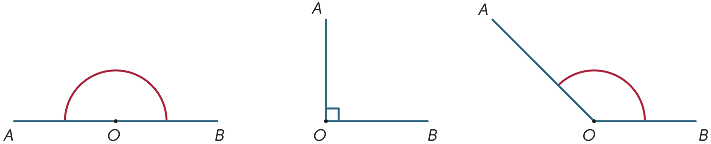
 în diagramă, regiunea umbrită dintre razele OA și OB se numește unghiul AOB sau unghiul BOA. Semnul unghiului
în diagramă, regiunea umbrită dintre razele OA și OB se numește unghiul AOB sau unghiul BOA. Semnul unghiului ![]() este scris astfel încât să scriem
este scris astfel încât să scriem ![]() AOB.
AOB.
 regiunea umbrită din exterior se numește unghiul reflex format de OA și OB. De cele mai multe ori, dacă nu specificăm cuvântul reflex, toate unghiurile noastre se referă la zona dintre raze și nu în afara lor.
regiunea umbrită din exterior se numește unghiul reflex format de OA și OB. De cele mai multe ori, dacă nu specificăm cuvântul reflex, toate unghiurile noastre se referă la zona dintre raze și nu în afara lor.
dimensiunea unui unghi
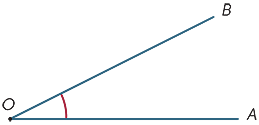 Imaginați-vă că raza OB este rotită în jurul punctului O până când se află de-a lungul OA. Cantitatea de rotire se numește dimensiunea unghiului AOB. Putem defini în mod similar dimensiunea unghiului reflex.
Imaginați-vă că raza OB este rotită în jurul punctului O până când se află de-a lungul OA. Cantitatea de rotire se numește dimensiunea unghiului AOB. Putem defini în mod similar dimensiunea unghiului reflex.
vom folosi de multe ori litere mici grecesti,… pentru a reprezenta dimensiunea unui unghi.
dimensiunea unghiului corespunzător unei revoluții complete a fost împărțită (de babilonieni) în 360 de părți egale, pe care le numim grade. (Probabil au ales 360, deoarece era aproape de numărul de zile dintr-un an.) Prin urmare, dimensiunea unui unghi drept este de 180%, iar dimensiunea unui unghi drept este de 90%. Alte unghiuri pot fi măsurate (aproximativ) folosind un raportor.
|
|
||
| unghi drept | unghi drept |
unghi obtuz |
unghiurile sunt clasificate în funcție de mărimea lor. Spunem că un unghi cu dimensiunea α este acută
(un cuvânt care înseamnă ‘ascuțit’) dacă 0° < α < 90°, α este obtuz (un cuvânt care înseamnă ‘tocit’) dacă
90° < α < 180° și α este reflex dacă 180° < α < 360°.
deoarece protractorul are două scale, elevii trebuie să fie atenți la desen și
măsurarea unghiurilor. Este un exercițiu util să folosiți un raportor pentru a desena câteva unghiuri, cum ar fi 30°, 78°, 130°, 163°.
Exercițiu 3
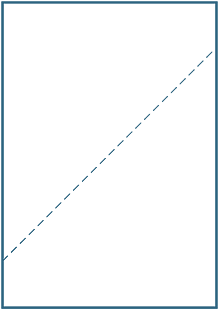 îndoiți o foaie de hârtie A4 care se potrivește cu colțurile opuse (în diagonală). Desenați o linie de-a lungul pliului care se formează și măsurați unghiurile dintre pliu și lateral.
îndoiți o foaie de hârtie A4 care se potrivește cu colțurile opuse (în diagonală). Desenați o linie de-a lungul pliului care se formează și măsurați unghiurile dintre pliu și lateral.
în exercițiul de mai sus, cele două unghiuri formează împreună o linie dreaptă și astfel se adaugă la 180 de metri cubi. Două unghiuri care se adaugă la 180 de Centimetre se numesc unghiuri suplimentare; astfel, 45 de Centimetre și 135 de Centimetre sunt unghiuri suplimentare.
se numesc două unghiuri complementare care se adaugă la 90 de centimetrii; astfel, 23 de centimetrii și 67 de centimetrii sunt
unghiuri la un punct
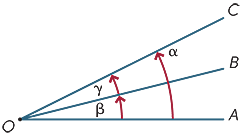 se spune că două unghiuri la un punct sunt adiacente dacă împărtășesc o rază comună. Prin urmare, în diagramă,
se spune că două unghiuri la un punct sunt adiacente dacă împărtășesc o rază comună. Prin urmare, în diagramă, ![]() AOB și
AOB și ![]() BOC sunt adiacente.
BOC sunt adiacente.
unghiurile adiacente pot fi adăugate, astfel încât în diagrama
XLC = XLC + XLC.
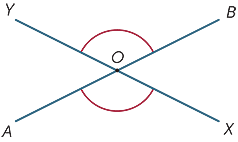
când două linii se intersectează, se formează patru unghiuri în punctul de intersecție.
în diagramă, unghiurile marcate ![]() AOX și
AOX și ![]() BOY sunt numite vertical opuse.
BOY sunt numite vertical opuse.
 din
din
-
 AOX este suplimentul cutiei
AOX este suplimentul cutiei  (unghi drept).
(unghi drept). -
 băiatul este, de asemenea, suplimentul cutiei
băiatul este, de asemenea, suplimentul cutiei  (unghi drept),
(unghi drept),
putem concluziona că aceste unghiuri opuse vertical,![]() AOX și
AOX și ![]() BOY sunt egale. Avem astfel prima noastră declarație geometrică importantă
BOY sunt egale. Avem astfel prima noastră declarație geometrică importantă
:
unghiurile opuse vertical sunt egale.
un rezultat în geometrie (și în matematică în general) este adesea numit teoremă. O teoremă este o afirmație importantă care poate fi dovedită prin deducție logică. Argumentul de mai sus este o dovadă a teoremei; uneori dovezile sunt prezentate formal după enunțul teoremei.
 dacă două linii se intersectează astfel încât toate cele patru unghiuri să fie unghiuri drepte, atunci se spune că liniile sunt perpendiculare.
dacă două linii se intersectează astfel încât toate cele patru unghiuri să fie unghiuri drepte, atunci se spune că liniile sunt perpendiculare.
unghiuri la un punct – argumente geometrice
următoarele motive pot fi utilizate în argumente geometrice:
- unghiurile adiacente pot fi adăugate sau scăzute.
- unghiurile într-o revoluție se adaugă la 360 inkt.
- unghiurile în linie dreaptă se adaugă la 180 de milimetri.
- unghiurile opuse vertical sunt egale.
transversale și linii paralele
 o linie transversală este o linie care întâlnește alte două linii.
o linie transversală este o linie care întâlnește alte două linii.
unghiuri corespunzătoare
diferite unghiuri sunt formate de transversal. În diagramele de mai jos, cele două unghiuri marcate sunt numite unghiuri corespunzătoare.
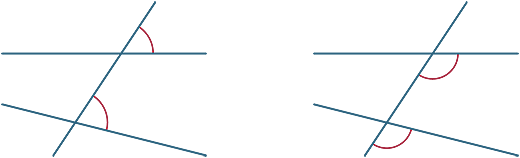
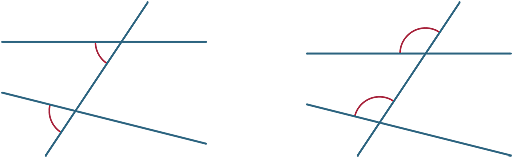
 acum ne uităm la ce se întâmplă atunci când cele două linii tăiate de transversal sunt paralele.
acum ne uităm la ce se întâmplă atunci când cele două linii tăiate de transversal sunt paralele.
Inituitively, dacă unghiul α este mai mare decât β apoi CD-ar trece AB la stânga lui F și dacă ar fi fost mai puțin decât β, că va trece la dreapta lui F. Deci, din moment ce liniile nu trece deloc, α poate fi nici mai putin nici mai mult de β și deci este egal cu β.
în mod alternativ, imaginați-vă traducerea unghiului QGD de-a lungul GF până când G coincide cu F. deoarece liniile sunt paralele, ne-am aștepta ca unghiul XV să coincidă cu unghiul XV. Această observație ne conduce la presupunerea că:
unghiurile corespunzătoare formate din linii paralele sunt egale.
nu putem dovedi acest rezultat, deși am arătat că este plauzibil din punct de vedere geometric. O vom accepta ca o axiomă a geometriei. O axiomă este o afirmație pe care nu o putem dovedi, dar care este intuitiv rezonabilă. Rețineți că multe dintre faptele pe care le-am afirmat deja, cum ar fi: pot fi adăugate unghiuri adiacente, iar două puncte determină o linie etc., sunt, de asemenea, axiome, deși nu le-am declarat în mod explicit în acest fel.
unghiuri Alternative
în fiecare diagramă, cele două unghiuri marcate sunt numite unghiuri alternative (deoarece sunt pe laturi alternative ale transversalului).

 dacă liniile AB și CD sunt paralele, atunci unghiurile alternative sunt egale. Acest rezultat poate fi acum dovedit.
dacă liniile AB și CD sunt paralele, atunci unghiurile alternative sunt egale. Acest rezultat poate fi acum dovedit.
![]() DGQ = Irak (unghiuri corespunzătoare, AB / / CD)
DGQ = Irak (unghiuri corespunzătoare, AB / / CD)
![]() DGQ = (unghiuri opuse pe verticală la G)
DGQ = (unghiuri opuse pe verticală la G)
deci,.
pentru a rezuma:
unghiurile Alternative formate din linii paralele sunt egale.
unghiuri Co-interioare
în cele din urmă, în fiecare diagramă de mai jos, cele două unghiuri marcate sunt numite unghiuri co-interioare și se află pe aceeași parte a transversalului.

dacă liniile AB și CD sunt paralele, atunci este evident că unghiurile co-interioare nu sunt egale, dar se dovedește că acestea sunt suplimentare, adică suma lor este de 180 de la sută .
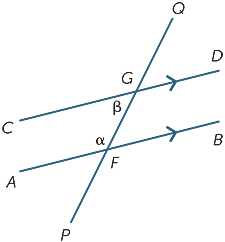 acesta este un rezultat care este, de asemenea, ușor de dovedit:
acesta este un rezultat care este, de asemenea, ușor de dovedit:
![]() BFG = XV (unghiuri alternative, AB ||CD)
BFG = XV (unghiuri alternative, AB ||CD)
000%)
180% (unghi drept la F)
pentru a rezuma:
sunt suplimentare unghiurile Co-interioare formate din linii paralele.
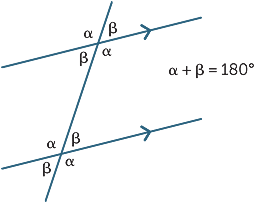 cele trei rezultate pot fi rezumate
cele trei rezultate pot fi rezumate
prin următoarea diagramă:
exemple numerice
având în vedere informațiile despre unghiurile dintr-o diagramă, putem folosi rezultatele de mai sus pentru a găsi dimensiunea altor unghiuri din diagramă. Aceasta este o abilitate simplă, dar foarte importantă, adesea menționată informal ca urmărirea unghiului. În rezolvarea problemelor, succesiunea pașilor nu este întotdeauna unică. Pot exista mai multe abordări diferite, dar la fel de valabile.
de exemplu, în diagrama următoare, căutăm dimensiunea unghiului BAC.

![]() DCA = 102 (unghiuri alternative, ac / BD)
DCA = 102 (unghiuri alternative, ac / BD)
![]() BAC = 78 (co-unghiuri interioare, AB / / CD)
BAC = 78 (co-unghiuri interioare, AB / / CD)
Exercițiul 4
utilizați o secvență alternativă de pași pentru a găsi ![]() BAC.
BAC.
Exercițiu 5
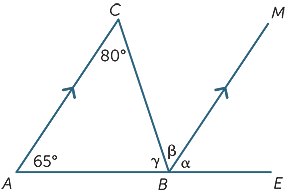 folosind doar proprietățile liniilor paralele, găsiți (cu motive) unghiurile lipsă din diagrama următoare.
folosind doar proprietățile liniilor paralele, găsiți (cu motive) unghiurile lipsă din diagrama următoare.
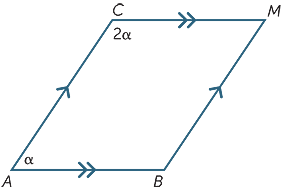
exercitiul 6
găsiți valoarea lui inqq în diagrama următoare.
declarații Converse
multe afirmații din matematică au un invers, în care implicația merge în direcția opusă. De exemplu, afirmația
‘fiecare număr par se termină în 0, 2, 4, 6 sau 8.’
are converse
‘ fiecare număr care se termină în 0, 2, 4, 6 sau 8 este egal.’
această afirmație particulară și conversa ei sunt ambele adevărate, dar acest lucru nu este în niciun caz întotdeauna
cazul.
de exemplu, următoarele două afirmații sunt conversații între ele:
‘fiecare multiplu de 4 este un număr par.’
‘ fiecare număr par este un multiplu de 4.’
și aici, prima afirmație este adevărată, dar a doua este falsă.
exercițiul 7
notează:
a![]() o afirmație geometrică adevărată a cărei conversă este de asemenea adevărată,
o afirmație geometrică adevărată a cărei conversă este de asemenea adevărată,
b![]() afirmație geometrică falsă a cărei conversă este adevărată,
afirmație geometrică falsă a cărei conversă este adevărată,
c![]() o afirmație geometrică falsă a cărei conversă este de asemenea falsă.
o afirmație geometrică falsă a cărei conversă este de asemenea falsă.
teoremele Converse pentru linii paralele
am văzut că unghiurile corespunzătoare formate din linii paralele sunt egale. Putem scrie declarația converse după cum urmează.
declarație :dacă liniile sunt paralele, atunci unghiurile corespunzătoare sunt egale.
Converse: Dacă unghiurile corespunzătoare sunt egale, atunci liniile sunt paralele.
enunțul converse este de asemenea adevărat și este adesea folosit pentru a demonstra că două linii sunt paralele. Același lucru este valabil și în ceea ce privește unghiurile alternative și co-interioare.
declarație :dacă liniile sunt paralele, atunci unghiurile alternative sunt egale.
Converse: dacă unghiurile alternative sunt egale, atunci liniile sunt paralele.
declarație :dacă liniile sunt paralele, atunci unghiurile co-interioare sunt suplimentare.
Converse: Dacă unghiurile co-interioare sunt suplimentare, atunci liniile sunt paralele.
astfel, în fiecare diagramă, liniile AB și CD sunt paralele.

exercițiu 8
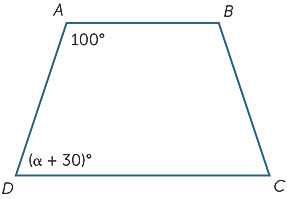 ce valoare a lui XV va face AB paralel cu CD-ul?
ce valoare a lui XV va face AB paralel cu CD-ul?
dovezi ale celor trei conversații
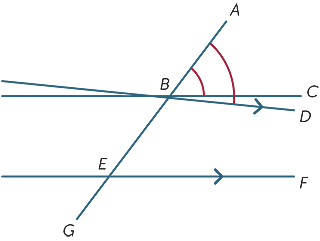 presupunem că unghiurile corespunzătoare formate de transversal sunt egale și arătăm că liniile sunt paralele.
presupunem că unghiurile corespunzătoare formate de transversal sunt egale și arătăm că liniile sunt paralele.
în diagramă, presupunem că ![]() ABC =
ABC = ![]() BEF.
BEF.
dacă BC și EF nu sunt paralele, atunci trageți
bd paralel cu EF.
acum, deoarece BD și EF sunt paralele ![]() ABD =
ABD = ![]() BEF și deci
BEF și deci ![]() ABC =
ABC = ![]() ABD ceea ce este clar imposibil decât dacă liniile BC și BD sunt aceleași. Prin urmare, liniile BC și EF sunt paralele.
ABD ceea ce este clar imposibil decât dacă liniile BC și BD sunt aceleași. Prin urmare, liniile BC și EF sunt paralele.
celelalte dovezi urmează în același mod.
exercițiul 9
dă o dovadă a celei de-a doua teoreme converse (unghiuri alternative).
suma unghiului unui triunghi
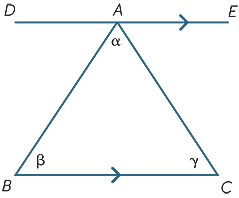 rezultatele din secțiunea anterioară pot fi folosite pentru a deduce unul dintre cele mai importante fapte din geometrie − suma unghiului unui triunghi este de 180%.
rezultatele din secțiunea anterioară pot fi folosite pentru a deduce unul dintre cele mai importante fapte din geometrie − suma unghiului unui triunghi este de 180%.
incepem cu triunghiul ABC cu unghiurile de la Inox. Desenați linia DAE paralelă cu BC. Atunci,
![]() DAB = (unghiuri alternative, BC||de)
DAB = (unghiuri alternative, BC||de)
![]() EAC = (unghiuri alternative, BC||DE)
EAC = (unghiuri alternative, BC||DE)
+ + 180 (unghi drept).
astfel, am dovedit teorema
suma unghiurilor dintr-un triunghi este de 180 inkt.
un patrulater este o figură plană delimitată de patru laturi.
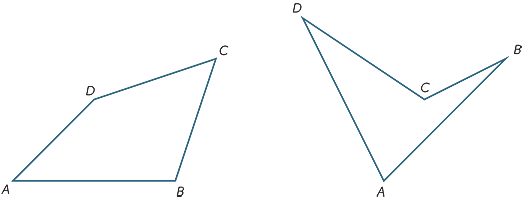
exercițiul 10
împărțind patrulaterul ABCD în două triunghiuri, găsiți suma unghiurilor.
link-uri înainte
materialul din acest modul a început să plaseze geometria pe o bază rezonabilă sistematică a obiectelor atent definite, axiome care trebuie asumate și teoreme pe care le-am dovedit. Pe această bază, putem dezvolta o relatare sistematică a geometriei plane care implică:
- teorema lui Pitagora
- congruență și triunghiuri congruente
- similaritate și triunghiuri similare
- isoscele și triunghiurile echilaterale
- patrulatere speciale, inclusiv pătrate, dreptunghiuri, paralelograme, romburi și trapeze
- geometria cercurilor.
geometria planului va fi, de asemenea, fundamentală în multe alte domenii ale matematicii anilor 7-10:
- transformări
- geometrie tridimensională
- zone și volume
- trigonometrie
- geometrie de coordonate
- graficele cercurilor și parabolelor.
ideile tangentelor și zonelor conduc la rândul lor la calcul în anii 11-12.
Istorie și aplicații
Istorie
construcțiile incredibile ale piramidelor și templele uriașe ale Egiptului dezvăluie că egiptenii trebuie să fi avut o foarte bună cunoaștere și înțelegere a geometriei de bază, cel puțin la nivel practic. Pe de altă parte, nu există dovezi că ar fi sistematizat aceste cunoștințe într-un mod formal. Acest lucru a fost lăsat la grecii antici. Nu avem cunoștințe detaliate despre această sistematizare, cu excepția afirmației că Thales (cca. 624 Î. HR. – cca. 546 î.HR.) a dat primele dovezi ale faptelor geometrice care au marcat începuturile geometriei deductive. Școala pitagoreană a continuat această lucrare, iar Platon (428 Î.HR. -348 Î. HR.) se bazează în mod clar pe opera matematicienilor anteriori când menționează fapte geometrice în scrierile sale. Dialogul geometric din opera sa Meno, în care Socrate îl face pe un băiat sclav să ajungă la o teoremă geometrică printr-o serie de deducții logice, merită citit. Dacă originile geometriei sunt neclare, produsul final nu este. Euclid (323-283 Î.hr.), scriind în Alexandria, a produs o lucrare remarcabilă, numită elementele, care a rămas manualul standard în geometrie pentru mai mult de 2000 de ani. În această lucrare, Euclid stabilește o serie de definiții (cum ar fi pentru puncte și linii), postulate și Noțiuni comune. (Aceste zile le numim axiome.) Din acestea, el a dezvoltat logic, într-o ordine foarte atent aleasă, o mulțime de teoreme la care ne referim în general ca geometrie euclidiană. Există o serie de alte rezultate geometrice, cum ar fi teorema lui Pappus, care au fost descoperite după Euclid, dar acestea nu sunt în general acoperite în școala secundară.
unul dintre cele cinci postulate ale lui Euclid nu era atât de evident adevărat pe cât păreau celelalte. O versiune a acesteia, cunoscută sub numele de Axioma lui Playfair afirmă că: Având în vedere o linie  și un punct P, nu pe
și un punct P, nu pe  , există o singură linie paralelă cu
, există o singură linie paralelă cu  care trece prin P. în secolul al 19-lea, un număr de matematicieni au pus întrebarea ‘ce se întâmplă dacă negăm acest postulat? Acest lucru se face presupunând că fie nu există o astfel de linie paralelă, fie spunând că există mai multe astfel de linii. Acest lucru a dus la dezvoltarea geometriilor non-euclidiene, dintre care una s-a dovedit a oferi unul dintre modelele bune pentru univers.
care trece prin P. în secolul al 19-lea, un număr de matematicieni au pus întrebarea ‘ce se întâmplă dacă negăm acest postulat? Acest lucru se face presupunând că fie nu există o astfel de linie paralelă, fie spunând că există mai multe astfel de linii. Acest lucru a dus la dezvoltarea geometriilor non-euclidiene, dintre care una s-a dovedit a oferi unul dintre modelele bune pentru univers.
Aplicații
într − un sens foarte real, geometria și intuiția geometrică formează fundamentele tuturor
matematicii − geometria duce la geometria coordonată care duce la calcul și
toate numeroasele sale aplicații-și astfel este crucială în curriculum.
la un nivel mai practic, Constructorii, inspectorii, inginerii și arhitecții au fost utilizatori grei ai geometriei și ideilor geometrice de secole. Mai recent, odată cu dezvoltarea computerelor, artiștii grafici și designerii web s-au alăturat acestui grup de oameni care au nevoie și folosesc geometria în munca lor. Când a fost întrebat recent cât de utilă este geometria, Jim Kelly, un om de știință aplicat a spus: … geometria este o parte importantă a proiectării, desenului și modelării pe calculator. De asemenea, este utilizat frecvent în … fizică și alte cursuri de științe fizice ca parte a înțelegerii efectelor sarcinilor asupra structurilor și punctelor de echilibrare(centre de greutate) pentru solidele compozite. În chimie, înțelegerea geometriei unei molecule este legată de înțelegerea proprietăților substanțelor. Există multe alte exemple. (de pe site-ul Ask A Scientist.)
o istorie a matematicii: O introducere, ediția a 3-a, Victor J. Katz, Addison-Wesley, (2008)
Istoria matematicii, D. E. Smith, Dover publications New York, (1958)
răspunsuri la exerciții
exercițiu 1
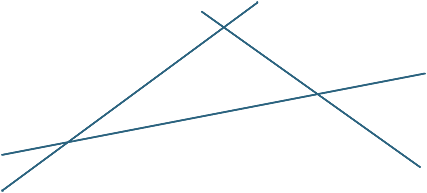
EXERCITIUL 2
punctele sunt coliniare
EXERCIȚIU 3
60°
EXERCIȚIU 4
![]() DBA = 102° (unghiuri corespondente, AB||CD)
DBA = 102° (unghiuri corespondente, AB||CD)
![]() BAC = 78° (co-unghiuri interioare, AC||BD)
BAC = 78° (co-unghiuri interioare, AC||BD)
EXERCITIUL 5
α = 65°![]() (unghiuri corespondente, AC||BM)
(unghiuri corespondente, AC||BM)
β = 80°![]() (unghiuri alterne, AC||BM)
(unghiuri alterne, AC||BM)
γ + β = 115°![]() (co-unghiuri interioare, AC||BM)
(co-unghiuri interioare, AC||BM)
prin Urmare, γ = 35°
(Aceasta este structura pentru o dovadă a rezultat că suma unghi al unui triunghi este de 180°)
exercitiul 6
XV = 60
exercitiul 7
a ![]() un patrulater cu fiecare dintre unghiurile sale interioare un unghi drept este un dreptunghi.
un patrulater cu fiecare dintre unghiurile sale interioare un unghi drept este un dreptunghi.
Converse: fiecare unghi interior al unui dreptunghi este un unghi drept.
b![]() un dreptunghi este un pătrat
un dreptunghi este un pătrat
Converse: un pătrat este un dreptunghi
c![]() suma unghiulară a unghiurilor interioare ale unui triunghi este de 200%
suma unghiulară a unghiurilor interioare ale unui triunghi este de 200%
Converse: un poligon pentru care suma unghiului interior este de 200% este un triunghi.
exercitiul 8
OLX = 50 OLX
exercitiul 9
ne referim la aceeasi diagrama.
așezați un punct H pe linia EF din stânga E.
![]() CBE =
CBE = ![]() BEH
BEH
dacă BC și EF nu sunt paralele, trageți bd paralel cu EF.
deoarece BD și EF sunt paralele, ![]() EBD=
EBD= ![]() BEH, ceea ce este clar imposibil dacă liniile BC și BD nu sunt aceleași.
BEH, ceea ce este clar imposibil dacă liniile BC și BD nu sunt aceleași.
prin urmare, liniile BC și EF sunt paralele.
exercițiu 10
360°
proiectul îmbunătățirea educației matematice în școli (TIMES) 2009-2011 a fost finanțat de Departamentul Guvernului Australian pentru educație, ocuparea forței de muncă și Relații la locul de muncă.
opiniile exprimate aici sunt cele ale autorului și nu reprezintă în mod necesar punctele de vedere ale Departamentului guvernului Australian de educație, ocuparea forței de muncă și Relații la locul de muncă.
Universitatea din Melbourne, în numele Centrului Internațional de Excelență pentru educație în matematică (ICE-EM), Divizia de educație a Institutului Australian de științe Matematice (AMSI), 2010 (cu excepția cazului în care se indică altfel). Această operă este pusă la dispoziție sub licența Creative Commons Atribuire-Necomercial-NoDerivs 3.0 Unported.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()