astăzi va fi o scurtă introducere în Statisticile circulare (uneori denumite statistici direcționale). Statistica circulară este o subdiviziune interesantă a statisticilor care implică observații luate ca vectori în jurul unui cerc unitar. De exemplu, imaginați-vă măsurarea timpilor de naștere la un spital pe un ciclu de 24 de ore sau dispersia direcțională a unui grup de animale migratoare. Acest tip de date este implicat într-o varietate de domenii, cum ar fi ecologia, climatologia și biochimia. Natura măsurării observațiilor în jurul unui cerc unitar necesită o abordare diferită a testării ipotezelor. Distribuțiile trebuie să fie” înfășurate ” în jurul cercului pentru a fi utile, iar estimatorii convenționali, cum ar fi media eșantionului sau varianța eșantionului, nu dețin apă.
în acest post, vom efectua testul de spațiere Rao pentru a evalua uniformitatea unui set de date circular. Aceasta este o procedură de bază și ar trebui gândită ca o introducere în manipularea datelor circulare.
Noțiuni de bază
vom efectua un test de ipoteză pe broaște țestoase, un mic set de date format din unghiurile de sosire a 10 broaște țestoase verzi pe insula lor cuibăritoare. Scopul nostru este de a determina unde unghiurile de sosire prezintă semne de direcționalitate sau sunt mai indicative pentru o împrăștiere aleatorie.
mai întâi, instalați pachetul circular și atașați setul de date turtles.
install.packages("circular")require(circular)attach(turtles)
trasarea datelor
pachetul circular conține propria sa funcție de trasare, plot.circular. Să observăm unghiurile de sosire ale țestoaselor.
plot.circular(arrival)
Iată complotul: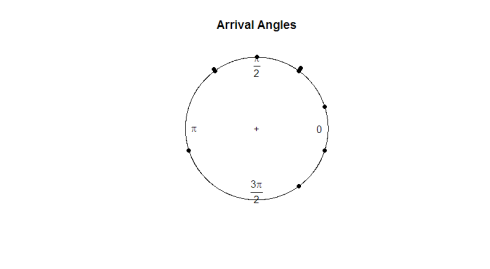
având în vedere testul ocular, observațiile par a fi uniforme în jurul cercului. Dacă dorim să rulăm un test de ipoteză pentru a determina dacă datele sunt cu adevărat uniforme, va trebui să dezvoltăm o statistică de testare care să funcționeze cu date unghiulare.
ce este un parametru bun pentru noi de a utiliza? Luând media eșantionului nu ne spune prea multe despre direcția datelor (180 de grade nu este o medie utilă de 2 grade și 358 de grade). În graficul următor, observați cum media eșantionului nu are niciun folos în reprezentarea formei sau răspândirii datelor noastre.
mean(arrival)plot.circular(mean(arrival)) 0.9120794
Iată complotul: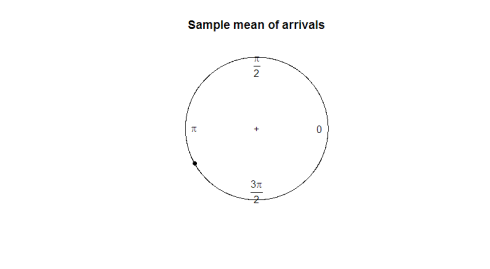
în schimb, vom folosi o metodă care determină direcționalitatea prin măsurarea spațiului mediu dintre observații. Acest test se numește testul spațierii lui Rao.
testul de spațiere Rao
testul de spațiere Rao a fost dezvoltat pentru a evalua uniformitatea datelor circulare. Folosește spațiul dintre observații pentru a determina dacă datele prezintă o direcționalitate semnificativă. Dacă datele sunt uniforme, observațiile ar trebui să aibă tendința de a fi distanțate uniform.
aici este statistica de testare \(U\) pentru testul spațiere Rao lui: $ $ U = 1/2 \ sum \ limits_{i=1}^n| t_{i} – inqu/ $ $ în cazul în care \(inqu = 360 / n, T_{i} = f_{i+1}-f_{i}\) și \(t_{n} = (360-f_{n}) + f_{1}\)
practic, statistica testului agregă abaterile dintre punctele consecutive, fiecare ponderat cu numărul total de observații din setul de date.
vom folosi funcția rao.spacing.test() pentru a rula acest test de ipoteze. Ipoteza noastră nulă spune că datele au o distribuție uniformă, în timp ce Statele alternative arată că datele prezintă semne de direcționalitate. Să facem testul.
rao.spacing.test(arrival,alpha=.10) Rao's Spacing Test of Uniformity Test Statistic = 127.2689 Level 0.1 critical value = 161.23 Do not reject null hypothesis of uniformity
cu o statistică a testului de 127 care scade sub valoarea critică a 161, datele nu se înclină semnificativ în nicio direcție. Nu putem respinge ipoteza că sosirile țestoaselor au o distribuție uniformă.
concluzie
testul de spațiere al Rao a determinat datele să nu prezinte semne de tendințe direcționale. Nu putem respinge ipoteza nulă a uniformității și ne vom asuma uniformitatea în ceea ce privește direcția de sosire. În timp ce această postare a fost un tutorial relativ de bază, mulți oameni din comunitatea științei datelor nu au mai lucrat cu date circulare înainte. Este un subtopic interesant pentru a se arunca cu capul în, precum și un domeniu tânăr de statistici, care este încă în evoluție.
observații finale
aș dori să acorde credit S. Rao Jammalamadaka PhD, de la Universitatea din California, Santa Barbara, și manualul său „subiecte în Statistica circulară” pentru ceea ce a dus interesul meu în domeniul statisticii circulare.