4.2 estimarea coeficienților modelului de regresie liniară / Introducere în econometrie cu R

4.2 estimarea coeficienților modelului de regresie liniară

în practică, interceptarea $\beta_0$ și panta $\beta_1$ a liniei de regresie a populației sunt necunoscute. Prin urmare, trebuie să folosim date pentru a estima ambii parametri necunoscuți. În cele ce urmează, un exemplu din lumea reală va fi folosit pentru a demonstra modul în care se realizează acest lucru. Vrem să corelăm scorurile testelor cu raporturile elev-profesor măsurate în școlile californiene. Scorul testului este media la nivel de district a scorurilor de citire și matematică pentru elevii de clasa a cincea. Din nou, dimensiunea clasei este măsurată ca numărul de elevi împărțit la numărul de profesori (raportul elev-profesor). În ceea ce privește datele, setul de date al școlii din California (CASchools) vine cu un pachet R numit AER, un acronim pentru Econometrie aplicată cu R (Kleiber și Zeileis 2020). După instalarea pachetului cu instalare.pachete („AER”) și atașându-l cu bibliotecă(AER) setul de date poate fi încărcat folosind funcția date ().

## # install the AER package (once)## install.packages("AER")## ## # load the AER packagelibrary(AER)# load the the data set in the workspacedata(CASchools)

odată ce un pachet a fost instalat, acesta este disponibil pentru utilizare în alte ocazii când este invocat cu library () – nu este nevoie să rulați install.pachete () din nou!

este interesant să știm cu ce fel de obiect avem de-a face.class() returnează clasa unui obiect. În funcție de clasa unui obiect, unele funcții (de exemplu plot() și rezumat()) se comportă diferit.

să verificăm clasa CASchools obiect.

class(CASchools)#> "data.frame"

se pare că CASchools este de date de clasă.cadru care este un format convenabil pentru a lucra cu, în special pentru efectuarea analizei de regresie.

cu ajutorul head() obținem o primă prezentare generală a datelor noastre. Această funcție afișează numai primele 6 rânduri ale setului de date care împiedică o ieșire supraaglomerată a consolei.

apăsați ctrl + L pentru a șterge consola. Această comandă șterge orice cod care a fost introdus și executat de dvs. sau tipărit în consolă prin funcțiile R. Vestea bună este că orice altceva este lăsat neatins. Nu pierdeți variabile definite etc. nici istoria codului. Este încă posibil să reamintim comenzile r executate anterior folosind tastele sus și jos. Dacă lucrați în RStudio, apăsați ctrl + sus pe tastatură (CMD + sus pe un Mac) pentru a examina o listă de comenzi introduse anterior.

head(CASchools)#> district school county grades students teachers#> 1 75119 Sunol Glen Unified Alameda KK-08 195 10.90#> 2 61499 Manzanita Elementary Butte KK-08 240 11.15#> 3 61549 Thermalito Union Elementary Butte KK-08 1550 82.90#> 4 61457 Golden Feather Union Elementary Butte KK-08 243 14.00#> 5 61523 Palermo Union Elementary Butte KK-08 1335 71.50#> 6 62042 Burrel Union Elementary Fresno KK-08 137 6.40#> calworks lunch computer expenditure income english read math#> 1 0.5102 2.0408 67 6384.911 22.690001 0.000000 691.6 690.0#> 2 15.4167 47.9167 101 5099.381 9.824000 4.583333 660.5 661.9#> 3 55.0323 76.3226 169 5501.955 8.978000 30.000002 636.3 650.9#> 4 36.4754 77.0492 85 7101.831 8.978000 0.000000 651.9 643.5#> 5 33.1086 78.4270 171 5235.988 9.080333 13.857677 641.8 639.9#> 6 12.3188 86.9565 25 5580.147 10.415000 12.408759 605.7 605.4

constatăm că setul de date constă din o mulțime de variabile și că majoritatea sunt numerice.

apropo: o alternativă la clasă() și cap() este str() care este dedus din ‘structură’ și oferă o imagine de ansamblu cuprinzătoare a obiectului. Încearcă!

revenind la CASchools, cele două variabile care ne interesează (adică., scorul mediu al testului și raportul elev-profesor) nu sunt incluse. Cu toate acestea, este posibil să se calculeze atât din datele furnizate. Pentru a obține raportul elev-profesor, împărțim pur și simplu numărul de elevi la numărul de profesori. Scorul mediu al testului este media aritmetică a scorului testului pentru citire și scorul testului de matematică. Următoarea bucată de cod arată modul în care cele două variabile pot fi construite ca vectori și modul în care acestea sunt anexate la CASchools.

# compute STR and append it to CASchoolsCASchools$STR <- CASchools$students/CASchools$teachers # compute TestScore and append it to CASchoolsCASchools$score <- (CASchools$read + CASchools$math)/2

dacă am fugit cap (CASchools) din nou, ne-ar găsi cele două variabile de interes ca coloane suplimentare numite STR și scor (verifica acest lucru!).

tabelul 4.1 din manual rezumă distribuția scorurilor testelor și a raporturilor elev-profesor. Există mai multe funcții care pot fi utilizate pentru a produce rezultate similare, de ex.,

mean () (calculează media aritmetică a numerelor furnizate),
sd () (calculează deviația standard a eșantionului),
quantile () (returnează un vector al cuantilelor eșantionului specificat pentru date).

următoarea bucată de cod arată cum să realizăm acest lucru. În primul rând, vom calcula statistici sumare pe coloanele STR și scorul de CASchools. Pentru a obține o ieșire frumoasă, adunăm măsurile într-o informație.cadru numit DistributionSummary.

# compute sample averages of STR and scoreavg_STR <- mean(CASchools$STR) avg_score <- mean(CASchools$score)# compute sample standard deviations of STR and scoresd_STR <- sd(CASchools$STR) sd_score <- sd(CASchools$score)# set up a vector of percentiles and compute the quantiles quantiles <- c(0.10, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9)quant_STR <- quantile(CASchools$STR, quantiles)quant_score <- quantile(CASchools$score, quantiles)# gather everything in a data.frame DistributionSummary <- data.frame(Average = c(avg_STR, avg_score), StandardDeviation = c(sd_STR, sd_score), quantile = rbind(quant_STR, quant_score))# print the summary to the consoleDistributionSummary#> Average StandardDeviation quantile.10. quantile.25. quantile.40.#> quant_STR 19.64043 1.891812 17.3486 18.58236 19.26618#> quant_score 654.15655 19.053347 630.3950 640.05000 649.06999#> quantile.50. quantile.60. quantile.75. quantile.90.#> quant_STR 19.72321 20.0783 20.87181 21.86741#> quant_score 654.45000 659.4000 666.66249 678.85999

în ceea ce privește datele eșantionului, folosim plot(). Acest lucru ne permite să detectăm caracteristicile datelor noastre, cum ar fi valorile aberante care sunt mai greu de descoperit uitându-ne la simple numere. De data aceasta adăugăm câteva argumente suplimentare la apelul plotului().

primul argument din apelul nostru de plot(), scor ~ STR, este din nou o formulă care afirmă variabile pe Y – și axa X. Cu toate acestea, de data aceasta cele două variabile nu sunt salvate în vectori separați, ci sunt coloane de CASchools. Prin urmare, R nu le-ar găsi fără ca datele argumentului să fie specificate corect. datele trebuie să fie în conformitate cu numele datelor.cadrul la care aparțin variabilele, în acest caz CASchools. Alte argumente sunt folosite pentru a schimba aspectul complotului: în timp ce main adaugă un titlu, xlab și ylab adaugă etichete personalizate la ambele axe.

plot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)")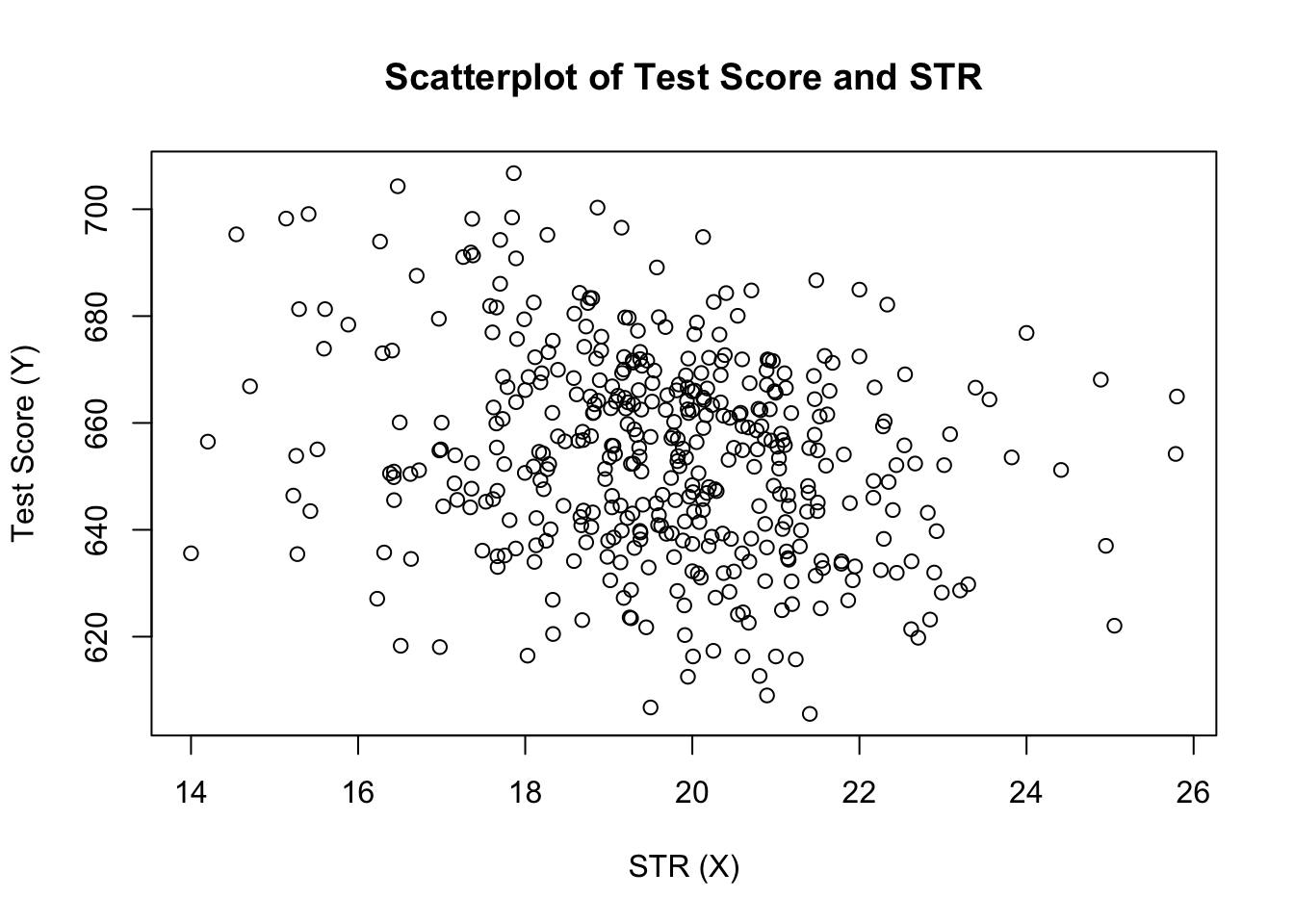

graficul (figura 4.2 din carte) arată scatterplot-ul tuturor observațiilor privind raportul elev-profesor și scorul testului. Vedem că punctele sunt puternic împrăștiate și că variabilele sunt corelate negativ. Adică, ne așteptăm să observăm scoruri mai mici la teste în clase mai mari.

funcția cor() (vezi ?cor pentru informații suplimentare) poate fi utilizat pentru a calcula corelația dintre doi vectori numerici.

cor(CASchools$STR, CASchools$score)#> -0.2263627

după cum sugerează deja scatterplot, corelația este negativă, dar destul de slabă.

sarcina cu care ne confruntăm acum este să găsim o linie care să se potrivească cel mai bine datelor. Desigur, am putea pur și simplu să rămânem cu inspecția grafică și analiza corelației și apoi să selectăm cea mai bună linie de montare prin ochi. Cu toate acestea, acest lucru ar fi destul de subiectiv: observatorii diferiți ar desena linii de regresie diferite. În acest sens, suntem interesați de tehnici mai puțin arbitrare. O astfel de tehnică este dată de estimarea obișnuită a celor mai mici pătrate (OLS).

Estimatorul ordinar al celor mai mici pătrate

Estimatorul OLS alege coeficienții de regresie astfel încât linia de regresie estimată să fie cât mai „apropiată” de punctele de date observate. Aici, apropierea este măsurată prin suma greșelilor pătrate făcute în prezicerea $Y$ dată $X$. Fie $b_0$ și $b_1$ unii estimatori ai $\beta_0$ și $\beta_1$. Apoi, suma greșelilor de estimare pătrată poate fi exprimată ca

Estimatorul OLS în modelul de regresie simplă este perechea de estimatori pentru interceptare și pantă care minimizează expresia de mai sus. Derivarea estimatorilor OLS pentru ambii parametri este prezentată în anexa 4.1 a cărții. Rezultatele sunt rezumate în conceptul cheie 4.2.

Estimatorul OLS, valorile prezise și reziduurile

estimatorii OLS ai pantei $\beta_1$ și interceptarea $\beta_0$ în modelul de regresie liniară simplă sunt\valorile prezise OLS $\widehat{Y}_i$ și reziduurile $\hat{u}_i$ sunt\

interceptarea estimată $\hat{\beta}_0$, parametrul pantei $\hat{\Beta}_1$ și reziduurile $\Left(\Hat{U}_i\right)$ sunt calculate dintr-un eșantion de $n$ observații ale $x_i$ și $y_i$, $i$, $…\ ), \(n$. Acestea sunt estimări ale interceptării populației necunoscute $\stânga (\beta_0 \ dreapta)$, panta $\stânga (\beta_1\ dreapta)$ și termenul de eroare$(u_i)$.

formulele prezentate mai sus pot să nu fie foarte intuitive la prima vedere. Următoarea aplicație interactivă își propune să vă ajute să înțelegeți mecanica OLS. Puteți adăuga observații făcând clic pe sistemul de coordonate în care datele sunt reprezentate de puncte. Odată ce două sau mai multe observații sunt disponibile, Aplicația calculează o linie de regresie folosind OLS și unele statistici care sunt afișate în panoul din dreapta. Rezultatele sunt actualizate pe măsură ce adăugați observații suplimentare la panoul din stânga. Un dublu clic resetează aplicația, adică toate datele sunt eliminate.

există multe modalități posibile de a calcula $\hat{\beta}_0$ și $\hat{\beta}_1$ în R. De exemplu, am putea implementa formulele prezentate în conceptul cheie 4.2 cu două dintre funcțiile cele mai de bază ale lui R: mean() și sum(). Înainte de a face acest lucru, atașăm setul de date CASchools.

attach(CASchools) # allows to use the variables contained in CASchools directly# compute beta_1_hatbeta_1 <- sum((STR - mean(STR)) * (score - mean(score))) / sum((STR - mean(STR))^2)# compute beta_0_hatbeta_0 <- mean(score) - beta_1 * mean(STR)# print the results to the consolebeta_1#> -2.279808beta_0#> 698.9329

apelarea attach (CASchools) ne permite să adresăm o variabilă conținută în CASchools după numele său: nu mai este necesar să utilizați operatorul $ împreună cu setul de date: R poate evalua direct numele variabilei.

r folosește obiectul în mediul utilizator dacă acest obiect împărtășește numele variabilei conținute într-o bază de date atașată. Cu toate acestea, este o practică mai bună să folosiți întotdeauna nume distinctive pentru a evita astfel de ambivalențe (aparent)!

observați că adresăm variabilele conținute în setul de date atașat CASchools direct pentru restul acestui capitol!

desigur, există și mai multe modalități manuale de a îndeplini aceste sarcini. OLS fiind una dintre cele mai utilizate tehnici de estimare, R conține, desigur, deja o funcție încorporată numită lm() (model liniar) care poate fi utilizată pentru a efectua analiza de regresie.

primul argument al funcției care trebuie specificată este, similar cu plot(), formula de regresie cu sintaxa de bază y ~ x unde y este variabila dependentă și x variabila explicativă. Datele argument determină setul de date care urmează să fie utilizat în regresie. Acum revizuim exemplul din cartea în care este analizată relația dintre scorurile testului și dimensiunile clasei. Următorul cod folosește lm () pentru a reproduce rezultatele prezentate în figura 4.3 a cărții.

# estimate the model and assign the result to linear_modellinear_model <- lm(score ~ STR, data = CASchools)# print the standard output of the estimated lm object to the console linear_model#> #> Call:#> lm(formula = score ~ STR, data = CASchools)#> #> Coefficients:#> (Intercept) STR #> 698.93 -2.28

să adăugăm linia de regresie estimată la complot. De data aceasta mărim și intervalele ambelor axe setând argumentele xlim și ylim.

# plot the dataplot(score ~ STR, data = CASchools, main = "Scatterplot of TestScore and STR", xlab = "STR (X)", ylab = "Test Score (Y)", xlim = c(10, 30), ylim = c(600, 720))# add the regression lineabline(linear_model)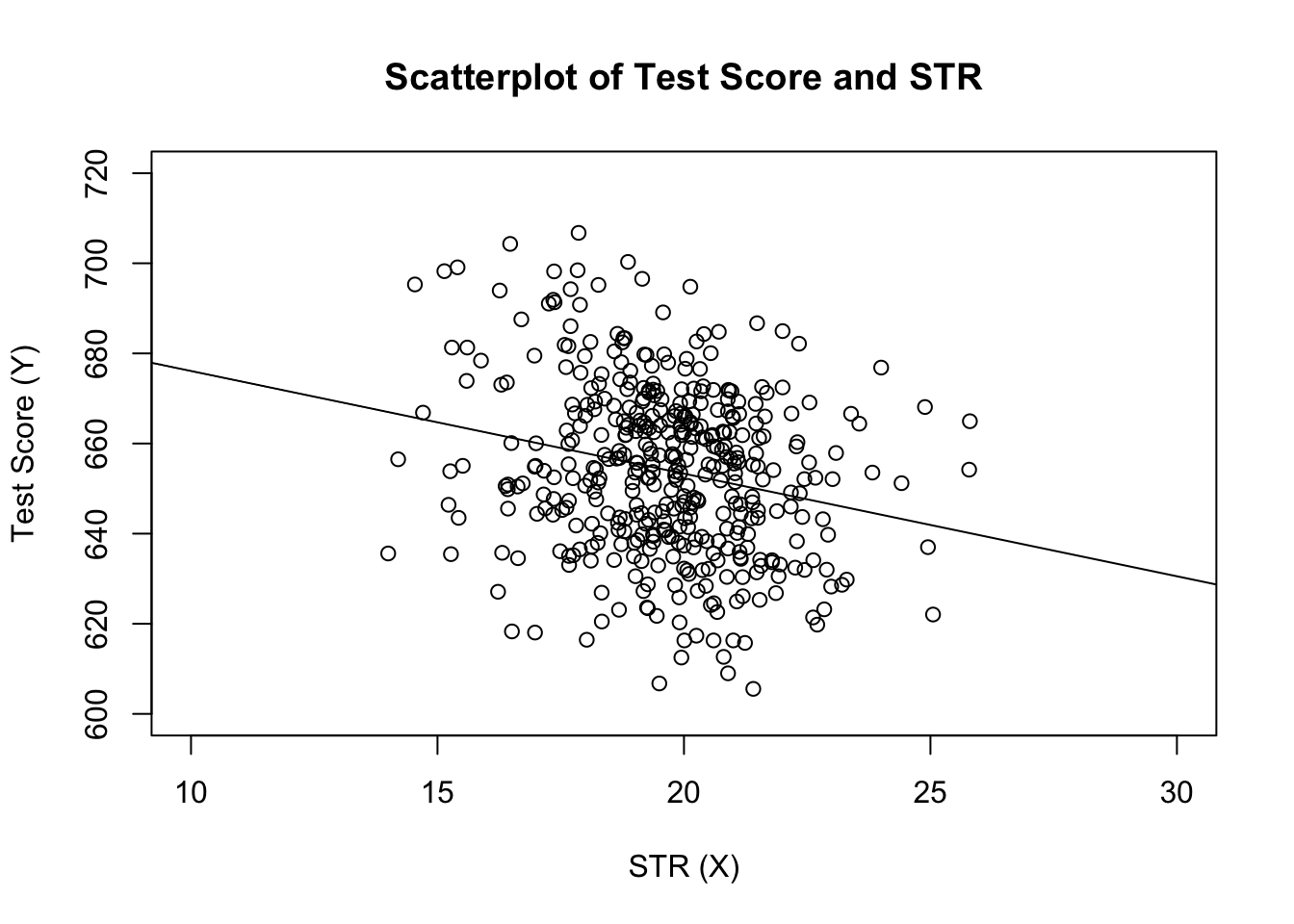

ai observat că de data asta, nu am trecut parametrii de interceptare și pantă către abline? Dacă apelați abline () pe un obiect din clasa lm care conține doar un singur regresor, r desenează automat linia de regresie!