catamorfismul pentru oricare este o generalizare a pliului său. Catamorfismul permite operațiuni care nu sunt disponibile prin fold.
acest articol face parte dintr-o serie de articole despre catamorfisme. Un catamorfism este o abstracție universală care descrie modul de digerare a unei structuri de date într-o valoare potențial mai compactă.
acest articol prezintă catamorfismul pentru oricare (cunoscut și sub numele de rezultat), precum și modul de identificare a acestuia. Începutul acestui articol prezintă catamorfismul în C#, cu exemple. Restul articolului descrie modul de deducere a catamorfismului. Această parte a articolului prezintă munca mea în Haskell. Cititorii care nu se simt confortabil cu Haskell pot citi doar prima parte și pot considera restul articolului ca o anexă opțională.
fie este un container de date care modelează două rezultate care se exclud reciproc. Este adesea folosit pentru a returna valori care pot fi corecte (dreapta) sau incorecte (stânga). În programarea funcțională tastată static, cu preferință pentru funcțiile totale, fie oferă o modalitate mai sănătoasă, mai rezonabilă de a modela rezultatele succesului și erorilor decât aruncarea excepțiilor.
c# catamorfism #
acest articol folosește codificarea Bisericii a oricăreia dintre ele. Catamorfismul pentru oricare dintre ele este metoda Match :
T Match<T>(Func<L, T> onLeft, Func<R, T> onRight);
până la acest articol, toate catamorfismele anterioare au fost o pereche realizată dintr-o valoare inițială și o funcție. Catamorfismul este o generalizare, deoarece este o pereche de funcții. O funcție gestionează cazul în care există o valoare stângă, iar cealaltă funcție gestionează cazul în care există o valoare corectă. Ambele funcții trebuie să returneze același tip unificator, care este adesea un șir sau ceva similar care poate fi afișat într-o interfață de utilizator:
> IEither<TimeSpan, int> e = new Left<TimeSpan, int>(TimeSpan.FromMinutes(3));> e.Match(ts => ts.ToString(), i => i.ToString())"00:03:00"> IEither<TimeSpan, int> e = new Right<TimeSpan, int>(42);> e.Match(ts => ts.ToString(), i => i.ToString())"42"
veți vedea adesea exemple precum cele de mai sus care transformă atât cazurile din stânga, cât și cele din dreapta în șiruri sau ceva care poate fi reprezentat ca un tip de răspuns unificator, dar acest lucru nu este în niciun fel necesar. Dacă puteți veni cu un tip unificator, puteți converti ambele cazuri la acel tip:
> IEither<Guid, string> e = new Left<Guid, string>(Guid.NewGuid());> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)12> IEither<Guid, string> e = new Right<Guid, string>("foo");> e.Match(g => g.ToString().Count(c => 'a' <= c), s => s.Length)3
în cele două exemple de mai sus, utilizați două funcții diferite care reduc valorile Guid și string la un număr. Funcția care transformă valorile Guid într-un număr contează câte dintre cifrele hexazecimale sunt mai mari sau egale cu A (10). Cealaltă funcție returnează pur și simplu lungimea string, dacă este acolo. Acest exemplu nu are sens, dar metodei Match nu-i pasă de asta.
în utilizarea practică, fie este adesea folosit pentru tratarea erorilor. Articolul despre codificarea Bisericii conține un exemplu.
fie F-Algebra #
ca în articolul precedent, voi folosi Fix și cata așa cum se explică în articolul excelent al lui Bartosz Milewski despre F-algebre.
în timp ce F-algebrele și punctele fixe sunt utilizate mai ales pentru structurile de date recursive, puteți defini și o f-algebră pentru o structură de date nerecursivă. Ați văzut deja un exemplu în articolele despre Catamorfismul Boolean și poate catamorfismul. Diferența dintre, De exemplu, poate valori și oricare este că ambele cazuri ale fiecăruia poartă o valoare. Puteți modela acest lucru ca Functor atât cu un tip de operator de transport, cât și cu două argumente de tip pentru datele care pot conține:
data EitherF l r c = LeftF l | RightF r deriving (Show, Eq, Read) instance Functor (EitherF l r) where fmap _ (LeftF l) = LeftF l fmap _ (RightF r) = RightF r
am ales să numesc ‘tipuri de date’ l (pentru stânga) și r (pentru dreapta) și tipul de operator c (pentru operator). Așa cum a fost și cazul BoolF și MaybeF, instanța Functor ignoră funcția map, deoarece tipul de purtător lipsește atât din cazul LeftF, cât și din cazul RightF. La fel ca instanțele Functor pentru BoolF și MaybeF, s-ar părea că nu se întâmplă nimic, dar la nivel de tip, aceasta este încă o traducere de la EitherF l r c la EitherF l r c1. Nu de mult de o funcție, poate, dar cu siguranta un endofunctor.
așa cum s-a întâmplat și la deducerea catamorfismelor poate și Listă, Haskell nu este prea mulțumit de definirea instanțelor pentru un tip precum Fix (EitherF l r). Pentru a rezolva această problemă, puteți introduce un înveliș newtype :
newtype EitherFix l r = EitherFix { unEitherFix :: Fix (EitherF l r) } deriving (Show, Eq, Read)
puteți defini Functor, Applicative, Monad, etc. instanțe pentru acest tip fără a recurge la extensii GHC funky. Rețineți că, în cele din urmă, scopul acestui cod este doar să vă dați seama cum arată catamorfismul. Acest cod nu este destinat utilizării reale.
o pereche de funcții de ajutor facilitează definirea valorilor EitherFix :
leftF :: l -> EitherFix l rleftF = EitherFix . Fix . LeftF rightF :: r -> EitherFix l rrightF = EitherFix . Fix . RightF
cu aceste funcții, puteți crea EitherFix valori:
Prelude Data.UUID Data.UUID.V4 Fix Either> leftF <$> nextRandomEitherFix {unEitherFix = Fix (LeftF e65378c2-0d6e-47e0-8bcb-7cc29d185fad)}Prelude Data.UUID Data.UUID.V4 Fix Either> rightF "foo"EitherFix {unEitherFix = Fix (RightF "foo")}
asta e tot ce ai nevoie pentru a identifica catamorfismul.
Haskell catamorfism #
în acest moment, aveți două din cele trei elemente ale unei F-algebră. Aveți un endofunctor (EitherF l r) și un obiect c, dar tot trebuie să găsiți un morfism EitherF l r c -> c. Observați că algebra pe care trebuie să o găsiți este funcția care reduce functor la tipul său de purtător c, Nu ‘tipuri de date’ l și r. Acest lucru durează ceva timp pentru a vă obișnui, dar așa funcționează catamorfismele. Acest lucru nu înseamnă, totuși, că veți ajunge să ignorați l și r, după cum veți vedea.
ca și în articolele anterioare, începeți prin a scrie o funcție care va deveni catamorfismul, bazat pe cata:
eitherF = cata alg . unEitherFix where alg (LeftF l) = undefined alg (RightF r) = undefined
în timp ce acest compilează, cu implementările sale undefined, evident că nu face nimic util. Mi se pare, totuși, că mă ajută să gândesc. Cum puteți returna o valoare de tipul c din cazul LeftF? Puteți transmite un argument funcției eitherF :
eitherF fl = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = undefined
în timp ce ați putea, din punct de vedere tehnic, să transmiteți un argument de tipul c la eitherF și apoi să returnați acea valoare din cazul LeftF, asta ar însemna că ați ignora valoarea l. Acest lucru ar fi incorect, deci, în schimb, faceți argumentul o funcție și apelați-l cu l. De asemenea, puteți trata cazul RightF în același mod:
eitherF :: (l -> c) -> (r -> c) -> EitherFix l r -> ceitherF fl fr = cata alg . unEitherFix where alg (LeftF l) = fl l alg (RightF r) = fr r
acest lucru funcționează. Deoarece cata are tipul Functor f => (f a -> a) -> Fix f -> a, asta înseamnă că algare tipul f a -> a. În cazul EitherF, compilatorul deduce că funcția alg are tipul EitherF l r c -> c, care este exact ceea ce aveți nevoie!
acum Puteți vedea pentru ce este tipul de transport c. Este tipul pe care algebra îl extrage și, prin urmare, tipul pe care îl returnează catamorfismul.
acesta este catamorfismul pentru oricare dintre ele. Așa cum a fost consecvent până acum, este o pereche, dar acum făcută din două funcții. După cum ați văzut în mod repetat, acesta nu este singurul catamorfism posibil, deoarece puteți, de exemplu, să răsturnați banal argumentele la eitherF.
am ales reprezentarea prezentată aici deoarece este izomorfă pentru funcția either din modulul încorporat Data.Either al lui Haskell, care numește funcția „analiza cazului pentru tipul Either„. Ambele funcții (eitherF și either) sunt echivalente cu metoda c# Match de mai sus.
Basis #
puteți implementa cele mai multe alte funcționalități utile cu eitherF. Iată instanța Bifunctor :
instance Bifunctor EitherFix where bimap f s = eitherF (leftF . f) (rightF . s)
din această instanță, instanța Functor urmează trivial:
instance Functor (EitherFix l) where fmap = second
pe partea de sus a Functor puteți adăuga Applicative:
instance Applicative (EitherFix l) where pure = rightF f <*> x = eitherF leftF (<$> x) f
observați că implementarea <*> este similară cu implementarea <*> pentru MaybeFix. Același lucru este cazul pentru Monad instanță:
instance Monad (EitherFix l) where x >>= f = eitherF leftF f x
nu numai că este EitherFix Foldable, este Bifoldable:
instance Bifoldable EitherFix where bifoldMap = eitherF
observați, interesant, că bifoldMapeste identic cu eitherF.
instanța Bifoldable vă permite să implementați banal instanța Foldable :
instance Foldable (EitherFix l) where foldMap = bifoldMap mempty
puteți găsi prezența mempty încurcată, deoarece bifoldMap (sau eitherF; sunt identice) ia ca argumente două funcții. Este mempty o funcție?
Da, mempty poate fi o funcție. Aici, este. Există o instanță Monoid pentru orice funcție a -> m, unde m este o instanță Monoid și mempty este identitatea pentru acel monoid. Acesta este exemplul folosit aici.
la fel cum EitherFix este Bifoldable, este de asemenea Bitraversable:
instance Bitraversable EitherFix where bitraverse fl fr = eitherF (fmap leftF . fl) (fmap rightF . fr)
puteți implementa confortabil instanța Traversable bazată pe instanța Bitraversable :
instance Traversable (EitherFix l) where sequenceA = bisequenceA . first pure
în cele din urmă, puteți implementa conversii la și de la tipul standard Either, folosind ana ca dual de cata:
toEither :: EitherFix l r -> Either l rtoEither = eitherF Left Right fromEither :: Either a b -> EitherFix a bfromEither = EitherFix . ana coalg where coalg (Left l) = LeftF l coalg (Right r) = RightF r
acest lucru demonstrează că EitherFix este izomorf la Either, ceea ce stabilește din nou că eitherF și either sunt echivalente.
relații #
în această serie, ați văzut diverse exemple de catamorfisme ale structurilor care nu au pliuri, catamorfisme care coincid cu pliurile și acum un catamorfism care este mai general decât pliul. Introducerea seriei a inclus această diagramă:
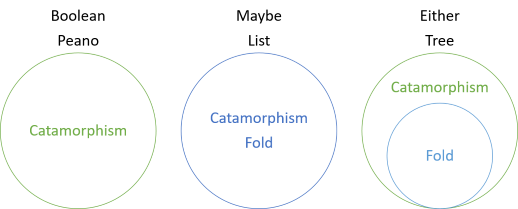
aceasta arată că valorile booleene și numerele Peano au catamorfisme, dar fără pliuri, în timp ce Pentru poate și Listă, pliul și catamorfismul sunt aceleași. Cu toate acestea, pentru oricare dintre ele, pliul este un caz special al catamorfismului. Ori pentru oricare ‘pretinde’ că partea stângă nu există. În schimb, valoarea stângă este interpretată ca o valoare dreaptă lipsă. Astfel, pentru a plia oricare dintre valori, trebuie să furnizați o valoare ‘rezervă’ care va fi utilizată în cazul în care o valoare fie nu este o valoare corectă:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> foldr (const . show) "" e""
într-o sesiune GHCi ca cele de mai sus, puteți crea două valori de același tip. Cazul din dreapta este o valoare Ordering, în timp ce cazul din stânga este o valoare Integer.
cu foldr, nu există nici o modalitate de a accesa cazul din stânga. În timp ce puteți accesa și transforma valoarea Ordering corectă, numărul 42 este pur și simplu ignorat în timpul fold-ului. În schimb, valoarea implicită "" este returnată.
contrastează acest lucru cu catamorfismul, care poate accesa ambele cazuri:
Prelude Fix Either> e = rightF LT :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"LT"Prelude Fix Either> e = leftF 42 :: EitherFix Integer OrderingPrelude Fix Either> eitherF show show e"42"
într-o sesiune ca aceasta, recreezi aceleași valori, dar folosind catamorfismul eitherF, acum poți accesa și transforma atât cazurile din stânga, cât și cele din dreapta. Cu alte cuvinte, catamorfismul vă permite să efectuați operații care nu sunt posibile cu pliul.
este interesant, totuși, să observăm că în timp ce pliul este o specializare a catamorfismului, bifoldul este identic cu catamorfismul.
rezumat #
catamorfismul pentru oricare dintre ele este o pereche de funcții. O funcție transformă cazul din stânga, în timp ce cealaltă funcție transformă cazul din dreapta. Pentru orice valoare, va fi utilizată doar una dintre aceste funcții.
când am întâlnit inițial conceptul de catamorfism, mi-a fost greu să disting între catamorfism și pliu. Problema mea a fost, cred, că tutorialele pe care le-am întâlnit au folosit mai ales liste legate pentru a demonstra cum, în acest caz, pliul este catamorfismul. Se pare, totuși, că acest lucru nu este întotdeauna cazul. Un catamorfism este o abstractizare generală. O pliere, pe de altă parte, mi se pare a fi în mare parte legată de colecții.
în acest articol ați văzut primul exemplu de catamorfism care poate face mai mult decât pliul. Pentru oricare, pliul este doar un caz special al catamorfismului. De asemenea, ați văzut, totuși, cum catamorfismul era identic cu bifoldul. Astfel, nu este încă clar cum se raportează aceste concepte. Prin urmare, în articolul următor, veți obține un exemplu de container în care nu există bifold și unde catamorfismul este, într-adevăr, o generalizare a pliului.
următor: Catamorfism copac.